博客作业05--查找
一.学习总结(2分)
1.1查找的思维导图
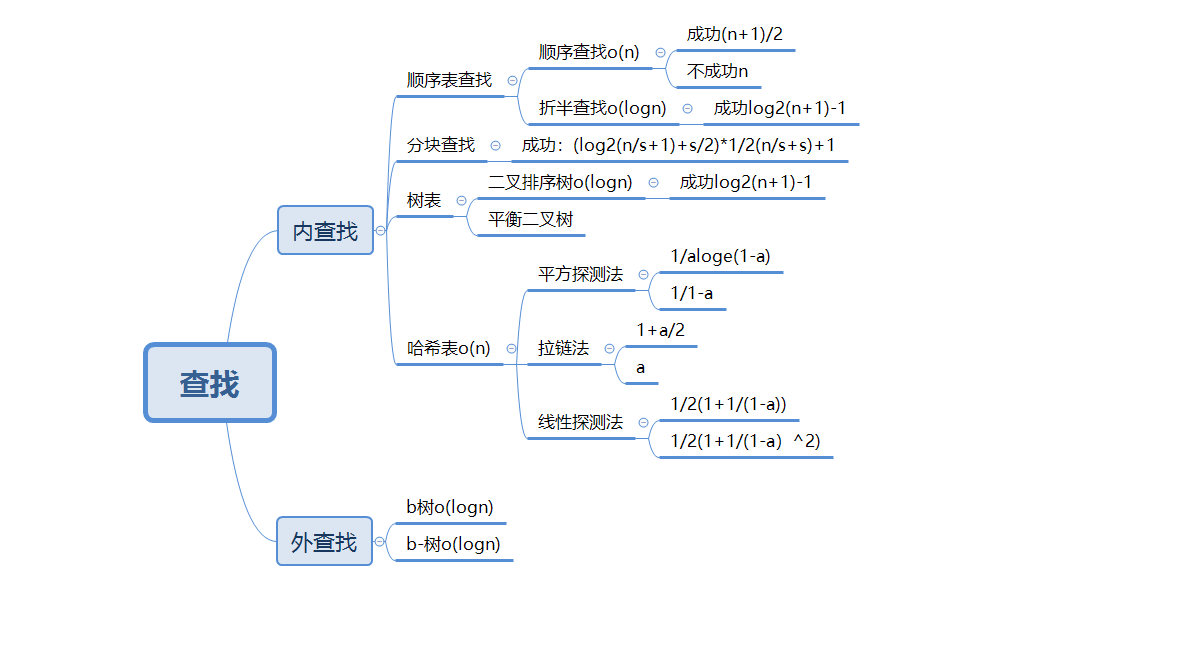
1.2 查找学习体会
查找大概可以分为按照地址查找和按照数值查找
顺序表查找这里面包含了一种极为重要的二分查找的思路。而这种顺序表查找就是按照数值查找的一种
分块查找:把数据分成不同的块,块下面对应着信息。这种思路就是按址查找的,而先查数据属于哪一个快也是运用到二分法的思路。
数表查找:是把二分法升级的一种查找方法其算法思路上沿用二分查找无非是换了一种更为直观的存储方式
哈希表:按照数值查找的一种数据结构,使得数值的存储更为密集,这有利于查找效率的提高和存储空间的节约。
b树,b-树:avl树的升级可称为多差平衡树适合大量文本信息的存储查找
二.PTA实验作业(4分)
6-3 二叉搜索树中的最近公共祖先
1 设计思路(伪代码或流程图)
//a为节点的值,small和big分别是较小和较大的数
查找树中是否有这两个数
if(都找的到){
while(1){
if(small<a<big)返回这个节点的值;
if(a的左孩子或者右孩是small或者big)返回这个节点的值
else if(a<small)往右子树查
else if(a>big)往左子树查
}
}
else 返回-1
2.代码截图
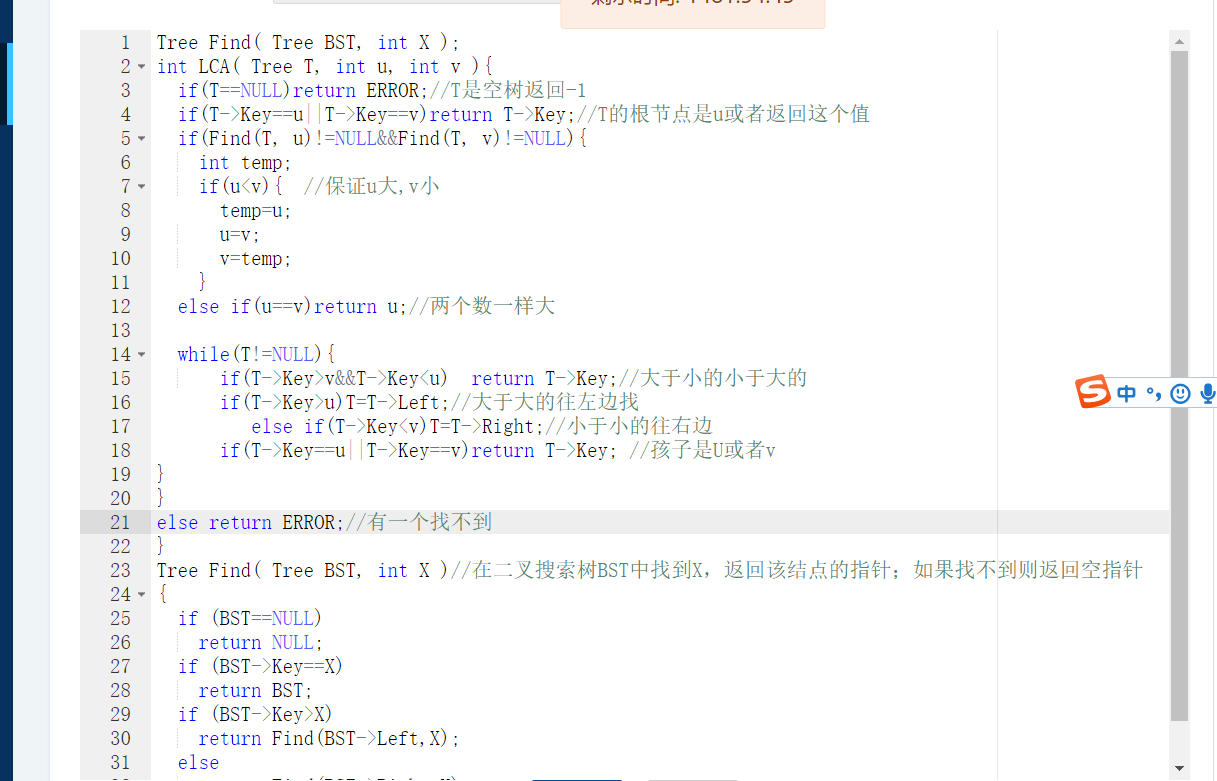
忽略了很多特殊情况比如说这两个数值一样大啊有一个数值是根节点啊这种情况后冷静分析改过
3.PTA提交列表说明

7-1 QQ帐户的申请与登陆
1 设计思路(伪代码或流程图)
//定义映射函数用QQ号对应映射密码
将账号Longlong型用Map容器映射到密码上
调用map的迭代器:查找map里面的是否有这个账号
if(op=='L')
{
if(匹配账号){//调用mapfind函数
if(密码匹配) 登录成功
else if(密码不存在)密码错误
}
else if输出账号不存在
}
else if(op=='N'){
if(账号存在)匹配密码完成映射//调用map。insert函数
else 输出账号已存在
}
2.代码截图
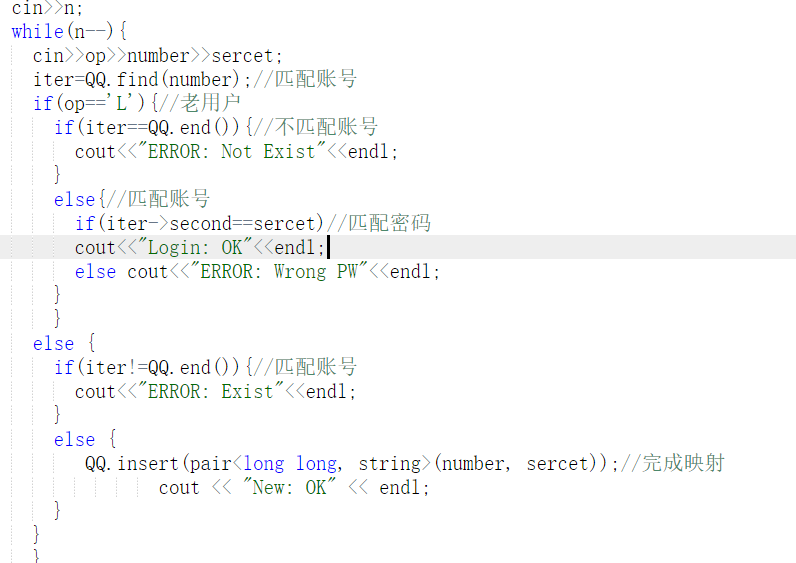
3.PTA提交列表说明

6-2 是否二叉搜索树
1 设计思路(伪代码或流程图)
if (T==NULL)return true;
if(T->Left!=NULL&&T->data大于左树最大值)return false;
if(T->Right!=NULL&&右树最小值<T->Data)return false;
递归判断左树和右树
2.代码截图
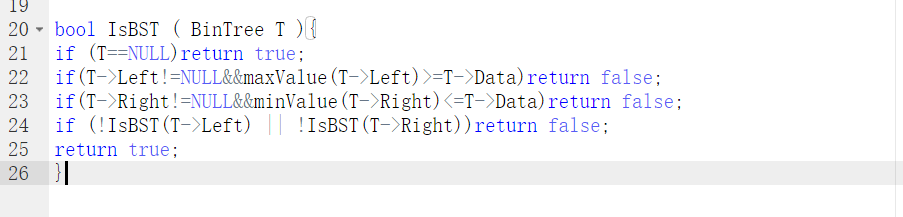
3.TA提交列表说明

只判断左孩右孩没判断左树右树
三.截图本周题目集的PTA最后排名(3分)
3.1 PTA排名

3.3 我的总分:125
四. 阅读代码(必做,1分)
路由器中的SPF算法查找最短路径及路由表完善
一、选定根节点;//----不管以哪个节点为根节点,最后计算出的生成树应该是一样的(即每个节点到其他节点的权值不变)
二、遍历该选定节点的所有直连节点。遍历过程中,若根与某节点的分支为
l 新分支,则添加该分支到分支列表,并记录分支的权重、根的下一跳;
l 已存在于分支列表,则与分支列表中已存在分支的权重值比较优劣,并把较优值更新到分支列表中;
l 已存在于权重列表,则忽略;
三、把分支列表中的最优分支移出至权重列表,并选定该分支的节点;
四、若分支列表非空,则继续步骤三;否则算法结束。
算法结束后,权重列表即为最短路径树,用于生成路由表或其它后续工作。
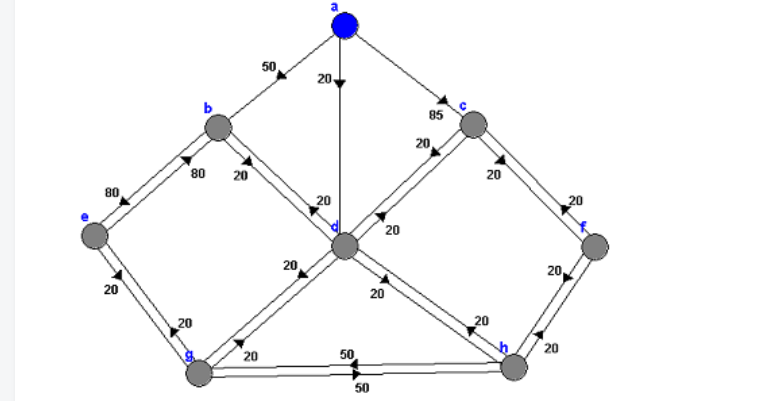
下面举个简单例子,箭头方向为节点配置链路权重(metric),注意权重是单向的,修改权重一般情况下要确保两端一致。a为运行SPF算法的节点,LSDB已收敛:
*下述显示含义为节点(下一跳) 权重
一、SPF把a、b、c、d、e、f、g、h置为未遍历状态,并以本节点(R1)为根。添加a(a)到权重列表,权重为0,下一跳为a。接着遍历a的直连节点b、c、d,并把b(b) 50,c(c) 85,d(d) 20添加到分支列表。其中d(d)的权重最优,为20。添加d(d)到权重列表,权重为20,下一跳为d,并选定d;
二、遍历d所有连接的节点。这里d-b 20,d-c 20,d-g 20,d-h 20。分支列表中b(b)从50改为40,下一跳改为d;c(c)从85改为40,下一跳改为d;添加g(d) 40,h(d) 40。这时分支列表包含:b(d) 40,c(d) 40,g(d) 40,h(d) 40。添加b(d)到权重列表,权重为40,下一跳为d,并选定b;
三、遍历b所有连接的节点。这里分支为b-e 80,b-d 20,由于d已以被添加到权重列表,不再考虑。分支列表中添加e(d) 120。这时分支列表包含:c(d) 40,g(d) 40,h(d) 40,e(d) 120。添加c(d)到权重列表,权重为40,下一跳为d,并选定c;
四、遍历c。这里分支为c-f 20,c-d 20,由于d已被添加到权重列表,不再考虑。分支列表添加f(d) 60。这时分支列表包含:g(d) 40,h(d) 40,e(d) 120,f(d) 60。添加g(d) 到权重列表,权重为40,下一跳为d,并选定g;
五、遍历g。g分支为g-e 20,g-h 50。分支列表修改e(d) 60。这时分支列表包含:h(d) 40,e(d) 60,f(d) 60。添加h(d)到权重列表,权重为40,下一跳为d,并选定h;
六、遍历h。h分支为h-g 50,h-f 20。g已被添加到权重列表,不考虑;而a-d-c-f和a-d-h-f同为60,下一跳同为d,该新分支与分支列表中的分支并无差异。这时分支列表包含:e(d) 60,f(d) 60。添加e(d)到权重列表,权重为60,下一跳为d,并选定e;
七、遍历e。分支为e-b 80,e-g 20,由于b、g已在权重列表,分支列表无需改变,为f(d) 60。添加f(d)到权重列表,权重为60,下一跳为d。
八、由于分支列表为空,因此SPF算法结束。这时权重列表为:

//
算法中运用到了大量的遍历程序这里可以运用到我们所学的顺序表遍历的方式,而且这种数据库的存储结构应该是动态的比较想用的话应该是vector数组或者是链表,个人觉得vector数组比较优秀因为它有一个选最优的过程可以调用库函数sort()这就大大减少了麻烦,也可以用set函数做一个路由节点的集合。
但是好像用我们学的图的逻辑结构会更简单(知识有限),图结构里面的最小生成树应该对支持这个算法有很大作用。
五. 代码Git提交记录截图





