博客作业04--树
一.学习总结(2分)
1.1树结构思维导图
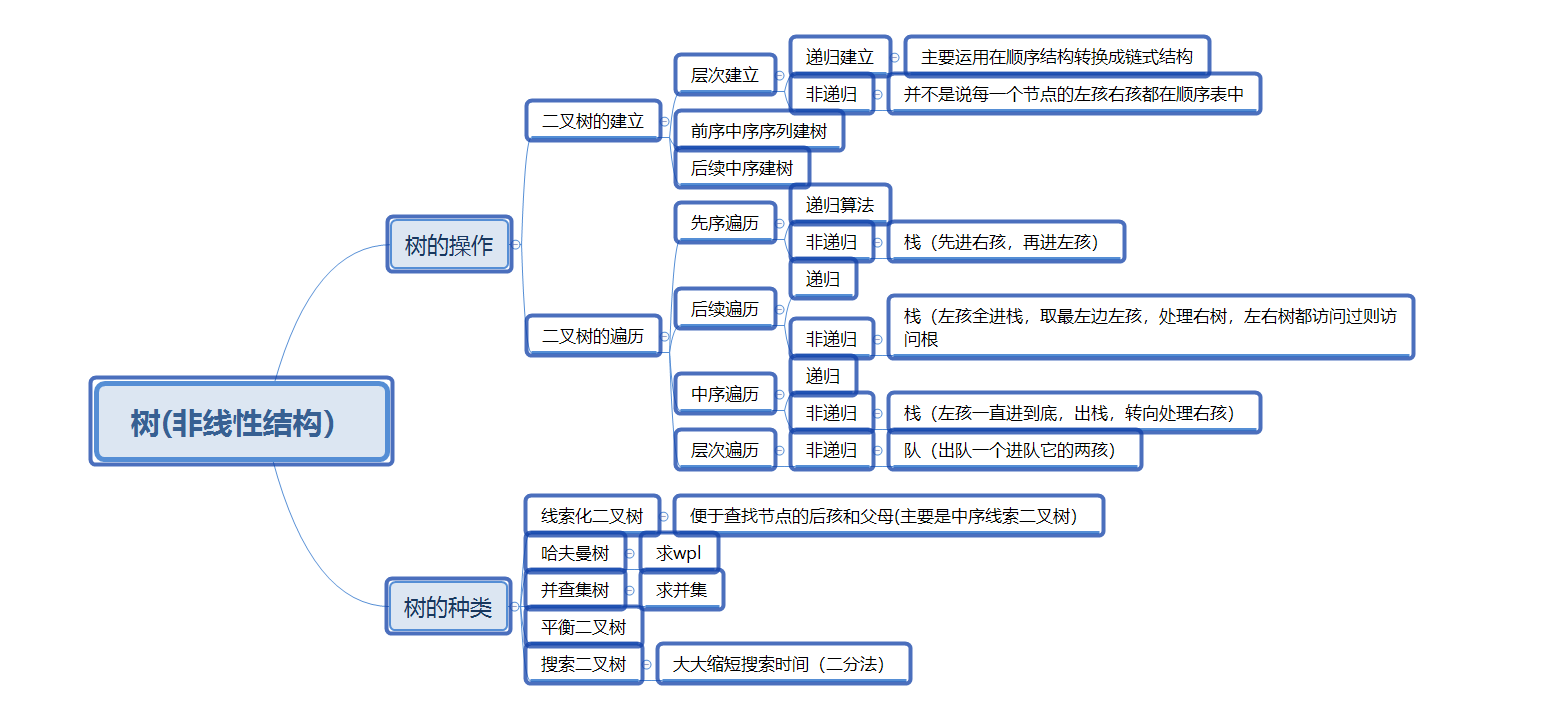
1.2 树结构学习体会
树的前中后序递归操作的访问路径都如下图
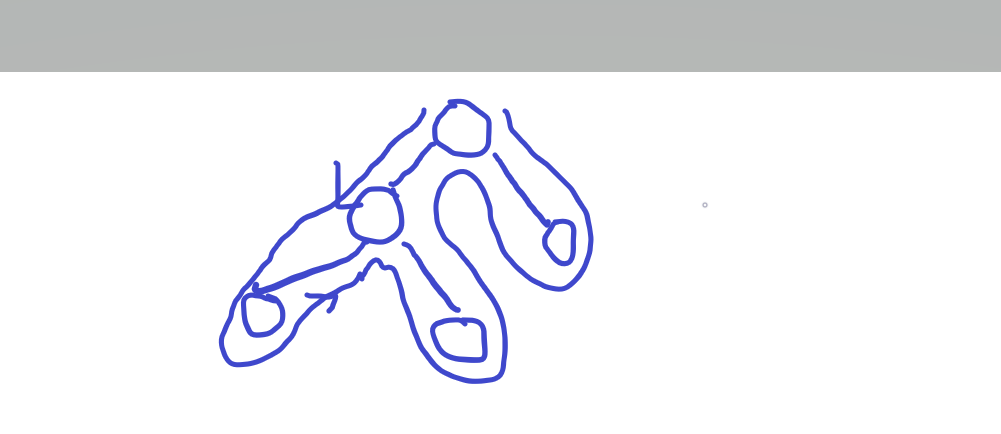
树的层次遍历的路径则如下图
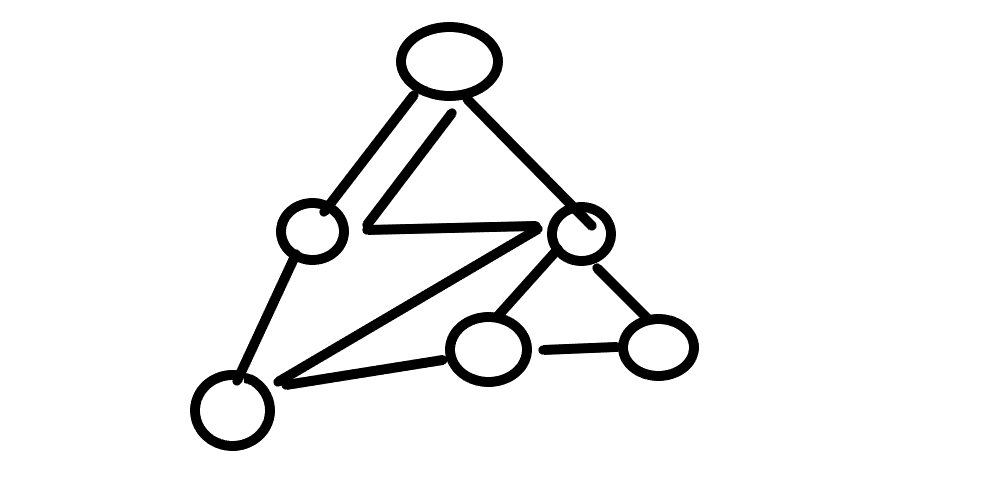
操作{
进队第一个节点,
while(队不空)
{
访问该节点,
if(BT->lchild!=NULL)进队。
if(BT->rchild!=NULL)进队。
}
}
三序遍历的非递归(先序为例):
操作:{
进栈树的根节点;
while(栈不空){
访问之
if(BT->rchild!=NULL)进栈。
if(BT->lchild!=NULL)进栈。
}
}
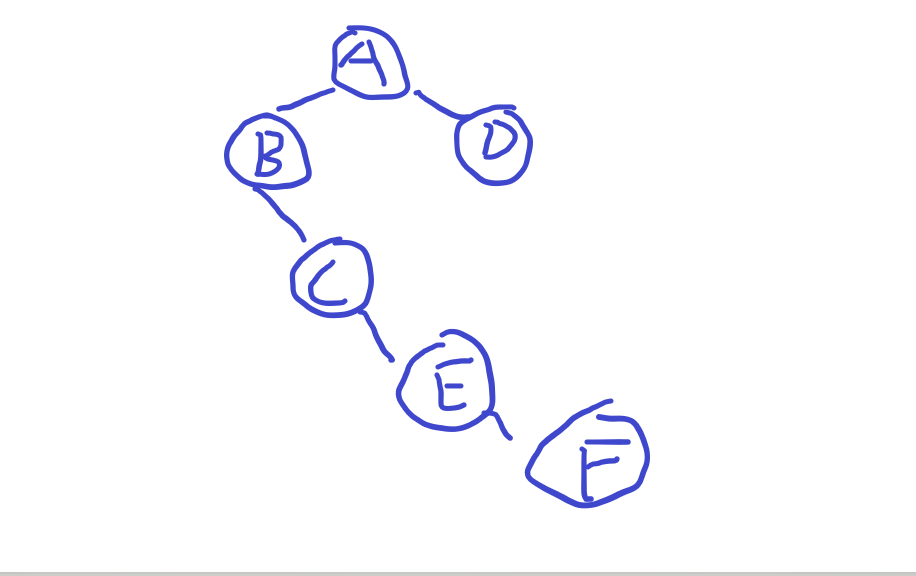
前序中序建树过程:
前:ABCEFD
中:BCEFAD
前序的第一个A:说明它是根节点
左前树: BCEF 左中:BCEF
右前树: D 右中:D
重复找左右树。
结果如下图
哈夫曼树
如1357建树:
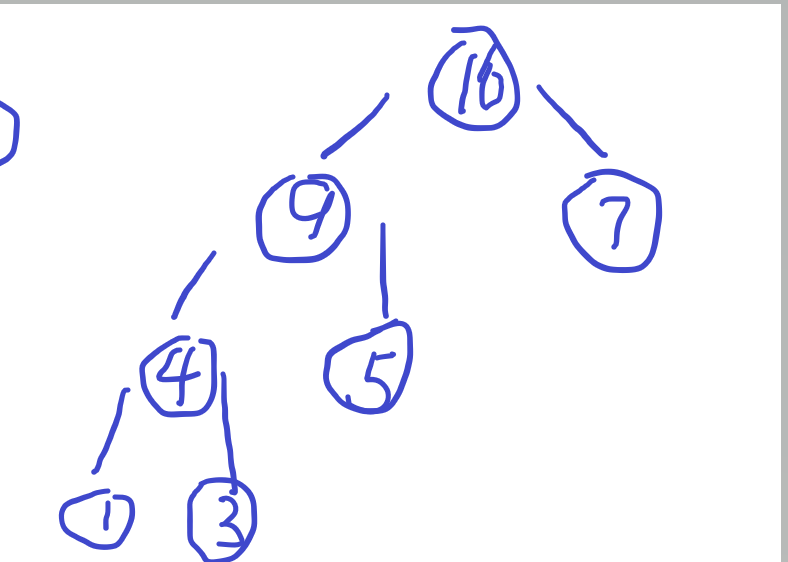
细心观察会发现其wpl与非叶子节点的和是相等的
数学证明:设 a b c d e 几个节点建立哈夫曼树(假设每一个节点都比后加进来的节点大)
a+b为第一个非根节点 则a+b+c为第二个依次类推
会发现非叶子节点的和是e+2d+3c+4b+4a
而wpl也恰好是这个值
并非偶然这可以从哈夫曼树的结构来考虑因为每递加一层已经建立过的节点就加1比方说哈夫曼树有三层那么最下面一层的和会在第二层次中被加也会在第一层被加也就是被
了两次与wpl构造数的算法完全一致。于是可运用贪心算法快速得到wpl。
树是一种非线性结构
树形结构不但本身很有用,还反映了许多计算过程的抽象结构;
树形结构的结点形成一种层次结构;
递归则是它的重点,但递归这种操作理解起来的难度真的很大,因此要多看看别人的代码来学习。
二.PTA实验作业(4分)
2.1 题目1:修理牧场
1 设计思路(伪代码或流程图)
定义一个队列可以让进队元素按从大到小排列
for(i=0;i<N;I++){
依次输入每一个数
并且入队
}
while(队不空){
出队两个元素ab
并让total=a+b;
再进队两个元素。
}
输出结果
2.代码截图
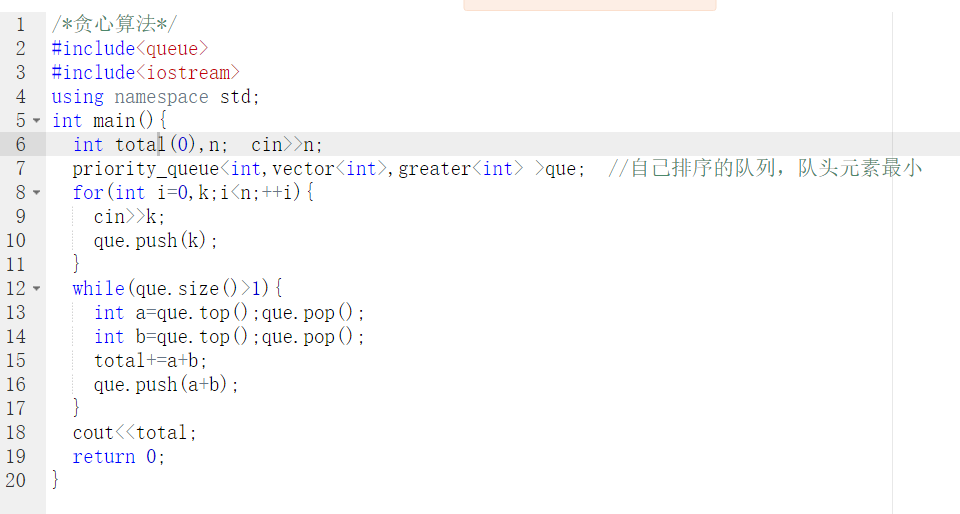
3.PTA提交列表说明

2.1 题目2:朋友圈
1 设计思路(伪代码或流程图)
//定义三个数组一个是保留每一个每一个数对应的根节点一个保留所有根节点
//最后一个保留每一个根对应的孩子数
初始化树中的每个节点数值为-1
先输入孩子数和朋友圈数n,m
for(int i=0;i<m;i++){
输入每个朋友圈中人的个数
并且保留它们的根节点
并且记录每个下标对应的根节点
当这个根是其它根的孩子则将这个朋友圈的其他人的根都转成这个跟
}
遍历保留每个节点根的数组记录总数在最后一个数组中
遍历取最大值
2.代码截图
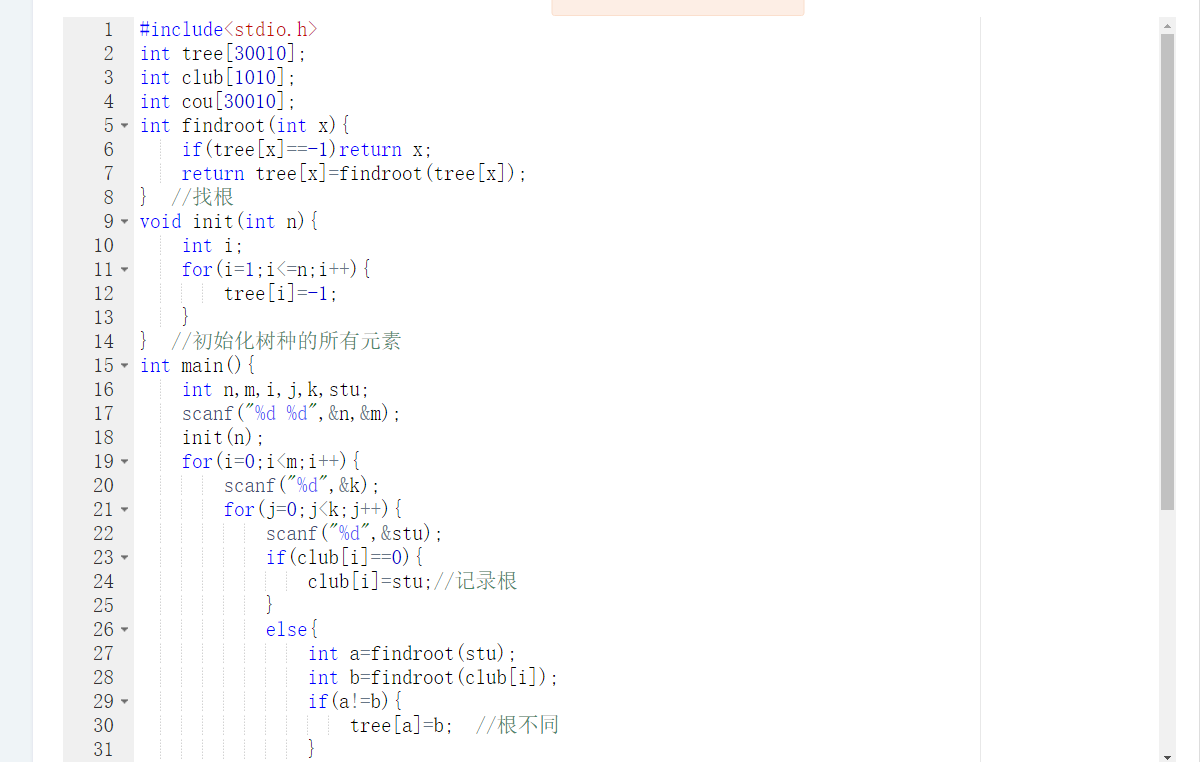

3.PTA提交列表说明

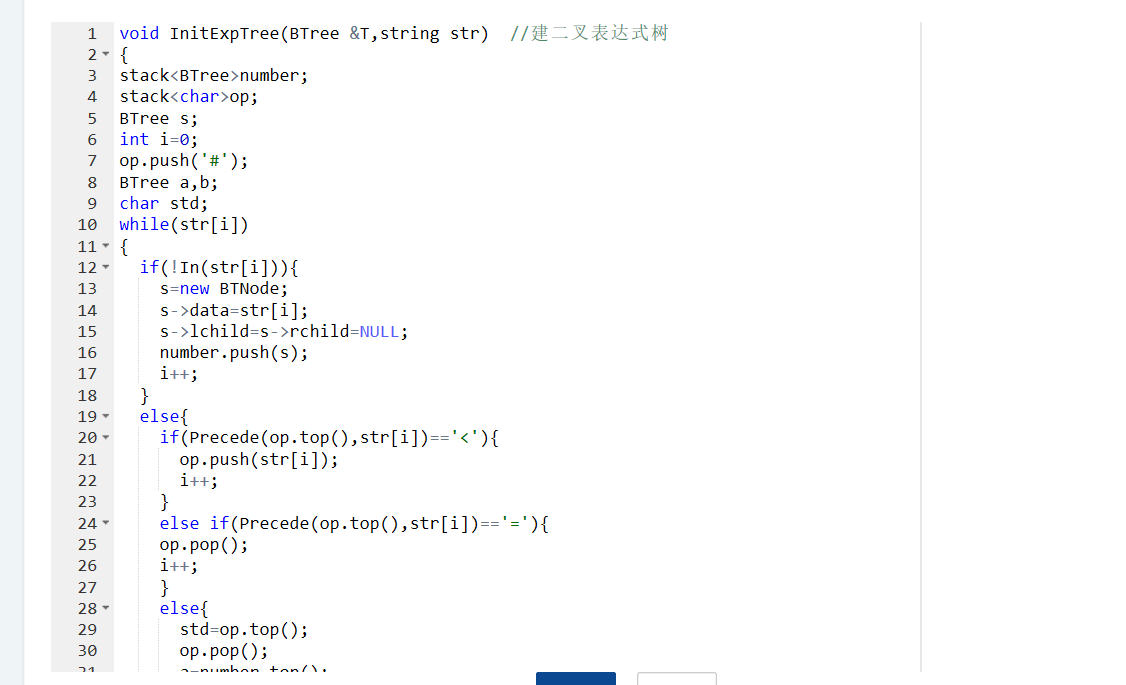
2.1 题目3:表达式树
1 设计思路(伪代码或流程图)
//观察表达式树会发现数字字符的左孩子右孩子都是空的用于后面的表达式树的运算
//创建两个栈一个是树节点的保存类型一个是字符保存栈
for(int i=0;str[i];i++){
if(字符是数字)创建树节点并且入栈
else
{
if(字符栈栈顶优先级小于str[i]){
则进栈字符栈
}
else if(字符栈栈顶优先级大于str[i]){
出栈并且从节点栈中拿出两个;
构树并且放回节点栈中
}
else{
直接出栈
}
}
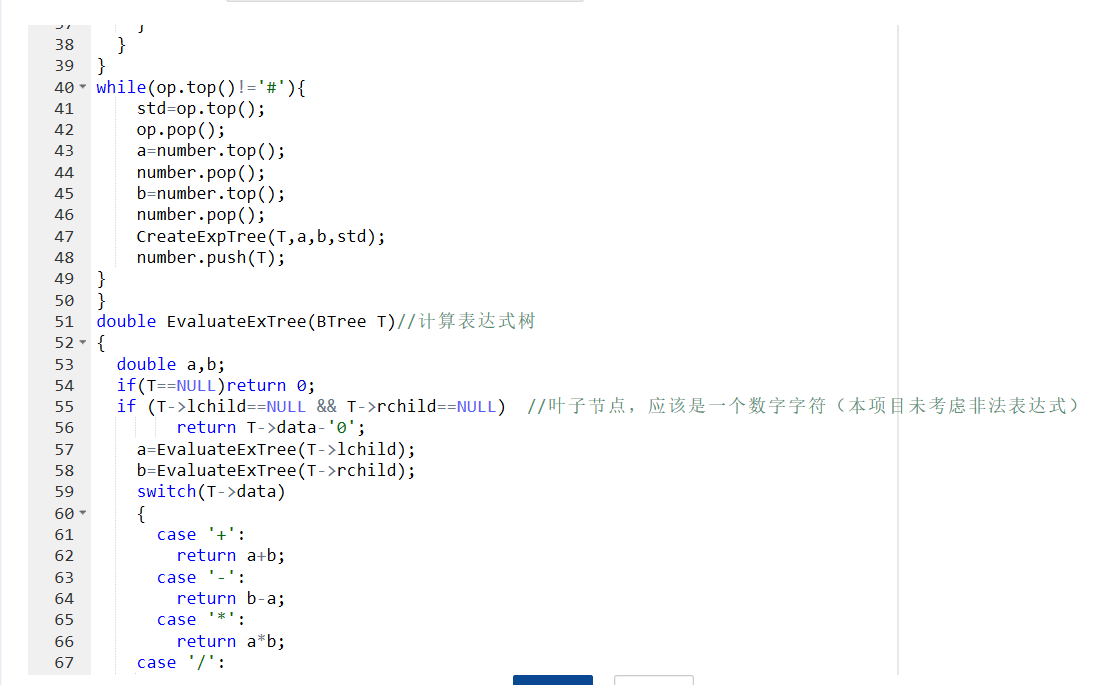
计算表达式
{
if(BT->rchild==NULL&&BT->lchild==NULL)
return BT->data-'0'
else{
a=计算遍历右树
b=计算遍历左树
switch()
{
case '+':return a+b;
case '-':return a-b
case '*':returna*b
case '/':return a/b
}
}
2.代码截图
3.PTA提交列表说明

3.3 我的总分:230

四. 阅读代码(必做,1分)
5-27 家谱处理 (30分)
#include <stdio.h>
#include<stdlib.h>
#include<string.h>
/* 评测结果 时间 结果 得分 题目 编译器 用时(ms) 内存(MB) 用户
2016-08-30 10:31 全部正确 25 5-27 gcc 1 1 569985011
测试点结果 测试点 结果 得分/满分 用时(ms) 内存(MB)
测试点1 答案正确 18/18 1 1
测试点2 答案正确 2/2 1 1
测试点3 答案正确 5/5 1 1
测试点4 答案正确 5/5 1 1
查看代码*/
typedef struct node *Node;
struct node {
char Name[11];
int space;
int Parant;
};
Node Tree;
int n;
int Scan(char*);
int Trace(int);
int judgeParent(int,int);//父子
int judgeSibling(int,int);//兄弟
int judgeAncestor(int,int);//祖先
void work();
int Index(char*);
int main() {
int m;
scanf("%d%d",&n,&m);
Tree=(Node)malloc(sizeof(struct node)*n);
getchar();//清除缓存
for(int i=0; i<n; i++) {
Tree[i].space=Scan(Tree[i].Name);
Tree[i].Parant=i;
}
Tree[0].Parant=-1;
for(int i=0; i<m; i++) {
work();
getchar();
}
return 0;
}
int judgeParent(int x,int y) {
if(Tree[x].Parant==x)Tree[x].Parant=Trace(x);
return Tree[x].Parant==y;
}
int judgeSibling(int x,int y) {
if(Tree[x].Parant==x)Tree[x].Parant=Trace(x);
if(Tree[y].Parant==y)Tree[y].Parant=Trace(y);
return Tree[x].Parant==Tree[y].Parant;
}
int judgeAncestor(int x,int y) {
while(x!=-1) {
if(judgeParent(x,y))return 1;
else x=Tree[x].Parant;
}
return 0;
}
void work() {
char StrX[11],StrY[11],relation[11];
scanf("%s%*s%*s%s%*s%s",StrX,relation,StrY);
// printf("%s - %s - %s\n",StrX,relation,StrY);
int X=Index(StrX);
int Y=Index(StrY);
// printf("%d - %d",X,Y);
int result;
switch(relation[0]) {
case 'c':
result=judgeParent(X,Y);
break;
case 'p':
result=judgeParent(Y,X);
break;
case 's':
result=judgeSibling(X,Y);
break;
case 'd':
result=judgeAncestor(X,Y);
break;
case 'a':
result=judgeAncestor(Y,X);
break;
default:
result=-1;
break;
}
if(result==1)printf("True\n");
else if(!result)printf("False\n");
// else printf("ERROR:系统不能识别所指定关系!\n");
}
int Index(char*a) {
for(int i=0; i<n; i++) {
// printf("*");
if(strcmp(Tree[i].Name,a)==0)return i;
}
// printf("ERROR:所给人名不存在!\n");
return -1;
}
int Trace(int child) { //往前遍历第一个比他缩进少的就是他的父亲
for(int i=child-1; i>=0; i--) {
if(Tree[i].space<Tree[child].space) {
// printf("%d's parent is %d'",child,i);
return i;
}
}
return -1;//如果没有,那么他就是亚当夏娃了。
}
int Scan(char*p) {
char c;
int space=0;
while((c=getchar())==' ')space++;//记录字符串前面的空格数量
do {
*p++=c;
} while((c=getchar())!='\n');
*p='\0';
return space;
}
这一题我一开始的想法就是先建立一个树家谱关系树,确实建立成功勒,但是后面的各个关系的处理判断我就不会了.

这个输入方式就可以忽略没用的信息
然后就是从数组去寻找这两个名字的位置后转换为各个小问题的处理,
这种处理方式真的很容易非常巧妙还有就是它有保留家谱中每个人的信息是用数组处理的
五. 代码Git提交记录截图