【机器学习算法基础+实战系列】SVM
概述
支持向量机是一种二分类模型,间隔最大使它有别于感知机。支持向量机学习方法由简至繁的模型:线性可分支持向量机(linear support vector machine in linearly separable data),线性支持向量机(linear support vector machine),非线性支持向量机(non-linear support vector machine). 简单模型是复杂模型的基础,也是复杂模型的特殊情况。当训练数据线性可分的时候,通过硬间隔最大化(hard margin maximization)学习一个线性分类器,也就是线性可分支持向量机。当训练数据近似线性可分的时候,我们通过软间隔最大化(soft margin maximization)学习一个线性分类器,即线性支持向量机。当数据线性不可分时,通过核技巧和软间隔最大化,学习非线性支持向量机。
线性可分支持向量机和硬间隔最大化
首先对于我们的数据集合假定为是线性可分的,也就是说存在那么一条直线(或者超平面)可以将我们的数据集按照类别的不同分开。如下图所示
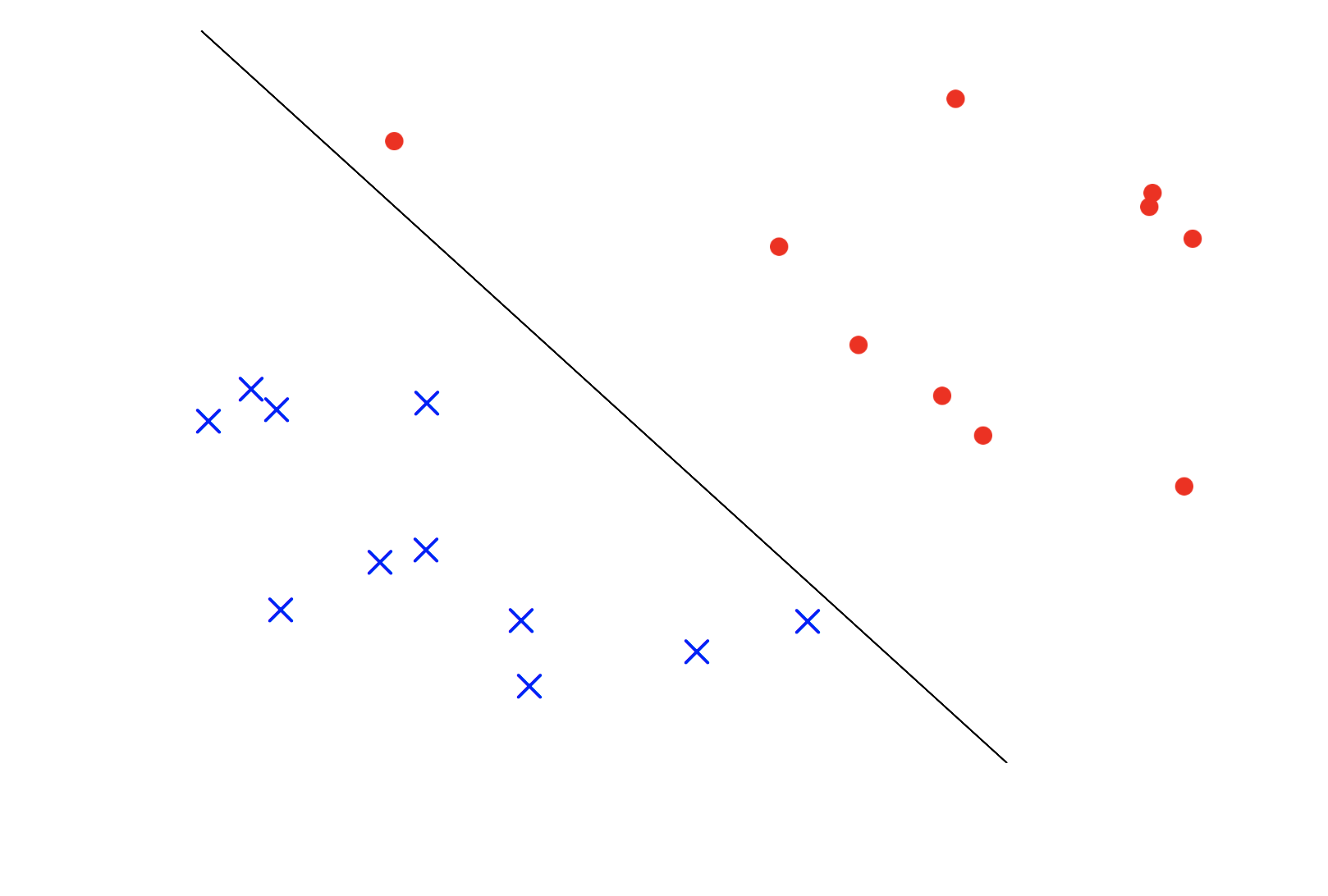
从上图我们可以知道这条黑色的线(在多维空间是一个超平面)可以将不同类别的点分开来。
但是我们知道,一般情况下,当数据线性可分的条件下,这样的超平面很大程度上不是只存在一个,而是很多个, 我们使用什么标准来从中选择一个最优的超平面呢?那就是分类平面到两侧的距离越远代表着分类的效果越好。简单解释一下原因是距离越远代表着我们的容错率越高。比如我们的训练集合中的数据和测试集合中的数据特性有着些许差别,超平面到点的距离越近,代表着这个差别对分类效果的影响越大,所以只有尽可能的扩大这个距离,才能让我们的分类超平面的效果在测试集合上越好。
这就引出来了SVM,换句话来讲,SVM的学习策略就是使得间隔最大化,同时将求解超平面的问题转化为一个凸二次规划问题的求解。
线性可分支持向量机: 给定线性可分数据集,通过间隔最大化求解二次凸规划问题得到的超平面为:\(w^{T}x+b=0\) 以及相应的分类决策函数为: \(f(x)= sign(w^{T}x+b)\). 我们称之为线性可分支持向量机.
几何间隔:
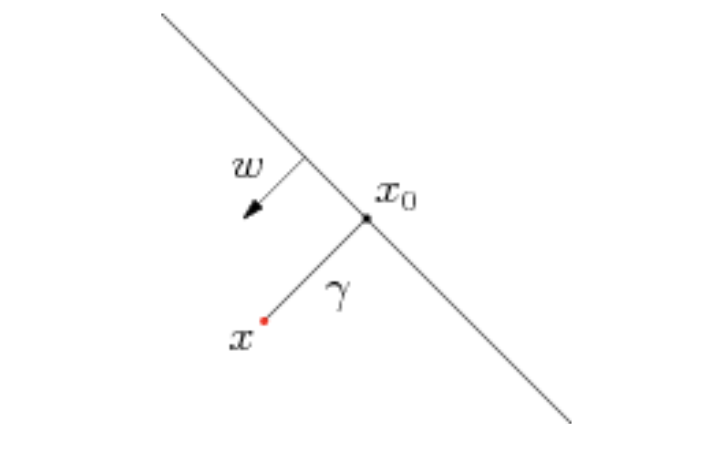
假设对于一个点\(x\),令其垂直投影到超平面上的对应点为\(x_{0}\), \(w\)是垂直于超平面的一个法向量, \(\gamma\). 根据平面几何知识,有$$ x=x_{0}+\gamma \frac{w}{||w||}$$.因为\(x_{0}\)是超平面上的一点,所以满足\(w^{T}x_{0}+b=0\). 然后让 \(x=x_{0}+\gamma \frac{w}{||w||}\)的两边同时乘上\(w^{T}\).根据\(w^{T}x_{0}=-b和w^{T}w=||w||^{2}\),可以得到:\(\gamma=\frac{w^{T}x+b}{||w||}\).随后我们为了得到绝对值,从而得到几何间隔: \(\frac{|w^{T}x+b|}{||w||}\)
SVM的二次规划求解超平面问题(原始模式)
对于训练数据集来讲:$$D={x_{n},y_{n}}^{N}{n=1},x\in R^{d},y_{n}\in{-1,+1}$$
正如上面所讲的,我们需要找到一个最优平面,我们使用距离的最大化来确定最优平面的\(w和b\).
我们知道从\(x_{n}\)这个点到到超平面的距离是:$$d=\frac{|w^{T}x_{n}+b|}{||w||}$$.
超平面两侧点到面的距离和为:$$\min\limits_{x_{n},y_{n}=-1} d+\min\limits_{x_{n},y_{n}=+1} d$$
现在我们得到目标函数:$$max \frac{1}{||w||} \space\ s.t., y_{i}(w^{T}x_{i}+b)\geq1,i=1,2...,n$$
我们将求\(\frac{1}{||w||}\)的最大值问题转化为求\(\frac{||w||^{2}}{2}\)的最小值的问题,即$$min \frac{||w||^{2}}{2} \space\ s.t., y_{i}(w^{T}x_{i}+b)\geq1,i=1,2...,n$$.
所以现在问题就转化成了一个凸优化的问题(目标函数是二次函数,约束条件是线性的),对于这种问题我们可以使用任何一种凸优化的运算工具得到结果。
上一种情况是在线性可分的情况下进行的SVM,如果是非线性可分的情况,我们需要做的就是讲\(x\)映射到高维空间,即\(z_{n}=\phi(x_{n})\),然后将\(\phi(n)\)带入到二次规划求解的问题中就可以。
SVM对偶模式求解最优超平面
除了用解决QP问题的常规方法之外,我们还可以通过求解对偶问题得到最优解,这就是线性可分条件下的支持向量机的对偶运算。这种运算的优先在于:一更加的简洁,二自然的引入核函数,推广到非线性分类的问题。
在这个过程中,我们使用的是Lagrange duality 变换到对偶变量的优化问题,通过给每一个约束条件加上一个Lagrange Multiplier,也就是引入拉格朗日乘子\(\alpha\)
随后我们将min和max对换位置:
交换位置之后的新问题是原始问题的对偶问题,这个问题的最优值用\(d^{*}\)来表示,他表示原始问题最优值\(p^{*}\)的下限。在满足强对偶条件下,两者去取等号。所以这时候的问题就变成了先对w,b求极小值,在对\(\alpha\)求极大值。
对偶问题的3个步骤:
(1)首先固定\(\alpha\), 分别对w,b 求偏导数
\(\frac{\partial \mathcal{L}}{\partial w} =0 \Rightarrow w= \sum_{i=1}^{n}\alpha_{i}y_{i}x_{i}\)
\(\frac{\partial \mathcal{L}}{\partial b} =0 \Rightarrow \sum_{i=1}^{n}\alpha_{i}y_{i }=0\)
将这两个结果带回到$ \mathcal{L}(w,b,\alpha)\(得到如下结果:
\)-\frac{1}{2}\sum_{i=1}{n}\sum_{j=1}\alpha_{i}\alpha_{j}y_{i}y_{j}x_{i}{T}x_{j}+\sum_{i=1}\alpha_{i}$
(2)得到上面的式子之后,我们发现拉格朗日函数中只含有一个变量,那就是\(\alpha_{i}\),接下来我们就可以去求最优问题:
这也是一个二次规划问题,我们使用程序可以得到结果
线性支持向量机与软间隔最大化
数据近似线性可分,说明有一部分数据不线性可分,为了解决这个问题,我们对于每个点都引入一个松弛变量\(\xi_[i]\geq 0\),从而约束条件变成了\(y_{i}(w^{T}x_{i}+b\geq 1-\xi_{i}\). 目标函数也就\(frac{1}{2}||w||^{2}\)变为了\(frac{1}{2}||w||^{2}+C\sum_{i=1}^{N}\xi_{i}\). 在这里我们把\(C>0\)称为惩罚参数,一般由应用问题决定。当C值大时,对误分类点的惩罚增大,当C值小时,对误分类点的惩罚减小. 这时候就可以进行同上的操作,最后得到函数:$$\max\limits_{\alpha} \space\ -\frac{1}{2}\sum_{i=1}{n}\sum_{j=1}\alpha_{i}\alpha_{j}y_{i}y_{j}x_{i}{T}x_{j}+\sum_{i=1}\alpha_{i}$$ $$s.t. \sum_{i=1}^{n}y_{i}\alpha_{i}=0 \space\ 0\leq\alpha_{i} \leq C i=1,2,...,n $$
核函数Kernel
我们知道对于线性条件下SVM具有原始模式和对偶模式,都可以求出最优解,我们为什么还要提出来对偶模式呢?这就是为了解决在原始空间非线性的情况。
一般来说,对于非线性情况,我们的常用做法是把样例特征映射到高维空间中去(如上文2.2节最开始的那幅图所示,映射到高维空间后,相关特征便被分开了,也就达到了分类的目的);
但是如果高维空间维度太大,这个时候我们就需要将核函数用在对偶SVM上,简化运算。
对核函数的具体讲解可以参考这里核函数
对SVM的三重理解




