博客作业06--图
1.学习总结
1.1图的思维导图
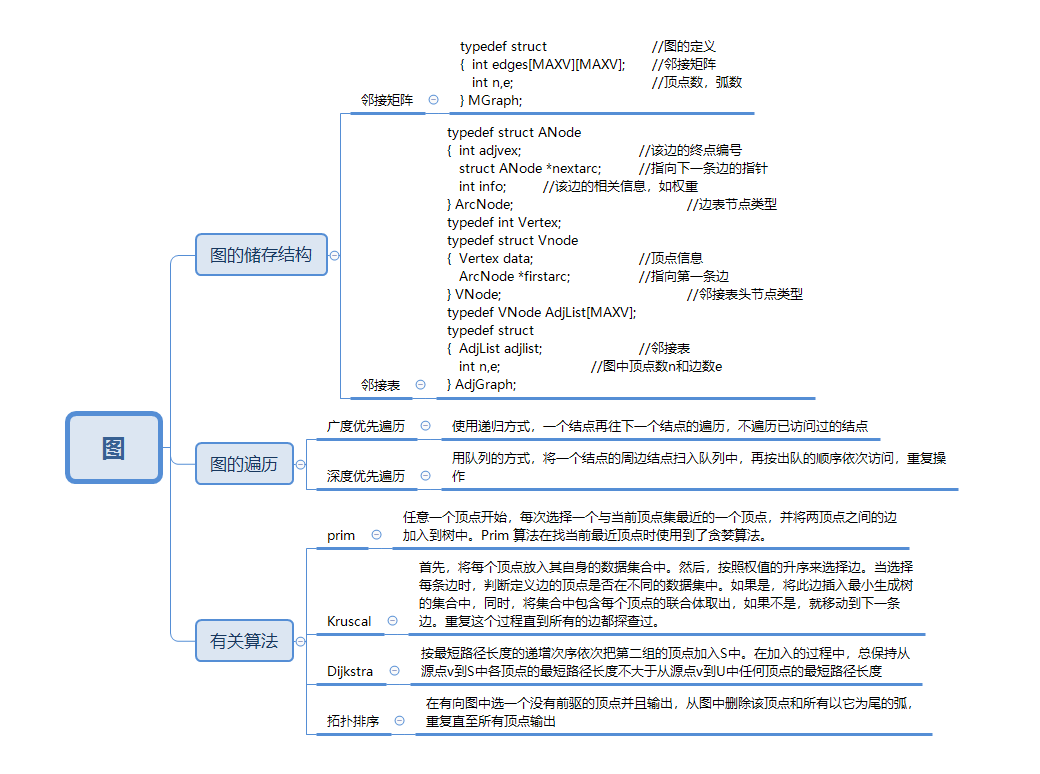
1.2 图结构学习体会
深度遍历算法:图的深度优先遍历类似于树的前序遍历。采用的搜索方法的特点是尽可能先对纵深方向进行搜索。
可以解决很多相关的图论问题,如最大路径问题等等
广度遍历算法:它的思想是从一个顶点V0开始,辐射状地优先遍历其周围较广的区域。可以解决广度优先生成树,
最短路径等问题
Prim和Kruscal算法:解决最小生成树的问题,最短路径等问题
Dijkstra算法:解一个图的一个点(称之为原点)到其余各点(称之为周边点)的最短路径问题
拓扑排序算法:是由某个集合上的一个偏序得到该集合上的一个全序。
2.PTA实验作业
2.1 题目1:7-1 图着色问题
2.2 设计思路
创建图
把数据录入
a数组用来储存颜色
for i=0 to i=m-1
把数组初始化
for j=1 to j=n
把着色方法存入数组
判断 如果颜色的种类与num不相同或check(g)==0
输出No
如果check(g)==1
输出yes
check函数:
如果相连的两点它们的颜色一样(a[i]==a[j])
就return 0
循环结束没有提前return 说明方法可行
return 1
2.3 代码截图
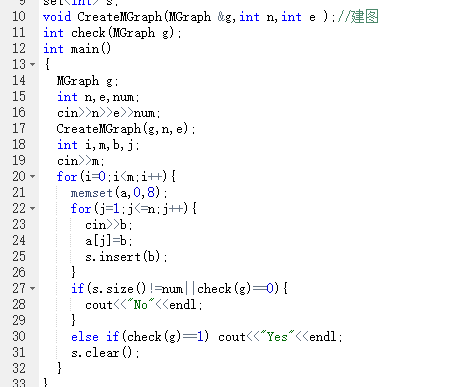

2.4 PTA提交列表说明。

本题没有碰到什么大的问题。
2.1 题目2:7-2 排座位
2.2 设计思路
Judefriend函数:
for i=1 to i=n
判断两人之间是否还有相同的朋友
有return 1
没有 return 0
主函数
数组初始化
二维数组数据填充
for i=1 to i=k
输入要判断的两人
如果他们关系为1
输出No problem
如果关系为0
输出ok
如果关系为 -1 且经过判断他们有相同朋友
输出 ok but
else
输出no way
2.3 代码截图
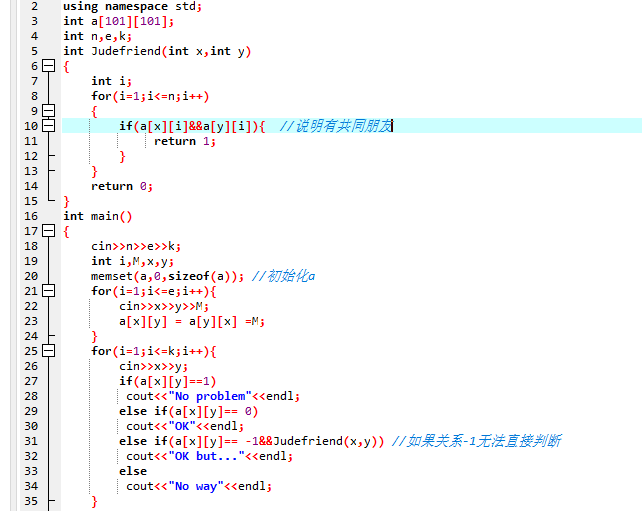
2.4 PTA提交列表说明。

部分正确:一开始做是用图的方法,感觉思路正确一直过不去,后来就用二维数组思路相同就通过了。
2.1 题目3:7-4 公路村村通
2.2 设计思路
主函数
把二维数组每个值都初始化为无限大
把数据输入数组
从点1开始判断这些路的最短路的和
Prim函数
sum初始化为0
{lowcost数组储存连接该点周围路的长度
for i=1 to i=n
把lowcost初始化为点1周围的路径
访问过就置lowcost为-1
找出这些路径中最短的那条
如果k值改变
{ 把最短的那条路径长加入sum
把要访问的点变为该路连接的另一点}
更新lowcost的值}
判断村是否全部相连
是返回sum的值
不是返回 -1
2.3 代码截图


2.4 PTA提交列表说明。
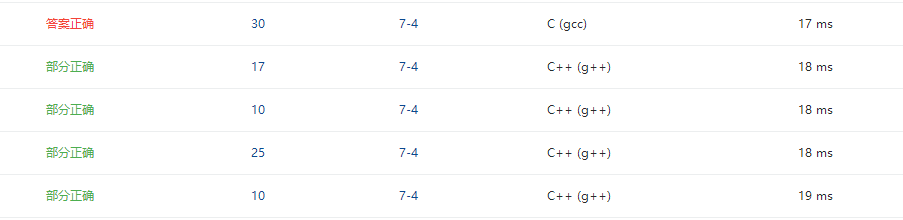
部分正确:一直有个点没有过去,后来经过不断尝试发现时判断村是否全部连通的问题,在询问同学后成功解决。
3.截图本周题目集的PTA最后排名
3.1 PTA排名

3.2 我的总分:225
4. 阅读代码
从前,在一个王国中,在 nn 个城市间有 mm 条道路连接,而且任意两个城市之间至多有一条道路直接相连。
在经过一次严重的战争之后,有 dd 条道路被破坏了。国王想要修复国家的道路系统,现在有两个重要城市
AA 和 BB 之间的交通中断,国王希望尽快的恢复两个城市之间的连接。你的任务就是修复一些道路使
AA 与 BB 之间的连接恢复,并要求修复的道路长度最小。
#include<cstdio>
#include<queue>
#include<iostream>
using namespace std;
const int maxn=500002,inf=2147483647;
//边至少要开2倍:因为是无向边,连接两相同节点的边要加两次,所以理论最大边数为n(n-1)≈n^2,因此理论最大被毁坏边数为n^2,此处多开了一些,并无影响;
struct Edge{
int to,next,v;
}e[maxn];//建立边表;
int head[maxn],dis[maxn],a[maxn],b[maxn];
bool vis[maxn];
queue<int>q;
int n,m,d,s,t,cnt;
void add(int u,int v,int w)//链式前向星存图;
{
e[++cnt].to=v;
e[cnt].next=head[u];
e[cnt].v=w;
head[u]=cnt;
}
void spfa()//采取spfa求AB之间的最短路,当然也可以用dijkstra等;
{
for(int i=1;i<=n;i++)
dis[i]=inf,vis[i]=0;
dis[s]=0;
vis[s]=1;
q.push(s);
while(!q.empty())
{
int u=q.front();
q.pop();
vis[u]=0;
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].to;
if(dis[v]>dis[u]+e[i].v)
{
dis[v]=dis[u]+e[i].v;
if(!vis[v])
{
vis[v]=1;
q.push(v);
}
}
}
}
}
int main()
{
int x,y,z,ans;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);
add(y,x,z);
//无向边。
}
scanf("%d",&d);
for(int i=1;i<=d;i++)
scanf("%d%d",&a[i],&b[i]);//由于需要起点和终点,所以要保存起来,输入起点终点后再使用;
scanf("%d%d",&s,&t);
spfa();
ans=dis[t];//ans为假定畅通时的长度;
for(int i=1;i<=d;i++)
{
add(a[i],b[i],0);
add(b[i],a[i],0);
//可以直接加边的原因是,根据spfa的原理,两点之间即使有多条边,最终都将被更新为最短的那一条;
}
spfa();
ans-=dis[t];//此时的ans就是答案了;
printf("%d",ans);
return 0;
}
跑一遍A到B的最短路,然后将被毁坏的道路边权设为0,再跑一遍最短路。两次所得的B的最短路之差,
就是最短路径上需要修复的路的长度。路径上某些边的权变成0后,再得的最短路只会变得更短或者不变
该题类型看似与pta几题公路的相似但又有所不同,思路大体还是找最短路径。






