博客作业03--栈和队列

1.学习总结

概念理解

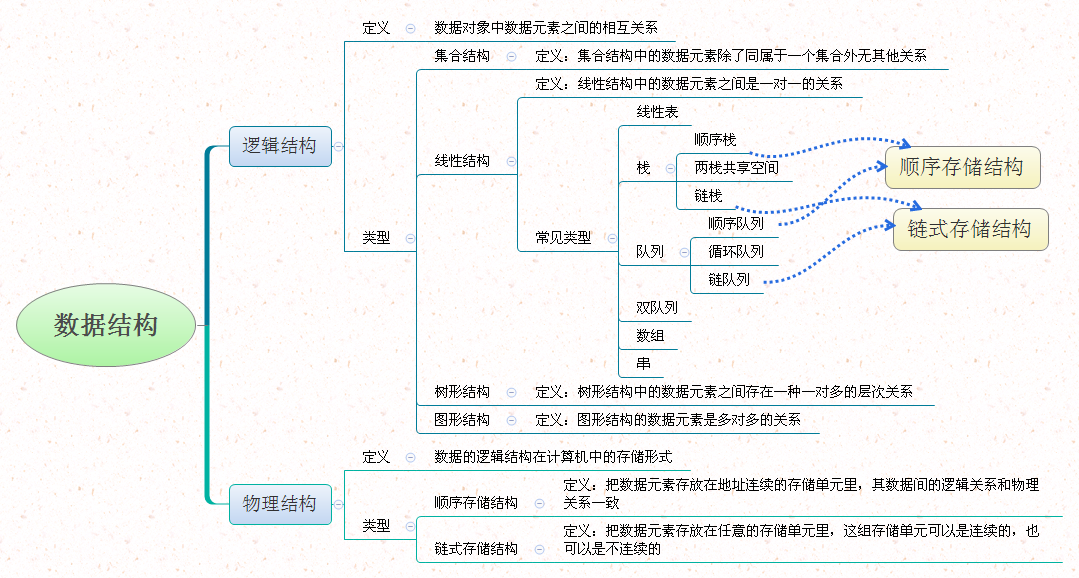
逻辑结构

• 逻辑结构就是数据之间的关系。而按数据之间的关系来说，逻辑结构大概可以分为两种：线性结构和非线性结构（集合、树、网）。
• 线性结构：有且只有一个开始结点和一个终端结点，并且所有结点都最多只有一个直接前驱和一个直接后继。例如：线性表，典型的线性表有：顺序表、链表、栈（顺序栈、链栈）和队列（顺序队列、链队列）。它们共同的特点就是数据之间的线性关系，除了头结点和尾结点之外，每个结点都有唯一的前驱和唯一的后继，也就是所谓的一对一的关系。
• 非线性结构：对应于线性结构，非线性结构也就是每个结点可以有不止一个直接前驱和直接后继。常见的非线性结构包括：树（二叉树）、图（网）等。

存储结构

• 逻辑结构指的是数据间的关系，而存储结构是逻辑结构的存储映像。通俗的讲，可以将存储结构理解为逻辑结构用计算机语言的实现。常见的存储结构有顺序存储、链式存储、索引存储以及散列存储（哈希表）。
• 顺序存储：把逻辑上相邻的节点存储在物理位置上相邻的存储单元中，结点之间的逻辑关系由存储单元的邻接关系来体现。由此得到的存储结构为顺序存储结构，通常顺序存储结构是借助于数组来描述的。优点：节省空间，可以实现随机存取；缺点：插入、删除时需要移动元素，效率低。
• 链式存储：在计算机中用一组任意的存储单元存储线性表的数据元素(这组存储单元可以是连续的,也可以是不连续的)。特点是元素在物理上可以不相邻，所以每个数据元素包括了一个数据域和一个指针域，数据域用来存放数据，而指针域用来指向其后继结点的位置。优点：插入、删除灵活；缺点：不能随机存取，查找速度慢。

逻辑结构和存储结构的区别

• 这两者并不冲突，一个指的是数据之间的关系，而另一个指这种关系在计算机中的表现形式。比如，线性表中的栈，数据元素之间的关系是一对一的，除头和尾结点之外的每个结点都有唯一的前驱和唯一的后继，这体现的是逻辑结构；而对于栈中的结点来说，它们可以顺序存储（也就是顺序栈），取一段连续的存储空间，将栈结点按顺序存入，每个结点和其前驱和后继在物理上都是相邻的。同时，栈结点也可以链式存储（链栈），每个结点中包括数据域和指针域，而指针域就是用来指向其后继的，在访问时就可以通过指针来找到其后继进行访问，每个结点之间物理上可以相邻也可以不相邻。

栈（stack）

• 栈是限定仅在表尾进行插入和删除操作的线性表

队列（queue）

• 队列是只允许在一端进行插入操作，而在另一端进行删除操作的线性表

栈和队列的异同点

• 栈和队列均可以用线性表的顺序存储结构来实现，但都存在着顺序存储的一些弊端。因此它们各自有各自的技巧来解决这个问题。
• 对于栈来说，如果是两个相同数据类型的栈，则可以用数组的两端作栈底的方法来让两个栈共享数据，这就可以最大化地利用数组的空间。
• 对于队列来说，为了避免数组插入和删除时需要移动数据，于是就引入了循环队列，使得队头和队尾可以在数组中循环变化。解决了移动数据的时间损耗，使得本来插入和删除是O（n）的时间复杂度变成了O（1）
• 它们也都可以通过链式存储结构来实现，实现原则上与线性表基本相同

2.PTA实验作业

2.1 题目1：7-3 表达式转换

2.2 设计思路

while(从exp读取字符ch,ch!='\0’)
{	ch为左括号'(' : 判断后一个字符e是否为字符'+''-',若是，说明'+''-'是正负号，则继续读取这个数字并以空格结束存放到postexp；若不是，则将此括号进栈到S中；
	ch为右括号')' : 将S中出栈时遇到的第一个左括号'('以前的运算符都依次出栈并每次以空格结束存放到postexp中
	ch为'+'或'-' : 判断ch是否在exp的开头，若是，说明'+''-'为正负号，则直接存放在postexp中；若不是，则出栈运算符依次出栈并每次以空格结束存放到postexp中，直到栈空或者栈顶为'('，然后将ch进栈；
	ch为'*'或'/' : 出栈运算符依次出栈并每次以空格结束存放到postexp中，直到栈空或者栈顶为'('、'+'或'-',然后ch入栈
	ch为数字或小数点：将后续的所有数字均依次存放到postexp中，并以空格标识数字串结束；
}
    若exp扫描完毕，则将S中的所有运算符依次出栈并存放到postexp中且每次以空格标识存放结束;

2.3 代码截图

2.4 PTA提交列表及说明

• Q1：多种错误

• A1：一开始没有注意到格式问题，然后再加上没有考虑到正负号等等导致的答案错误就形成了一开始的多种错误

• Q2：部分正确：运算符前有正负号——答案错误

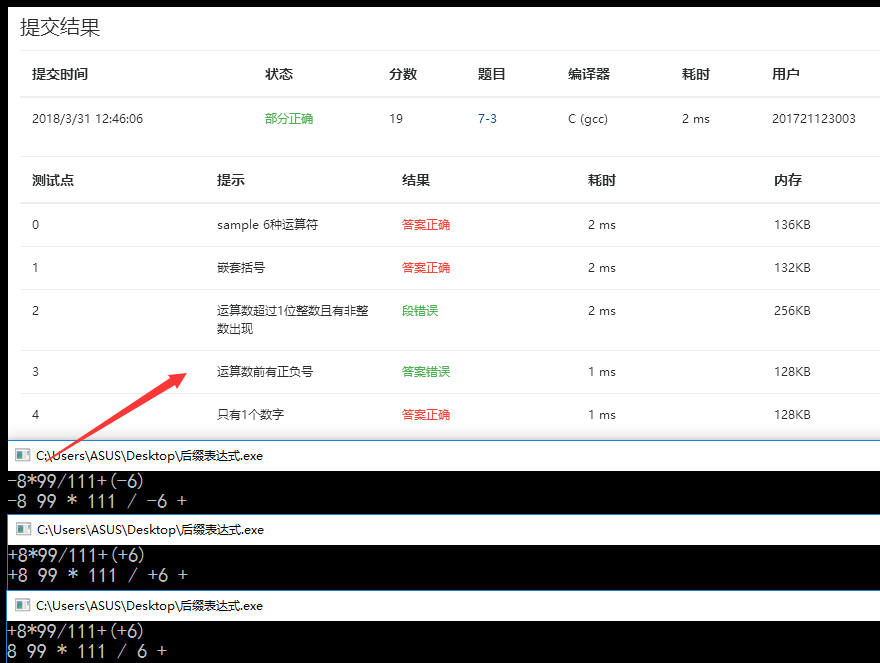
• A2：由分析可知，如果 + - 出现在表达式开头或者是出现在（的右边的话，就说明+ - 为正负号，于是在原代码的基础上增加对这两种情况的判断，若是这两种情况的话，就直接把+ -放到postexp，即把它同数字一般处理。在DevC上用负数进行测试发现输出正确结果于是乐呵呵去提交但是运算符前面有正负号的测试点还是过不了，于是自己进行正号的测试输出后知道应该是如果是正号的话不用表达出来，经过一点点修改后就通过这个测试点啦

• Q3：运算数超过1位整数且有非负整数出现——段错误

• A3：其实就是小数问题，这个问题看上去挺复杂的样子但是思考一下就知道其实就是ch为数字的情况多加一个小数点的情况，同数字一样处理就好啦~

2.1 题目2：7-2 符号配对

2.2 设计思路

定义变量pre，cur分别存放前一个字符和当前字符
while（某一行中不是只有一个句点.和一个回车）
{
	if(栈顶元素是'*'）：判断前一个字符和当前字符是否分别为'*'和'/'，若是，则把栈顶两元素'/'和'*'弹出，若不是，则继续读字符而并不需要进入else分支进行匹配判断
	else（栈顶元素不是'*'）：
		if（当前字符为'('或 '['或'{'）进栈
		if（前一个字符为'/'且当前为'*'）则把这两个都进栈，并且跳过后面的判断进行下一次的读取字符
		if（当前字符为')'或']'或'}'） 则判断栈顶元素是否为对应匹配的符号（ '(''[''{' ），若是，则说明匹配成功，出栈左括号；若不是，判断栈顶是否有元素，有的话说明是左符号匹配失败；无的话是右符号匹配失败，输出对应内容并直接跳出循环
	pre = cur；
}
if（前面的匹配过程并没有出现错误）：判断栈里是否还有元素，若无，说明匹配成功；若有，则说明左括号匹配失败，输出对应内容

2.3 代码截图

2.4 PTA提交列表说明。

• Q1：一开始并不知道匹配失败的话输出规则是什么
• A1：输出第一个匹配错误的地方，比如(]输出(匹配失败，至于左符号多余就输出第一个左符号匹配失败，右符号多余就输出第一个右符号匹配失败
• Q2：对
  这个比较特殊的符号一开始的想法是想把这两个换成p，然后入栈，把
  用q来替代
• A2：但是后来发现没有必要反而加大代码量，于是引入了pre和cur两个变量来便于讨论
  的问题
• Q3：一直部分正确了非常非常久，从提交列表就可以看出我深深的绝望
• A3：这么让人绝望有意义的难题当然是只能问大神啦，然后他给我的建议是，要符合c语言里的规则，就是/……/里的都算是注释内容，并不需要进行符号匹配判断啥的，还有这种操作一语点醒梦中，然后对代码中的while加入第一个if的判断以后终于答案正确了

2.1 题目3：7-3 银行排队问题之单队列多窗口服务

2.2 设计思路

1.定义变量min_ser，min_wait表示等待时间最少的窗口和所需要的等待时间，定义顾客结构体数组a来存放客人信息（到达时间T,处理事务时间P，等待时间wait），定义服务窗口结构体数组b来存放窗口信息（招待客人数量count和工作时间worktime）
2.输入客人的信息，并初始化客人的等待时间为0，初始化服务窗口信息为0
3.for（从第一个客人遍历到最后一个客人）
{
	min_wait=0;
	min_ser =0;
	令flag=0来表示该客人还没有安排好
	for（从第一个窗口遍历到最后一个窗口）
	{
	  if（客人的到达时间大于某窗口的工作时间，说明客人在该窗口不用等）客人wait=0，窗口count++，窗口工作时间=该客人到达时间+处理事务时间，令flag=1来表示客人已经安排好了，并跳出循环
}
	else（客人来的时候窗口在忙）客人wait=窗口worktime-客人T，并与前面遍历的窗口的等待时间最小值进行比较，若小于最小等待时间，就更新最小等待时间，并记录下对应窗口号
}
4.遍历结束后，若还没安排好，则说明所有的窗口都需要等待，那么选取最小等待时间的窗口
5.最后把所有客人的等待时间相加后输出，然后遍历窗口数组找到最大的worktime就是最后的finishtime，并按顺序输出各个窗口接待顾客数量count

2.3 代码截图

2.4 PTA提交列表说明。

• Q1：其实运行输出结果完全不对

• A1：老崩溃了，硬着头皮回去看了一遍代码以后很快就发现原来是找到空闲窗口以后应该直接break出来了就不用后面的比较不然后面的空窗口也会一直的count也会迷之增加的
  

• Q2：加了个break答案就对多啦~但是完成时间又有点不太对，

但是觉得自己代码写得有理有据的就试着去提交顺便看看有哪些测试点

• A2：发现就一个测试点没有过~

正好是完成时间，超过60分钟...emmm...然后又返回回去看题目，才明白原来题目那句顾客事务被处理的最长时间为60分钟就是强行把超过60分钟的顾客P改成60，这个操作放在输入顾客信息的时候就可以搞定啦~然后就输出正确结果然后就全部正确啦

• Q3：不要问我为什么全部正确了还有Q3，因为前面两个都有三个问题的喂!还有!我发现这题是出在队列里面喂!可是我并没有用到关于队列的思想...心情复杂...
• A3：无解...流下不会念书的泪水...

3.截图本周题目集的PTA最后排名

3.1 栈PTA排名

3.2 队列PTA排名

3.3 我的总分：

248

阅读代码

#include<stdio.h>
#include<iostream>
#include<string.h>
#include<algorithm>
#include<math.h>
#include<vector>
using namespace std;
struct node
{
    int u;
    int v;
}a[10005];
int vis[10005];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=m;i++)
       cin>>a[i].u>>a[i].v;
    int k;
    cin>>k;
    while(k--)
    {
        int len,flag=0,b;
        cin>>len;
        memset(vis,0,sizeof(vis));    //将num中的成员全都初始化为0
        for(int i=1;i<=len;i++)
        {
            cin>>b;
            vis[b]=1;
        }
        for(int i=1;i<=m;i++)
        {    //判去除删掉的点剩下的城市是否孤立无援
            if(vis[a[i].u]||vis[a[i].v])
                continue;
            else
                flag=1;
        }
        if(!flag)
            printf("YES\n");
        else
            printf("NO\n");
    }
    return 0;
}

• 该代码功能是：给n个城市，m条路，之后给出k种方案，每种方案给出q个城市，判断解放这q个城市之后，能不能使所有城市全部独立（每一个城市和其他城市都不相连）
• 该代码优点是：巧妙地利用两个数组把问题复杂的问题转化成简单的问题，其思路是：假设这m条路中有3-4这条路，那么这个方案里要么得解放一个3，要么得解放一个4，否则3-4就是一条连通路，输出NO。用这个理论判断所有的路，也就是说每一条路的两个端点城市都要在方案中找到至少一个
• 代码相关地址：https://blog.csdn.net/moonlighttlj/article/details/79777246

5. 代码Git提交记录截图