完全背包问题

完全背包问题

有N 种物品和一个容量为V 的背包，每种物品都有无限件可用。放入第i 种物品的费用是Ci，价值是Wi。求解：将哪些物品装入背包，可使这些物品的耗费的费用总和不超过背包容量，且价值总和最大。

现在的问题在于每个物品都有无限种，因此不能像01背包那样决定i物品放或者不放，因为放的话有多种可能，0件，1件，2件......

现在回顾01背包里的一维dp:

 

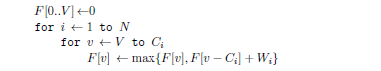
 之所以01背包能缩小到一维dp，是因为我们考虑i的放与不放时，dp[j]与dp[j-Ci]都必须是在i-1的状态下，也就是说是i-1个物品放入j容量背包和i-1个物品放入j-Ci个物品的最大值问题。如果采用逆序，当进行到j时，由于j-Ci<j，因此还没更新，dp[j-Ci]还表示的是i-1时刻的状态。而如果采用正序的方式，当进行到j时，dp[j-Ci]已经更新了，表示的已经是i时刻的状态了，因此不能采用正序。

而在完全背包中，当我们考虑i物品时，如果不放1件，也就是说只有0~i-1这几种物品往j容量背包里放，这个状态下的最大值是dp[j],是i-1时刻的状态。而如果放，由于要考虑放1件，2件还是3件。。。。，因此不能使用i-1时刻的状态了，因为i-1时刻的状态中只有0~i-1共i种物品，而我们现在已经确定要放了，因此必须要是i时刻下的背包，也就是说dp[j-Ci]此时必须处于i时刻，而不能是i-1时刻。

因此，完全背包实际上只要调整内循环的次序就可以解决了：

 

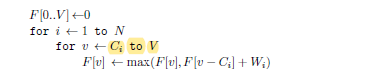
 这样，当进行到(i,v)时，由于还未更新，F[v]表示容量v的背包里放0~i-1种物品的最大价值，也就是不放第i种物品。而当我决定i物品一定要放进去时，此时占去一个位置，则只要知道F[v-Ci]的最大值就好了，而F[v-Ci]必须表示i时刻下的背包最大价值，因为在递增到v之前，i物品也是要可以放入背包的。