20162320大二第8周学习总结
学号20162320 《程序设计与数据结构》第8周学习总结
教材学习内容总结
一、二叉查找树
二叉查找树,对于每个结点n,n的左子树中包含的元素都小于n中的元素,n的右子树中包含的元素都大于等于n中的元素,即左子树上的元素小于父结点的值,而右子树上的元素大于等于父结点的值。如下图所示。根结点的左子树每个元素都小于80,右子树每个元素都大于80.

查找方法,要判定一个具体的目标是否存在于树中,需要沿着从根开始的路径,根据查找目标是小于还是大于当前结点的值,相应地转到当前结点的左子结点或右结点。最终或是找到目标元素,或是遇到路径的末端,后者意味着目标不在树中。
在二叉查找树中添加元素,改过程类似于树的查找过程,新元素添加为树的叶结点,从根开始,沿着每个结点中元素所确定的路径,直到相应地方向上没有子结点为止,此时,将新元素添加为叶结点。
如果没有其他操作,二叉查找树的树形由元素的添加顺序来决定。
注:如果输入是完全有序的,二叉查找树就会退化为一个有序链表,削弱了它本身的价值,如下图所示。
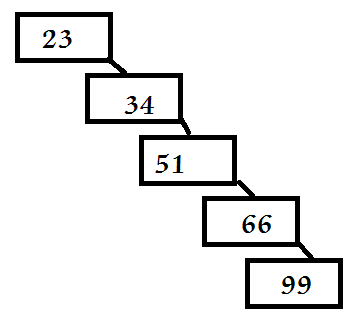
在二叉查找树中删除元素,要考虑如下三种情况(参考下图):
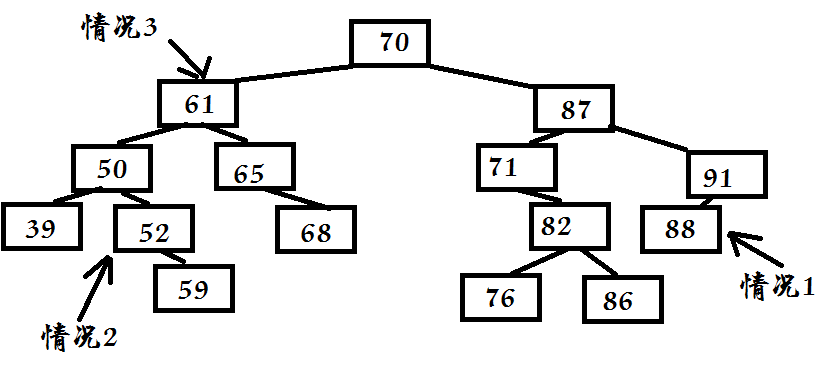
- 第一种情况:如果被删除的结点是叶结点(无子结点),可以简单地删除
- 第二种情况:如果被删除的结点是只有一个子结点,则用它的子结点替代它
- 第三种情况,如果被删除结点有两个子结点,在树的更低层找到一个合适的结点来代替它。被删除结点的子结点成为替代结点的子结点。
当从二叉查找树中删除有两个子结点的结点是,比较好的办法是用它的中序后继来取代它,即在中序遍历中排在被删元素之后的那个元素(紧邻的下一个值)
二、平衡二叉查找树
在平衡二叉树中进行查找,比在退化的树中进行查找的效率高很多。在有n个结点的平衡树中进行查找及添加操作的效率是进行O(log2 n)次比较(最长路径的长度)。树越退化,查找及添加操作的时间复杂度越接近O(n),它抵消了使用查找树带来的益处。
可以对二叉查找树进行旋转以恢复平衡
右旋转
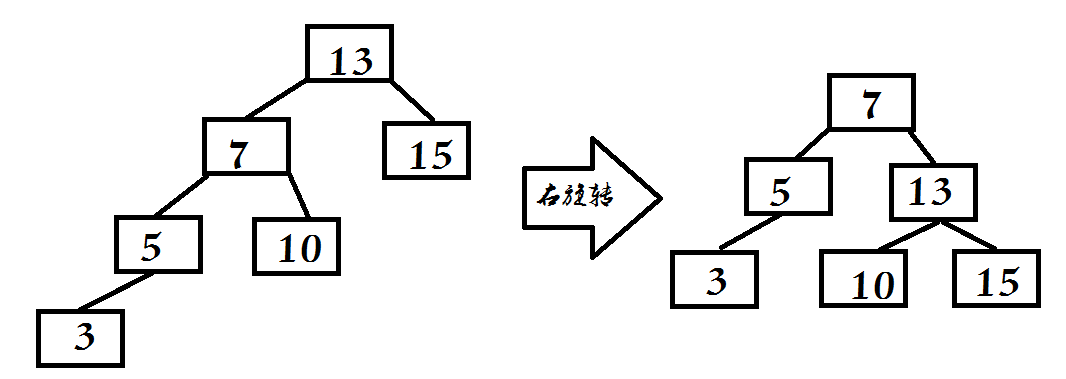
- 1.令根的左子结点变为新的根
- 2.令原根结点变为新的根结点的右子结点
- 3.令原根的左子结点的右子结点变为原根结点的新的左子结点
右旋转
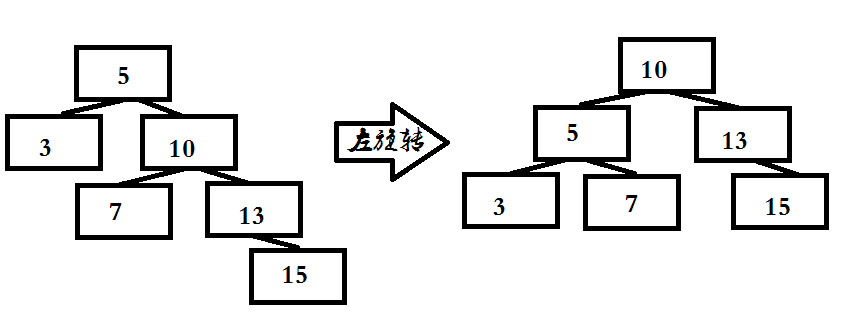
- 1.令根的右子结点变为新的根
- 2.令原根结点变为新的根结点的左子结点
- 3.令原根的右子结点的左子结点变为原根结点的新的右子结点
并非所有的不平衡情况都可以用一个单一的旋转解决,如果不平衡性是由根的右子结点的左子树的长路径引发的,则必须先绕那个异常子树执行一次右旋转,然后再绕根执行一次左旋转(右-左旋转)。如果不平衡是由根的左子结点的右子树中的长路径引发,则执行(左-右旋转)
教材学习中的问题和解决过程
- 问题1:二叉查找树与二分查找算法有什么区别呢?
解答:二叉查找树和第13章的二分查找算法有相同的目的;组织并处理数据,这样每次比较可以排除大约一半的数据。二分查找算法对有序数组进行操作,而二叉查找树用它的结构来组织数据。 - 问题2:当从二叉查找树中删除元素,最困难的情形是什么?
解答:当从二叉查找树中删除一个元素时,最困难的情形是元素有两个子结点时,因为没有简单的选项用来替代元素(如它只有一个子结点或没有子结点) - 问题3:为什么二叉查找树的平衡性(或接近平衡)如此重要?
解答:如果二叉查找树是平衡的,每次比较都会排除差不多一半的元素。树越不平衡,它力线性结构越近,效率也就越低。
代码学习中的问题及解决
详情见我的实验博客
代码托管
(statistics.sh脚本的运行结果截图)
上周考试错题总结
暂未给出答案
结对及互评
点评过的同学博客和代码
- 本周结对学习情况
其他(感悟、思考等,可选)
我会像奥德休斯一样, 朝着心中的方向 ,哪怕众神会在彼岸阻挡 。当我需要独自站在 ,远方的沙场 ,武器就是我紧握的梦想 ,而我受过的伤 ,都是我的勋章 。继续加油!
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 188 | 1/1 | 25 | 算法分析 |
| 第二周 | 70/258 | 1/2 | 15/40 | 《构建之法》7-9章 |
| 第三周 | 474/732 | 1/3 | 20/60 | 查找和排序 |
| 第四五六周 | 1313/2045 | 4/7 | 12/72 | 栈和队列 |
| 第七周 | 890/2935 | 1/8 | 14/86 | 树 |
| 第八周 | 913/3848 | 1/9 | 20/106 | 二叉查找树 |
| 第九周 |
- 计划学习时间: 20+小时
- 实际学习时间: 25小时
(有空多看看现代软件工程 课件 软件工程师能力自我评价表)



