20162320刘先润大二第7周学习总结
学号20162320 《程序设计与数据结构》第7周学习总结
教材学习内容总结
一.树
树是非线性结构,其中的元素组织为一个结构层次。而之前的集合(栈、队列及链表)都是线性数据结构,即他们的元素可以一个接一个排列。
树(tree)是有一组边(edge)够构成,结点用来保存元素,边表示结点之间的连接。
如下图所示,书中较低一层的结点称为其前一层结点的子节点(children),一个结点只能有一个父结点,但一个结点可以有多个子结点,有相同结点的结点称为兄弟结点(sibling)。 根结点是树中唯一没有父结点的结点。没有任何子结点的结点称为叶结点(leaf)。至少一个子结点的非根结点称为内部结点(internal node)。 树中构成另一棵树结构的部分称为子树(subtree)从根的路径上,位于上面的顶点是其下方顶点的祖先(ancestor),根是树中所有结点的最终祖先,从一个结点沿路径可以到达的结点称为它的后继(decendant)。结点的层是从根到该结点的路径长度(path length)。
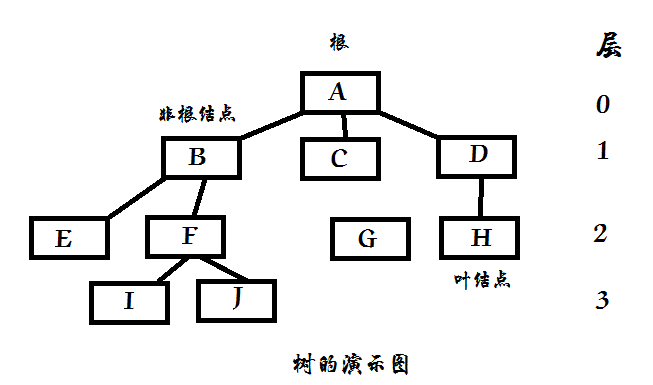
树可以按很多方式分类,其中一种方法是按树中任意结点的最大子结点个数来分,这个值有时称为数的度(order)
另一种分类方法是看树是否平衡,如果树的所有子结点都在同一层上,或彼此最多不超出一层,则认为树是平衡的。
有m个元素的平衡n叉树的高度是lognm。
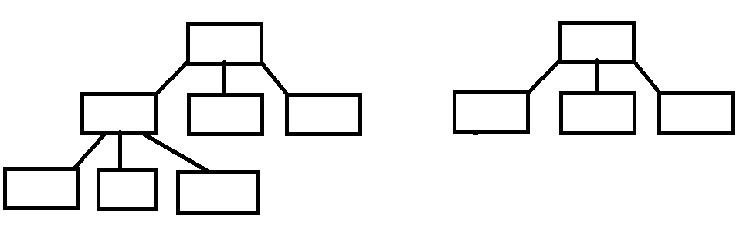
每个结点最多有两个子结点的树称为二叉树。如果树的所有叶结点都在同一层,并且每个非叶结点都正好有n个子结点,则称n叉树是满的(full);如果树是满的,或一直到倒数第二层都是满的且最底层的所有叶结点都位于树的左侧,则称树是完全的(complete)。如下图左边的树是完全树,但不是满的,右边的树即是完全的,也是满的。
二. 树的遍历
进行层序遍历时可用队列来存储树中的元素
树的遍历有4中方法:
- 1.先序遍历(preordor traversal)——访问根,自作左至右遍历子树
- 2.中序遍历(inorder traversal)——遍历左子树,然后访问根,然后自左至右遍历余下的各个子树
- 3.后序遍历(postorder traversal)——自左至右遍历各子树,然后访问根
- 4.层序遍历(level-order travelsal)——从树的顶层(根)到底层,从左至右,访问树中每层的每个结点
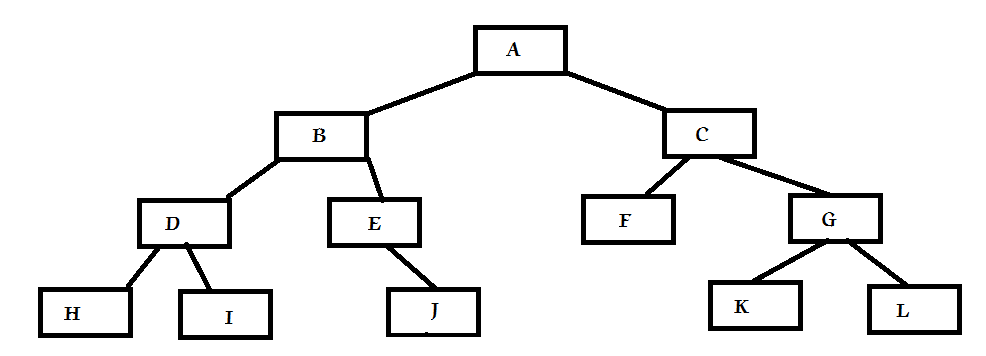
如上图,不同遍历方法的访问顺序也不同。先序遍历:A→B→D→H→I→E→J→C→F→G→K→L; 中序遍历:H→D→I→B→E→J→A→F→C→K→G→L;后序遍历:H→I→D→J→E→B→F→K→L→G→C→A ;层序遍历:A→B→C→D→E→F→G→H→I→J→K→L
三.树的实现策略
- 1.在数组中计算链
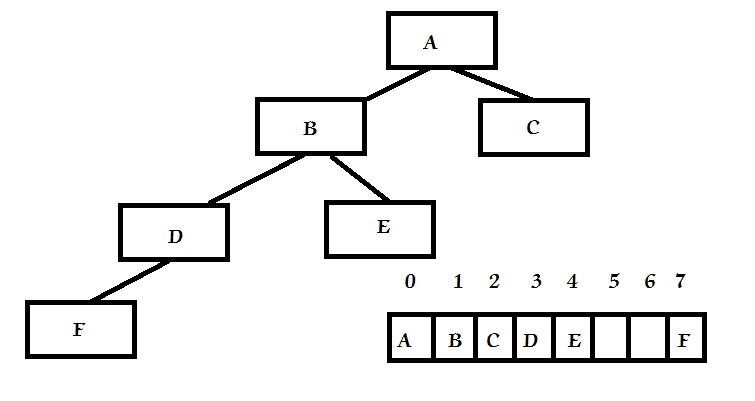
对于满树或完全二叉树来说,可以使用一个数组来表示树。策略是:对于存储在数组中位置为n的元素,元素的左结点存储在(2n+1)的位置,元素的右结点存储在(2×(n+1))的位置。如下图
- 2.在数组中保存链
数的基于数组的存储链实现方式可以占据数组中的连续位置,不管树是不是完全树
模仿操作系统内存管理的方法,不是根据元素在树中的位置来指定它在数组中的存储位置,而是采用先来先服务的策略将它们分配在数组的一片连续位置中。数组的每个元素是一个对象,它保存指向树中元素的引用及每个子结点所在的数组下标。在下图中,假定进入树的次序假定是A、C、B、E、D、F。A左下标为2,即B在数组中的位置,右下标为1,即C在数组中的位置。如果一个结点没有子结点,那么它对应的下标为-1。
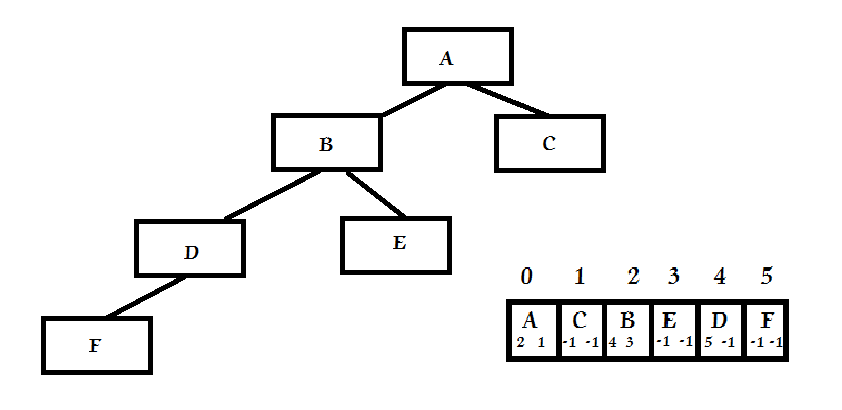
当需要将树结构直接存储到硬盘中时,也可以采用这一策略。这种情况下,数组下标不再作为指针使用,每个结点保存的是它的子结点在文件中的相对位置,这样给定文件的头地址后,就可以计算偏移量。
四.二叉树与决策树
如何在一般二叉树中添加及删除元素,要取决于树的用途。
使用决策树可以设计专家系统
决策树(dcision tree)的结点表示判定点,结点的孩子表示那一刻可用的选择,决策树的叶结点表示根据选择得到的结论。
专家系统(expert system)是表示特定领域专家知识的一种软件系统
我写的一个简单的决策树如下图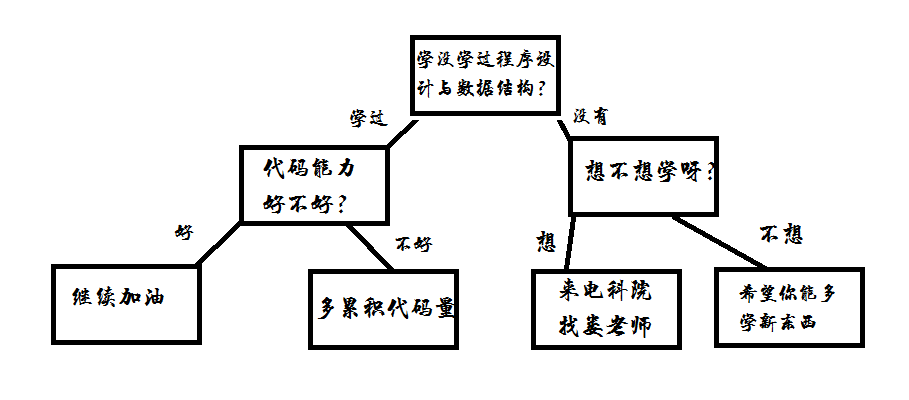
五.性质
二叉树的性质,若二叉树的根节点位于第1层:
- 1.在二叉树的第i层最多有
2的n-1次方个结点(i≥1) - 2.深度为k的二叉树最多有
2的k-1次方个结点(k≥1) - 3.对任意一棵二叉树,如果其叶结点个数为n0,度为2的结点树为n2,则有n0=n2+1
完全二叉树的性质,
- 性质1.具有·n个结点的完全二叉树的高度是
(log2 n)+1 - 性质2.如果将一棵有n个结点的完全二叉树自顶向下,同一层自左向右连续给结点编号1,2,…n,则对于任意结点i(1≤i≤n),有:1.若i=1,则该i结点是树根,它无双亲;2.若2i>n,则编号为i的结点无左孩子,否则他的左孩子是编号为
2*i的结点;3.若2i+1>n,则编号为i的结点无右孩子,否则其右孩子结点编号为2*i+1
教材学习中的问题和解决过程
- 问题1:树的先序遍历和后序遍历有什么区别呢?
解答:树遍历将访问树中的每个元素。遍历类型决定了何时访问结点。先序遍历在访问根的两个子树之前先访问它,而后序遍历则在访问它的两个子树之后再访问根。 - 问题2:满树必须是完全树吗?
解答:解决这个问题必须完全掌握二者的定义。1,:满二叉树:除最后一层无任何子节点外,每一层上的所有结点都有两个子结点(最后一层上的无子结点的结点为叶子结点)。除叶子结点外的所有结点均有两个子结点。节点数达到最大值。所有叶子结点必须在同一层上。:2:完全二叉树:若一棵二叉树至多只有最下面的两层上的结点的度数可以小于2,并且最下层上的结点都集中在该层最左边的若干位置上,则此二叉树成为完全二叉树。
所以说,满二叉树是完全二叉树的特例,因为满二叉树已经满了,而完全并不代表满。 - 问题3:用计算链实现二叉树的优势和不足有哪些?
解答:计算链策略不需要保存父结点和子结点之间的链,因为关系由数组中的位置来决定。但是这个策略对不平衡树及/或不完全树,可能会浪费树的存储空间。
代码托管
(statistics.sh脚本的运行结果截图)
上周考试错题总结
- 1.A queue is the ideal collection to use when ____________________ .
解答:模拟实现一行, 队列是在模拟中实现一条线路的理想选择,例如先到先得的情况。 - 2.In a array-based implementation of a queue that stores the front of the queue at index 0 in the array, the dequeue operation is ___________________.
解答:O(n),在删除应用程序之后,需要将队列的所有元素移到索引上,这需要一个线性的时间量。
3.It is possible to implement a stack and a queue in such a way that all operations take a constant amount of time.
解答:这句话是正确的,因为堆栈和队列的理想实现具有所有需要一定时间的操作。
结对及互评
点评过的同学博客和代码
- 本周结对学习情况
其他(感悟、思考等,可选)
不停地奔赴,寻找最初的梦想,理清层层苦忧,锁定展望方向,才能解开迷团浇开迷雾,终有一个满意的归宿。有句话说的好“”流水千觞,光阴有限,趁着阳光初早,明媚如鲜,我们还处于人生的最好时期,真情面对各自的美好前程,踏实履行坚定的脚印,才会不枉此生,绽放璀璨的光辉“希望我的代码能力能够对得起我不懈的努力,最后恭祝十九大胜利召开。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 188 | 1/1 | 25 | 算法分析 |
| 第二周 | 70/258 | 1/2 | 15/40 | 《构建之法》7-9章 |
| 第三周 | 474/732 | 1/3 | 20/60 | 查找和排序 |
| 第四五六周 | 1313/2045 | 4/7 | 12/72 | 栈和队列 |
| 第七周 | 2203/2935 | 1/8 | 14/86 | 树 |
| 第八周 |
- 计划学习时间: 12+小时
- 实际学习时间: 25小时
(有空多看看现代软件工程 课件 软件工程师能力自我评价表)



