pta 编程题10 Root of AVL Tree

其它pta数据结构编程题请参见：pta

这道题考察平衡二叉查找树的插入。

为了保证二叉查找树的平衡，当一个结点的左右子树的高度差大于1时就要进行调整。

分为以下四种情况：

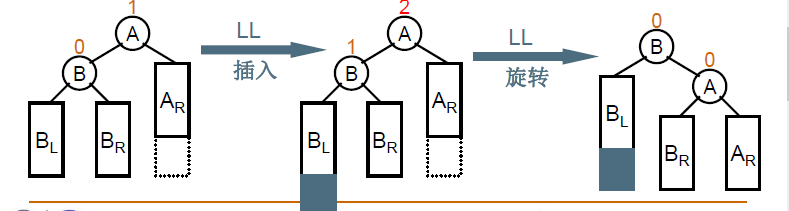
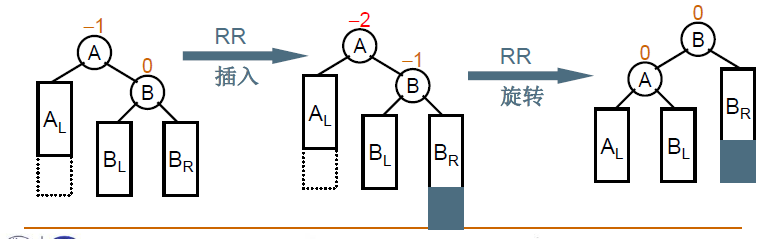
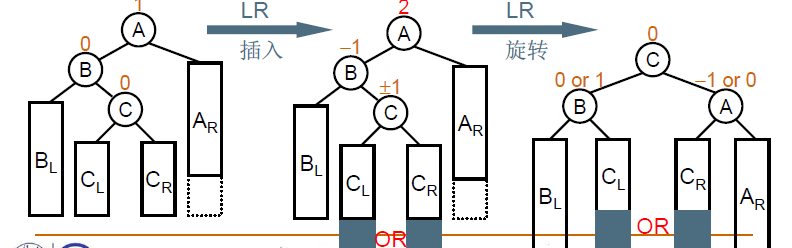
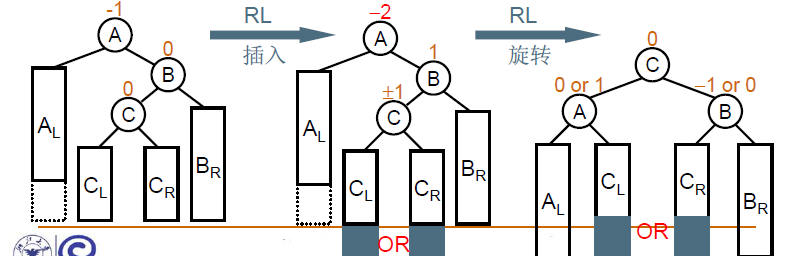
插入新节点后，以及旋转之后，需要更新结点的高度。

RL旋转可以通过右孩子的LL旋转，然后当前节点的RR旋转实现。

同理，LR旋转可以通过左孩子的RR旋转，然后当前节点的LL旋转实现。

  1 #include <iostream>
  2 using namespace std;
  3 
  4 typedef struct Node *Tree;
  5 struct Node
  6 {
  7     int data;
  8     Tree left;
  9     Tree right;
 10     int height;
 11 };
 12 
 13 Tree insert(Tree T, int X);
 14 Tree ll(Tree A);
 15 Tree lr(Tree A);
 16 Tree rr(Tree A);
 17 Tree rl(Tree A);
 18 int getHeight(Tree T);
 19 int max(int a, int b);
 20 Tree createNode(int X);
 21 
 22 int main()
 23 {
 24     int N, X, i;
 25     cin >> N >> X;
 26     Tree root = createNode(X);
 27     for (i = 1; i < N; i++)
 28     {
 29         cin >> X;
 30         root = insert(root, X);
 31     }
 32     cout << root->data;
 33     return 0;
 34 }
 35 
 36 Tree insert(Tree T, int X)
 37 {
 38     if (!T)
 39         T = createNode(X);
 40     else if (X < T->data)
 41     {
 42         T->left = insert(T->left, X);
 43         if (getHeight(T->left) - getHeight(T->right) == 2)
 44         {
 45             if (X < T->left->data)
 46                 T = ll(T);
 47             else
 48                 T = lr(T);
 49         }
 50     }
 51     else if (X > T->data)
 52     {
 53         T->right = insert(T->right, X);
 54         if (getHeight(T->right) - getHeight(T->left) == 2)
 55         {
 56             if (X > T->right->data)
 57                 T = rr(T);
 58             else
 59                 T = rl(T);
 60         }
 61     }
 62     T->height = max(getHeight(T->left), getHeight(T->right)) + 1;
 63     return T;
 64 }
 65 
 66 Tree ll(Tree A)
 67 {
 68     Tree B = A->left;
 69     A->left = B->right;
 70     B->right = A;
 71     A->height = max(getHeight(A->left), getHeight(A->right)) + 1;
 72     B->height = max(getHeight(A->left), A->height) + 1;
 73     return B;
 74 }
 75 
 76 Tree rr(Tree A)
 77 {
 78     Tree B = A->right;
 79     A->right = B->left;
 80     B->left = A;
 81     A->height = max(getHeight(A->left), getHeight(A->right)) + 1;
 82     B->height = max(A->height, getHeight(B->right)) + 1;
 83     return B;
 84 }
 85 
 86 Tree lr(Tree A)
 87 {
 88     A->left = rr(A->left);
 89     return ll(A);
 90 }
 91 
 92 Tree rl(Tree A)
 93 {
 94     A->right = ll(A->right);
 95     return rr(A);
 96 }
 97 
 98 int getHeight(Tree T)
 99 {
100     if (T == NULL) return 0;
101     else return T->height;
102 }
103 
104 int max(int a, int b)
105 {
106     return a > b ? a : b;
107 }
108 
109 Tree createNode(int X)
110 {
111     Tree T;
112     T = new Node;
113     T->data = X;
114     T->left = T->right = NULL;
115     T->height = 1;
116     return T;
117 }
View Code

 

posted @ 2018-04-12 22:34  bloglxc  阅读(175)  评论(0)  编辑  收藏  举报