ORB-SLAM（三）地图初始化

单目SLAM地图初始化的目标是构建初始的三维点云。由于不能仅仅从单帧得到深度信息，因此需要从图像序列中选取两帧以上的图像，估计摄像机姿态并重建出初始的三维点云。

ORB-SLAM中提到，地图初始化常见的方法有三种。

方法一

追踪一个已知物体。单帧图像的每一个点都对应于空间的一条射线。通过不同角度不同位置扫描同一个物体，期望能够将三维点的不确定性缩小到可接受的范围。

方法二

基于假设空间存在一个平面物体，选取两帧不同位置的图像，通过计算Homography来估计位姿。这类方法在视差较小或者平面上的点靠近某个主点时效果不好。

参考文献Faugeras et al, Motion and structure from motion in a piecewise planar environment. International Journal of Pattern Recognition and Artificial Intelligence, 1988.

方法三

根据两帧之间的特征点匹配计算Fundamental matrix，进一步估计位姿。这种方法要求存在不共面的特征点。

参考文献Hartley, Richard, and Andrew Zisserman. Multiple view geometry in computer vision. Cambridge university press, 2003.

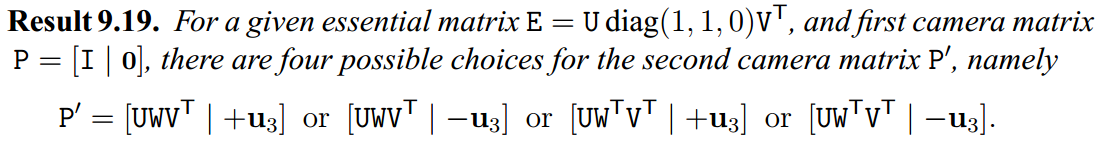
ORB-SLAM的作者提出了一种基于统计的模型选择方法。该方法优先选择第三种方法，并期望在场景退化情形下自动选择第二种方法。如果选取的两帧不满足要求，放弃这两帧并重新初始化。

第一步

提取特征点并匹配，若匹配点足够多，尝试第二步。

第二步

利用匹配的特征点分别计算方法二和方法三。

对每个模型，首先归一化所有的特征点。然后，在每步迭代中，

1. 根据特征点对计算homography或者fundamental matrix。Homography的计算方法为normalized DLT，fundamental matrix的计算方法为normalized 8 points。

2. 计算每个点对的symmetric transfer errors，和卡方分布的对应值比较，由此判定该点是否为内点。累计内点的总得分。

    

   模型选择方法参考4.7.1 RANSAC in Multiple View Geometry in Computer Vision。

    

3. 比较本次得分和历史得分，取最高分并记录相应参数。

第三步

根据一定的准则选择模型。用SH表示homography的得分，SF表示fundamental matrix的得分。如果SH / (SH + SF) > 0.4，那么选择homography，反之选择fundamental matrix。

第四步

根据选择的模型计算位姿。参考方法二和方法三。

第五步

Full bundle adjustment。

由于ORB-SLAM对初始化的要求较高，因此初始化时可以选择一个特征丰富的场景，移动摄像机给它提供足够的视差。另外，由于坐标系会附着在初始化成功的那帧图像的位置，因此每次初始化不能保证在同一个位置。

下面结合源代码进一步说明一下。

/**
* This file is part of ORB-SLAM2.
*
* Copyright (C) 2014-2016 Raúl Mur-Artal <raulmur at unizar dot es> (University of Zaragoza)
* For more information see <https://github.com/raulmur/ORB_SLAM2>
*
* ORB-SLAM2 is free software: you can redistribute it and/or modify
* it under the terms of the GNU General Public License as published by
* the Free Software Foundation, either version 3 of the License, or
* (at your option) any later version.
*
* ORB-SLAM2 is distributed in the hope that it will be useful,
* but WITHOUT ANY WARRANTY; without even the implied warranty of
* MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
* GNU General Public License for more details.
*
* You should have received a copy of the GNU General Public License
* along with ORB-SLAM2. If not, see <http://www.gnu.org/licenses/>.
*/

#include "Initializer.h"

#include "Thirdparty/DBoW2/DUtils/Random.h"

#include "Optimizer.h"
#include "ORBmatcher.h"

#include<thread>

namespace ORB_SLAM2 {

Initializer::Initializer(const Frame &ReferenceFrame, float sigma, int iterations) {
  mK = ReferenceFrame.mK.clone();

  mvKeys1 = ReferenceFrame.mvKeysUn;

  mSigma = sigma;
  mSigma2 = sigma * sigma;
  mMaxIterations = iterations;
}

bool Initializer::Initialize(const Frame &CurrentFrame, const vector<int> &vMatches12, cv::Mat &R21, cv::Mat &t21,
                             vector<cv::Point3f> &vP3D, vector<bool> &vbTriangulated) {
  // Fill structures with current keypoints and matches with reference frame
  // Reference Frame: 1, Current Frame: 2
  // Frame 2 特征点
  mvKeys2 = CurrentFrame.mvKeysUn;

  mvMatches12.clear();
  mvMatches12.reserve(mvKeys2.size());
  mvbMatched1.resize(mvKeys1.size());
  // 组织特征点对
  for (size_t i = 0, iend = vMatches12.size(); i < iend; i++) {
    if (vMatches12[i] >= 0) {
      mvMatches12.push_back(make_pair(i, vMatches12[i]));
      mvbMatched1[i] = true;
    } else
      mvbMatched1[i] = false;
  }

  const int N = mvMatches12.size();

  // Indices for minimum set selection
  vector<size_t> vAllIndices;
  vAllIndices.reserve(N);
  vector<size_t> vAvailableIndices;

  for (int i = 0; i < N; i++) {
    vAllIndices.push_back(i);
  }

  // Generate sets of 8 points for each RANSAC iteration
  // 为每个iteration选取8个随机的index（在FindHomography和FindFundamental被调用）
  mvSets = vector< vector<size_t> >(mMaxIterations, vector<size_t>(8, 0));

  DUtils::Random::SeedRandOnce(0);

  for (int it = 0; it < mMaxIterations; it++) {
    vAvailableIndices = vAllIndices;

    // Select a minimum set
    for (size_t j = 0; j < 8; j++) {
      int randi = DUtils::Random::RandomInt(0, vAvailableIndices.size() - 1);
      int idx = vAvailableIndices[randi];

      mvSets[it][j] = idx;

      vAvailableIndices[randi] = vAvailableIndices.back();
      vAvailableIndices.pop_back();
    }
  }

  // Launch threads to compute in parallel a fundamental matrix and a homography
  // 调起多线程分别用于计算fundamental matrix和homography
  vector<bool> vbMatchesInliersH, vbMatchesInliersF;
  float SH, SF;
  cv::Mat H, F;

  // 计算homograpy并打分
  thread threadH(&Initializer::FindHomography, this, ref(vbMatchesInliersH), ref(SH), ref(H));
  // 计算fundamental matrix并打分
  thread threadF(&Initializer::FindFundamental, this, ref(vbMatchesInliersF), ref(SF), ref(F));

  // Wait until both threads have finished
  threadH.join();
  threadF.join();

  // Compute ratio of scores
  // 计算比例，选取某个模型
  float RH = SH / (SH + SF);

  // Try to reconstruct from homography or fundamental depending on the ratio (0.40-0.45)
  if (RH > 0.40)
    return ReconstructH(vbMatchesInliersH, H, mK, R21, t21, vP3D, vbTriangulated, 1.0, 50);
  else //if(pF_HF>0.6)
    return ReconstructF(vbMatchesInliersF, F, mK, R21, t21, vP3D, vbTriangulated, 1.0, 50);

  return false;
}


void Initializer::FindHomography(vector<bool> &vbMatchesInliers, float &score, cv::Mat &H21) {
  // Number of putative matches
  const int N = mvMatches12.size();

  // Normalize coordinates
  vector<cv::Point2f> vPn1, vPn2;
  cv::Mat T1, T2;
  Normalize(mvKeys1, vPn1, T1);
  Normalize(mvKeys2, vPn2, T2);
  cv::Mat T2inv = T2.inv();

  // Best Results variables
  score = 0.0;
  vbMatchesInliers = vector<bool>(N, false);

  // Iteration variables
  vector<cv::Point2f> vPn1i(8);
  vector<cv::Point2f> vPn2i(8);
  cv::Mat H21i, H12i;
  vector<bool> vbCurrentInliers(N, false);
  float currentScore;

  // Perform all RANSAC iterations and save the solution with highest score
  for (int it = 0; it < mMaxIterations; it++) {
    // Select a minimum set
    for (size_t j = 0; j < 8; j++) {
      int idx = mvSets[it][j];

      vPn1i[j] = vPn1[mvMatches12[idx].first];
      vPn2i[j] = vPn2[mvMatches12[idx].second];
    }

    cv::Mat Hn = ComputeH21(vPn1i, vPn2i);
    H21i = T2inv * Hn * T1;
    H12i = H21i.inv();

    currentScore = CheckHomography(H21i, H12i, vbCurrentInliers, mSigma);

    if (currentScore > score) {
      H21 = H21i.clone();
      vbMatchesInliers = vbCurrentInliers;
      score = currentScore;
    }
  }
}


void Initializer::FindFundamental(vector<bool> &vbMatchesInliers, float &score, cv::Mat &F21) {
  // Number of putative matches
  const int N = vbMatchesInliers.size();

  // Normalize coordinates
  vector<cv::Point2f> vPn1, vPn2;
  cv::Mat T1, T2;
  Normalize(mvKeys1, vPn1, T1);
  Normalize(mvKeys2, vPn2, T2);
  cv::Mat T2t = T2.t();

  // Best Results variables
  score = 0.0;
  vbMatchesInliers = vector<bool>(N, false);

  // Iteration variables
  vector<cv::Point2f> vPn1i(8);
  vector<cv::Point2f> vPn2i(8);
  cv::Mat F21i;
  vector<bool> vbCurrentInliers(N, false);
  float currentScore;

  // Perform all RANSAC iterations and save the solution with highest score
  for (int it = 0; it < mMaxIterations; it++) {
    // Select a minimum set
    for (int j = 0; j < 8; j++) {
      int idx = mvSets[it][j];

      vPn1i[j] = vPn1[mvMatches12[idx].first];
      vPn2i[j] = vPn2[mvMatches12[idx].second];
    }

    cv::Mat Fn = ComputeF21(vPn1i, vPn2i);

    F21i = T2t * Fn * T1;

    currentScore = CheckFundamental(F21i, vbCurrentInliers, mSigma);

    if (currentScore > score) {
      F21 = F21i.clone();
      vbMatchesInliers = vbCurrentInliers;
      score = currentScore;
    }
  }
}

// 从特征点匹配求homography（normalized DLT）
// Algorithm 4.2 in Multiple View Geometry in Computer Vision.
cv::Mat Initializer::ComputeH21(const vector<cv::Point2f> &vP1, const vector<cv::Point2f> &vP2) {
  const int N = vP1.size();

  cv::Mat A(2 * N, 9, CV_32F);

  for (int i = 0; i < N; i++) {
    const float u1 = vP1[i].x;
    const float v1 = vP1[i].y;
    const float u2 = vP2[i].x;
    const float v2 = vP2[i].y;

    A.at<float>(2 * i, 0) = 0.0;
    A.at<float>(2 * i, 1) = 0.0;
    A.at<float>(2 * i, 2) = 0.0;
    A.at<float>(2 * i, 3) = -u1;
    A.at<float>(2 * i, 4) = -v1;
    A.at<float>(2 * i, 5) = -1;
    A.at<float>(2 * i, 6) = v2 * u1;
    A.at<float>(2 * i, 7) = v2 * v1;
    A.at<float>(2 * i, 8) = v2;

    A.at<float>(2 * i + 1, 0) = u1;
    A.at<float>(2 * i + 1, 1) = v1;
    A.at<float>(2 * i + 1, 2) = 1;
    A.at<float>(2 * i + 1, 3) = 0.0;
    A.at<float>(2 * i + 1, 4) = 0.0;
    A.at<float>(2 * i + 1, 5) = 0.0;
    A.at<float>(2 * i + 1, 6) = -u2 * u1;
    A.at<float>(2 * i + 1, 7) = -u2 * v1;
    A.at<float>(2 * i + 1, 8) = -u2;

  }

  cv::Mat u, w, vt;

  cv::SVDecomp(A, w, u, vt, cv::SVD::MODIFY_A | cv::SVD::FULL_UV);

  return vt.row(8).reshape(0, 3);
}
// 从特征点匹配求fundamental matrix（8点法）
// Algorithm 11.1 in Multiple View Geometry in Computer Vision.
cv::Mat Initializer::ComputeF21(const vector<cv::Point2f> &vP1, const vector<cv::Point2f> &vP2) {
  const int N = vP1.size();

  cv::Mat A(N, 9, CV_32F);

  for (int i = 0; i < N; i++) {
    const float u1 = vP1[i].x;
    const float v1 = vP1[i].y;
    const float u2 = vP2[i].x;
    const float v2 = vP2[i].y;

    A.at<float>(i, 0) = u2 * u1;
    A.at<float>(i, 1) = u2 * v1;
    A.at<float>(i, 2) = u2;
    A.at<float>(i, 3) = v2 * u1;
    A.at<float>(i, 4) = v2 * v1;
    A.at<float>(i, 5) = v2;
    A.at<float>(i, 6) = u1;
    A.at<float>(i, 7) = v1;
    A.at<float>(i, 8) = 1;
  }

  cv::Mat u, w, vt;

  cv::SVDecomp(A, w, u, vt, cv::SVD::MODIFY_A | cv::SVD::FULL_UV);

  cv::Mat Fpre = vt.row(8).reshape(0, 3);

  cv::SVDecomp(Fpre, w, u, vt, cv::SVD::MODIFY_A | cv::SVD::FULL_UV);

  w.at<float>(2) = 0;

  return  u * cv::Mat::diag(w) * vt;
}
// 从homography计算symmetric transfer errors
// IV. AUTOMATIC MAP INITIALIZATION （2） in Author's paper
// symmetric transfer errors:
//    4.2.2 Geometric distance in Multiple View Geometry in Computer Vision.
// model selection
//    4.7.1 RANSAC in Multiple View Geometry in Computer Vision
float Initializer::CheckHomography(const cv::Mat &H21, const cv::Mat &H12, vector<bool> &vbMatchesInliers, float sigma) {
  const int N = mvMatches12.size();

  const float h11 = H21.at<float>(0, 0);
  const float h12 = H21.at<float>(0, 1);
  const float h13 = H21.at<float>(0, 2);
  const float h21 = H21.at<float>(1, 0);
  const float h22 = H21.at<float>(1, 1);
  const float h23 = H21.at<float>(1, 2);
  const float h31 = H21.at<float>(2, 0);
  const float h32 = H21.at<float>(2, 1);
  const float h33 = H21.at<float>(2, 2);

  const float h11inv = H12.at<float>(0, 0);
  const float h12inv = H12.at<float>(0, 1);
  const float h13inv = H12.at<float>(0, 2);
  const float h21inv = H12.at<float>(1, 0);
  const float h22inv = H12.at<float>(1, 1);
  const float h23inv = H12.at<float>(1, 2);
  const float h31inv = H12.at<float>(2, 0);
  const float h32inv = H12.at<float>(2, 1);
  const float h33inv = H12.at<float>(2, 2);

  vbMatchesInliers.resize(N);

  float score = 0;
  // 来源于卡方分布
  const float th = 5.991;

  const float invSigmaSquare = 1.0 / (sigma * sigma);

  for (int i = 0; i < N; i++) {
    bool bIn = true;

    const cv::KeyPoint &kp1 = mvKeys1[mvMatches12[i].first];
    const cv::KeyPoint &kp2 = mvKeys2[mvMatches12[i].second];

    const float u1 = kp1.pt.x;
    const float v1 = kp1.pt.y;
    const float u2 = kp2.pt.x;
    const float v2 = kp2.pt.y;

    // Reprojection error in first image
    // x2in1 = H12*x2

    const float w2in1inv = 1.0 / (h31inv * u2 + h32inv * v2 + h33inv);
    const float u2in1 = (h11inv * u2 + h12inv * v2 + h13inv) * w2in1inv;
    const float v2in1 = (h21inv * u2 + h22inv * v2 + h23inv) * w2in1inv;

    const float squareDist1 = (u1 - u2in1) * (u1 - u2in1) + (v1 - v2in1) * (v1 - v2in1);

    const float chiSquare1 = squareDist1 * invSigmaSquare;

    if (chiSquare1 > th)
      bIn = false;
    else
      score += th - chiSquare1;

    // Reprojection error in second image
    // x1in2 = H21*x1

    const float w1in2inv = 1.0 / (h31 * u1 + h32 * v1 + h33);
    const float u1in2 = (h11 * u1 + h12 * v1 + h13) * w1in2inv;
    const float v1in2 = (h21 * u1 + h22 * v1 + h23) * w1in2inv;

    const float squareDist2 = (u2 - u1in2) * (u2 - u1in2) + (v2 - v1in2) * (v2 - v1in2);

    const float chiSquare2 = squareDist2 * invSigmaSquare;

    if (chiSquare2 > th)
      bIn = false;
    else
      score += th - chiSquare2;

    if (bIn)
      vbMatchesInliers[i] = true;
    else
      vbMatchesInliers[i] = false;
  }

  return score;
}
// 从fundamental matrix计算symmetric transfer errors
// IV. AUTOMATIC MAP INITIALIZATION （2） in Author's paper
// symmetric transfer errors:
//    4.2.2 Geometric distance in Multiple View Geometry in Computer Vision.
// model selection
//    4.7.1 RANSAC in Multiple View Geometry in Computer Vision
float Initializer::CheckFundamental(const cv::Mat &F21, vector<bool> &vbMatchesInliers, float sigma) {
  const int N = mvMatches12.size();

  const float f11 = F21.at<float>(0, 0);
  const float f12 = F21.at<float>(0, 1);
  const float f13 = F21.at<float>(0, 2);
  const float f21 = F21.at<float>(1, 0);
  const float f22 = F21.at<float>(1, 1);
  const float f23 = F21.at<float>(1, 2);
  const float f31 = F21.at<float>(2, 0);
  const float f32 = F21.at<float>(2, 1);
  const float f33 = F21.at<float>(2, 2);

  vbMatchesInliers.resize(N);

  float score = 0;

  const float th = 3.841;
  const float thScore = 5.991;

  const float invSigmaSquare = 1.0 / (sigma * sigma);

  for (int i = 0; i < N; i++) {
    bool bIn = true;

    const cv::KeyPoint &kp1 = mvKeys1[mvMatches12[i].first];
    const cv::KeyPoint &kp2 = mvKeys2[mvMatches12[i].second];

    const float u1 = kp1.pt.x;
    const float v1 = kp1.pt.y;
    const float u2 = kp2.pt.x;
    const float v2 = kp2.pt.y;

    // Reprojection error in second image
    // l2=F21x1=(a2,b2,c2)

    const float a2 = f11 * u1 + f12 * v1 + f13;
    const float b2 = f21 * u1 + f22 * v1 + f23;
    const float c2 = f31 * u1 + f32 * v1 + f33;

    const float num2 = a2 * u2 + b2 * v2 + c2;

    const float squareDist1 = num2 * num2 / (a2 * a2 + b2 * b2);

    const float chiSquare1 = squareDist1 * invSigmaSquare;

    if (chiSquare1 > th)
      bIn = false;
    else
      score += thScore - chiSquare1;

    // Reprojection error in second image
    // l1 =x2tF21=(a1,b1,c1)

    const float a1 = f11 * u2 + f21 * v2 + f31;
    const float b1 = f12 * u2 + f22 * v2 + f32;
    const float c1 = f13 * u2 + f23 * v2 + f33;

    const float num1 = a1 * u1 + b1 * v1 + c1;

    const float squareDist2 = num1 * num1 / (a1 * a1 + b1 * b1);

    const float chiSquare2 = squareDist2 * invSigmaSquare;

    if (chiSquare2 > th)
      bIn = false;
    else
      score += thScore - chiSquare2;

    if (bIn)
      vbMatchesInliers[i] = true;
    else
      vbMatchesInliers[i] = false;
  }

  return score;
}
// 从F恢复P
// 参考文献：
// Result 9.19 in Multiple View Geometry in Computer Vision
bool Initializer::ReconstructF(vector<bool> &vbMatchesInliers, cv::Mat &F21, cv::Mat &K,
                               cv::Mat &R21, cv::Mat &t21, vector<cv::Point3f> &vP3D, vector<bool> &vbTriangulated, float minParallax, int minTriangulated) {
  int N = 0;
  for (size_t i = 0, iend = vbMatchesInliers.size() ; i < iend; i++)
    if (vbMatchesInliers[i])
      N++;

  // Compute Essential Matrix from Fundamental Matrix
  cv::Mat E21 = K.t() * F21 * K;

  cv::Mat R1, R2, t;

  // Recover the 4 motion hypotheses
  DecomposeE(E21, R1, R2, t);

  cv::Mat t1 = t;
  cv::Mat t2 = -t;

  // Reconstruct with the 4 hyphoteses and check
  vector<cv::Point3f> vP3D1, vP3D2, vP3D3, vP3D4;
  vector<bool> vbTriangulated1, vbTriangulated2, vbTriangulated3, vbTriangulated4;
  float parallax1, parallax2, parallax3, parallax4;

  int nGood1 = CheckRT(R1, t1, mvKeys1, mvKeys2, mvMatches12, vbMatchesInliers, K, vP3D1, 4.0 * mSigma2, vbTriangulated1, parallax1);
  int nGood2 = CheckRT(R2, t1, mvKeys1, mvKeys2, mvMatches12, vbMatchesInliers, K, vP3D2, 4.0 * mSigma2, vbTriangulated2, parallax2);
  int nGood3 = CheckRT(R1, t2, mvKeys1, mvKeys2, mvMatches12, vbMatchesInliers, K, vP3D3, 4.0 * mSigma2, vbTriangulated3, parallax3);
  int nGood4 = CheckRT(R2, t2, mvKeys1, mvKeys2, mvMatches12, vbMatchesInliers, K, vP3D4, 4.0 * mSigma2, vbTriangulated4, parallax4);

  int maxGood = max(nGood1, max(nGood2, max(nGood3, nGood4)));

  R21 = cv::Mat();
  t21 = cv::Mat();

  int nMinGood = max(static_cast<int>(0.9 * N), minTriangulated);

  int nsimilar = 0;
  if (nGood1 > 0.7 * maxGood)
    nsimilar++;
  if (nGood2 > 0.7 * maxGood)
    nsimilar++;
  if (nGood3 > 0.7 * maxGood)
    nsimilar++;
  if (nGood4 > 0.7 * maxGood)
    nsimilar++;

  // If there is not a clear winner or not enough triangulated points reject initialization
  if (maxGood < nMinGood || nsimilar > 1) {
    return false;
  }

  // If best reconstruction has enough parallax initialize
  if (maxGood == nGood1) {
    if (parallax1 > minParallax) {
      vP3D = vP3D1;
      vbTriangulated = vbTriangulated1;

      R1.copyTo(R21);
      t1.copyTo(t21);
      return true;
    }
  } else if (maxGood == nGood2) {
    if (parallax2 > minParallax) {
      vP3D = vP3D2;
      vbTriangulated = vbTriangulated2;

      R2.copyTo(R21);
      t1.copyTo(t21);
      return true;
    }
  } else if (maxGood == nGood3) {
    if (parallax3 > minParallax) {
      vP3D = vP3D3;
      vbTriangulated = vbTriangulated3;

      R1.copyTo(R21);
      t2.copyTo(t21);
      return true;
    }
  } else if (maxGood == nGood4) {
    if (parallax4 > minParallax) {
      vP3D = vP3D4;
      vbTriangulated = vbTriangulated4;

      R2.copyTo(R21);
      t2.copyTo(t21);
      return true;
    }
  }

  return false;
}
// 从H恢复P
// 参考文献：
// Faugeras et al, Motion and structure from motion in a piecewise planar environment. International Journal of Pattern Recognition and Artificial Intelligence, 1988.
bool Initializer::ReconstructH(vector<bool> &vbMatchesInliers, cv::Mat &H21, cv::Mat &K,
                               cv::Mat &R21, cv::Mat &t21, vector<cv::Point3f> &vP3D, vector<bool> &vbTriangulated, float minParallax, int minTriangulated) {
  int N = 0;
  for (size_t i = 0, iend = vbMatchesInliers.size() ; i < iend; i++)
    if (vbMatchesInliers[i])
      N++;

  // We recover 8 motion hypotheses using the method of Faugeras et al.
  // Motion and structure from motion in a piecewise planar environment.
  // International Journal of Pattern Recognition and Artificial Intelligence, 1988

  cv::Mat invK = K.inv();
  cv::Mat A = invK * H21 * K;

  cv::Mat U, w, Vt, V;
  cv::SVD::compute(A, w, U, Vt, cv::SVD::FULL_UV);
  V = Vt.t();

  float s = cv::determinant(U) * cv::determinant(Vt);

  float d1 = w.at<float>(0);
  float d2 = w.at<float>(1);
  float d3 = w.at<float>(2);

  if (d1 / d2 < 1.00001 || d2 / d3 < 1.00001) {
    return false;
  }

  vector<cv::Mat> vR, vt, vn;
  vR.reserve(8);
  vt.reserve(8);
  vn.reserve(8);

  //n'=[x1 0 x3] 4 posibilities e1=e3=1, e1=1 e3=-1, e1=-1 e3=1, e1=e3=-1
  float aux1 = sqrt((d1 * d1 - d2 * d2) / (d1 * d1 - d3 * d3));
  float aux3 = sqrt((d2 * d2 - d3 * d3) / (d1 * d1 - d3 * d3));
  float x1[] = {aux1, aux1, -aux1, -aux1};
  float x3[] = {aux3, -aux3, aux3, -aux3};

  //case d'=d2
  float aux_stheta = sqrt((d1 * d1 - d2 * d2) * (d2 * d2 - d3 * d3)) / ((d1 + d3) * d2);

  float ctheta = (d2 * d2 + d1 * d3) / ((d1 + d3) * d2);
  float stheta[] = {aux_stheta, -aux_stheta, -aux_stheta, aux_stheta};

  for (int i = 0; i < 4; i++) {
    cv::Mat Rp = cv::Mat::eye(3, 3, CV_32F);
    Rp.at<float>(0, 0) = ctheta;
    Rp.at<float>(0, 2) = -stheta[i];
    Rp.at<float>(2, 0) = stheta[i];
    Rp.at<float>(2, 2) = ctheta;

    cv::Mat R = s * U * Rp * Vt;
    vR.push_back(R);

    cv::Mat tp(3, 1, CV_32F);
    tp.at<float>(0) = x1[i];
    tp.at<float>(1) = 0;
    tp.at<float>(2) = -x3[i];
    tp *= d1 - d3;

    cv::Mat t = U * tp;
    vt.push_back(t / cv::norm(t));

    cv::Mat np(3, 1, CV_32F);
    np.at<float>(0) = x1[i];
    np.at<float>(1) = 0;
    np.at<float>(2) = x3[i];

    cv::Mat n = V * np;
    if (n.at<float>(2) < 0)
      n = -n;
    vn.push_back(n);
  }

  //case d'=-d2
  float aux_sphi = sqrt((d1 * d1 - d2 * d2) * (d2 * d2 - d3 * d3)) / ((d1 - d3) * d2);

  float cphi = (d1 * d3 - d2 * d2) / ((d1 - d3) * d2);
  float sphi[] = {aux_sphi, -aux_sphi, -aux_sphi, aux_sphi};

  for (int i = 0; i < 4; i++) {
    cv::Mat Rp = cv::Mat::eye(3, 3, CV_32F);
    Rp.at<float>(0, 0) = cphi;
    Rp.at<float>(0, 2) = sphi[i];
    Rp.at<float>(1, 1) = -1;
    Rp.at<float>(2, 0) = sphi[i];
    Rp.at<float>(2, 2) = -cphi;

    cv::Mat R = s * U * Rp * Vt;
    vR.push_back(R);

    cv::Mat tp(3, 1, CV_32F);
    tp.at<float>(0) = x1[i];
    tp.at<float>(1) = 0;
    tp.at<float>(2) = x3[i];
    tp *= d1 + d3;

    cv::Mat t = U * tp;
    vt.push_back(t / cv::norm(t));

    cv::Mat np(3, 1, CV_32F);
    np.at<float>(0) = x1[i];
    np.at<float>(1) = 0;
    np.at<float>(2) = x3[i];

    cv::Mat n = V * np;
    if (n.at<float>(2) < 0)
      n = -n;
    vn.push_back(n);
  }


  int bestGood = 0;
  int secondBestGood = 0;
  int bestSolutionIdx = -1;
  float bestParallax = -1;
  vector<cv::Point3f> bestP3D;
  vector<bool> bestTriangulated;

  // Instead of applying the visibility constraints proposed in the Faugeras' paper (which could fail for points seen with low parallax)
  // We reconstruct all hypotheses and check in terms of triangulated points and parallax
  for (size_t i = 0; i < 8; i++) {
    float parallaxi;
    vector<cv::Point3f> vP3Di;
    vector<bool> vbTriangulatedi;
    int nGood = CheckRT(vR[i], vt[i], mvKeys1, mvKeys2, mvMatches12, vbMatchesInliers, K, vP3Di, 4.0 * mSigma2, vbTriangulatedi, parallaxi);

    if (nGood > bestGood) {
      secondBestGood = bestGood;
      bestGood = nGood;
      bestSolutionIdx = i;
      bestParallax = parallaxi;
      bestP3D = vP3Di;
      bestTriangulated = vbTriangulatedi;
    } else if (nGood > secondBestGood) {
      secondBestGood = nGood;
    }
  }


  if (secondBestGood < 0.75 * bestGood && bestParallax >= minParallax && bestGood > minTriangulated && bestGood > 0.9 * N) {
    vR[bestSolutionIdx].copyTo(R21);
    vt[bestSolutionIdx].copyTo(t21);
    vP3D = bestP3D;
    vbTriangulated = bestTriangulated;

    return true;
  }

  return false;
}

void Initializer::Triangulate(const cv::KeyPoint &kp1, const cv::KeyPoint &kp2, const cv::Mat &P1, const cv::Mat &P2, cv::Mat &x3D) {
  cv::Mat A(4, 4, CV_32F);

  A.row(0) = kp1.pt.x * P1.row(2) - P1.row(0);
  A.row(1) = kp1.pt.y * P1.row(2) - P1.row(1);
  A.row(2) = kp2.pt.x * P2.row(2) - P2.row(0);
  A.row(3) = kp2.pt.y * P2.row(2) - P2.row(1);

  cv::Mat u, w, vt;
  cv::SVD::compute(A, w, u, vt, cv::SVD::MODIFY_A | cv::SVD::FULL_UV);
  x3D = vt.row(3).t();
  x3D = x3D.rowRange(0, 3) / x3D.at<float>(3);
}
// 归一化特征点到同一尺度（作为normalize DLT的输入）
void Initializer::Normalize(const vector<cv::KeyPoint> &vKeys, vector<cv::Point2f> &vNormalizedPoints, cv::Mat &T) {
  float meanX = 0;
  float meanY = 0;
  const int N = vKeys.size();

  vNormalizedPoints.resize(N);

  for (int i = 0; i < N; i++) {
    meanX += vKeys[i].pt.x;
    meanY += vKeys[i].pt.y;
  }

  meanX = meanX / N;
  meanY = meanY / N;

  float meanDevX = 0;
  float meanDevY = 0;

  for (int i = 0; i < N; i++) {
    vNormalizedPoints[i].x = vKeys[i].pt.x - meanX;
    vNormalizedPoints[i].y = vKeys[i].pt.y - meanY;

    meanDevX += fabs(vNormalizedPoints[i].x);
    meanDevY += fabs(vNormalizedPoints[i].y);
  }

  meanDevX = meanDevX / N;
  meanDevY = meanDevY / N;

  float sX = 1.0 / meanDevX;
  float sY = 1.0 / meanDevY;

  for (int i = 0; i < N; i++) {
    vNormalizedPoints[i].x = vNormalizedPoints[i].x * sX;
    vNormalizedPoints[i].y = vNormalizedPoints[i].y * sY;
  }

  T = cv::Mat::eye(3, 3, CV_32F);
  T.at<float>(0, 0) = sX;
  T.at<float>(1, 1) = sY;
  T.at<float>(0, 2) = -meanX * sX;
  T.at<float>(1, 2) = -meanY * sY;
}


int Initializer::CheckRT(const cv::Mat &R, const cv::Mat &t, const vector<cv::KeyPoint> &vKeys1, const vector<cv::KeyPoint> &vKeys2,
                         const vector<Match> &vMatches12, vector<bool> &vbMatchesInliers,
                         const cv::Mat &K, vector<cv::Point3f> &vP3D, float th2, vector<bool> &vbGood, float &parallax) {
  // Calibration parameters
  const float fx = K.at<float>(0, 0);
  const float fy = K.at<float>(1, 1);
  const float cx = K.at<float>(0, 2);
  const float cy = K.at<float>(1, 2);

  vbGood = vector<bool>(vKeys1.size(), false);
  vP3D.resize(vKeys1.size());

  vector<float> vCosParallax;
  vCosParallax.reserve(vKeys1.size());

  // Camera 1 Projection Matrix K[I|0]
  cv::Mat P1(3, 4, CV_32F, cv::Scalar(0));
  K.copyTo(P1.rowRange(0, 3).colRange(0, 3));

  cv::Mat O1 = cv::Mat::zeros(3, 1, CV_32F);

  // Camera 2 Projection Matrix K[R|t]
  cv::Mat P2(3, 4, CV_32F);
  R.copyTo(P2.rowRange(0, 3).colRange(0, 3));
  t.copyTo(P2.rowRange(0, 3).col(3));
  P2 = K * P2;

  cv::Mat O2 = -R.t() * t;

  int nGood = 0;

  for (size_t i = 0, iend = vMatches12.size(); i < iend; i++) {
    if (!vbMatchesInliers[i])
      continue;

    const cv::KeyPoint &kp1 = vKeys1[vMatches12[i].first];
    const cv::KeyPoint &kp2 = vKeys2[vMatches12[i].second];
    cv::Mat p3dC1;

    Triangulate(kp1, kp2, P1, P2, p3dC1);

    if (!isfinite(p3dC1.at<float>(0)) || !isfinite(p3dC1.at<float>(1)) || !isfinite(p3dC1.at<float>(2))) {
      vbGood[vMatches12[i].first] = false;
      continue;
    }

    // Check parallax
    cv::Mat normal1 = p3dC1 - O1;
    float dist1 = cv::norm(normal1);

    cv::Mat normal2 = p3dC1 - O2;
    float dist2 = cv::norm(normal2);

    float cosParallax = normal1.dot(normal2) / (dist1 * dist2);

    // Check depth in front of first camera (only if enough parallax, as "infinite" points can easily go to negative depth)
    if (p3dC1.at<float>(2) <= 0 && cosParallax < 0.99998)
      continue;

    // Check depth in front of second camera (only if enough parallax, as "infinite" points can easily go to negative depth)
    cv::Mat p3dC2 = R * p3dC1 + t;

    if (p3dC2.at<float>(2) <= 0 && cosParallax < 0.99998)
      continue;

    // Check reprojection error in first image
    float im1x, im1y;
    float invZ1 = 1.0 / p3dC1.at<float>(2);
    im1x = fx * p3dC1.at<float>(0) * invZ1 + cx;
    im1y = fy * p3dC1.at<float>(1) * invZ1 + cy;

    float squareError1 = (im1x - kp1.pt.x) * (im1x - kp1.pt.x) + (im1y - kp1.pt.y) * (im1y - kp1.pt.y);

    if (squareError1 > th2)
      continue;

    // Check reprojection error in second image
    float im2x, im2y;
    float invZ2 = 1.0 / p3dC2.at<float>(2);
    im2x = fx * p3dC2.at<float>(0) * invZ2 + cx;
    im2y = fy * p3dC2.at<float>(1) * invZ2 + cy;

    float squareError2 = (im2x - kp2.pt.x) * (im2x - kp2.pt.x) + (im2y - kp2.pt.y) * (im2y - kp2.pt.y);

    if (squareError2 > th2)
      continue;

    vCosParallax.push_back(cosParallax);
    vP3D[vMatches12[i].first] = cv::Point3f(p3dC1.at<float>(0), p3dC1.at<float>(1), p3dC1.at<float>(2));
    nGood++;

    if (cosParallax < 0.99998)
      vbGood[vMatches12[i].first] = true;
  }

  if (nGood > 0) {
    sort(vCosParallax.begin(), vCosParallax.end());

    size_t idx = min(50, int(vCosParallax.size() - 1));
    parallax = acos(vCosParallax[idx]) * 180 / CV_PI;
  } else
    parallax = 0;

  return nGood;
}

void Initializer::DecomposeE(const cv::Mat &E, cv::Mat &R1, cv::Mat &R2, cv::Mat &t) {
  cv::Mat u, w, vt;
  cv::SVD::compute(E, w, u, vt);

  u.col(2).copyTo(t);
  t = t / cv::norm(t);

  cv::Mat W(3, 3, CV_32F, cv::Scalar(0));
  W.at<float>(0, 1) = -1;
  W.at<float>(1, 0) = 1;
  W.at<float>(2, 2) = 1;

  R1 = u * W * vt;
  if (cv::determinant(R1) < 0)
    R1 = -R1;

  R2 = u * W.t() * vt;
  if (cv::determinant(R2) < 0)
    R2 = -R2;
}

} //namespace ORB_SLAM

 

该系列的其它文章：

ORB－SLAM（一）简介

ORB－SLAM（二）性能

ORB－SLAM（四）追踪

ORB－SLAM（五）优化

ORB－SLAM（六）回环检测