图的遍历、拓扑排序、最短路径算法
深度优先搜索算法（Depth-First-Search），是搜索算法的一种。它沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所有边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。DFS 属于盲目搜索。
深度优先搜索是图论中的经典算法，利用深度优先搜索算法可以产生目标图的相应拓扑排序表，利用拓扑排序表可以方便的解决很多相关的图论问题，如最大路径问题等等。一般用堆数据结构来辅助实现 DFS 算法。
深度优先遍历图算法步骤：
1. 访问顶点v；
2. 依次从v的未被访问的邻接点出发，对图进行深度优先遍历；直至图中和v有路径相通的顶点都被访问；
3. 若此时图中尚有顶点未被访问，则从一个未被访问的顶点出发，重新进行深度优先遍历，直到图中所有顶点均被访问过为止。
上述描述可能比较抽象，举个实例：
DFS 在访问图中某一起始顶点 v 后，由 v 出发，访问它的任一邻接顶点 w1；再从 w1 出发，访问与 w1 邻 接但还没有访问过的顶点 w2；然后再从 w2 出发，进行类似的访问，… 如此进行下去，直至到达所有的邻接顶点都被访问过的顶点 u 为止。
接着，退回一步，退到前一次刚访问过的顶点，看是否还有其它没有被访问的邻接顶点。如果有，则访问此顶点，之后再从此顶点出发，进行与前述类似的访问；如果没有，就再退回一步进行搜索。重复上述过程，直到连通图中所有顶点都被访问过为止。
//深度优先遍历： void DFSTraverse ( Graph G ) { visited [0 .. G.vexnum-1] = false; // 初始化访问标志为未访问(false) for ( v = 0; v < G.vexnum; v ++ ) if ( ! visited[v] ) DFS ( G, v ); // 从未被访问的顶点开始DFS } void DFS ( Graph G, int v ) { visit ( v ); visited [v] = true; // 访问顶点v并作标记 for ( w = FirstAdjVex(G,v); w >= 0; w = NextAdjVex(G,v,w) ) if ( ! visited[w] ) DFS ( G, w ); // 分别从每个未访问的邻接点开始DFS }
Order in which the nodes are visited (one example).
2.BFS (广度优先搜索)
广度优先搜索算法（Breadth-First-Search），是一种图形搜索算法。简单的说，BFS 是从根节点开始，沿着树(图)的宽度遍历树(图)的节点。如果所有节点均被访问，则算法中止。BFS 同样属于盲目搜索。一般用队列数据结构来辅助实现 BFS 算法。
算法步骤：
1. 首先将根节点放入队列中。
2. 从队列中取出第一个节点，并检验它是否为目标。
- 如果找到目标，则结束搜寻并回传结果。
- 否则将它所有尚未检验过的直接子节点加入队列中。
3. 若队列为空，表示整张图都检查过了——亦即图中没有欲搜寻的目标。结束搜寻并回传“找不到目标”。
4. 重复步骤2。
//广度优先遍历：利用队列(类似按层遍历二叉树)。 void BFSTraverse ( Graph G ) { visited [0 .. G.vexnum-1] = false; // 初始化访问标志为未访问(false) InitQueue ( Q ); for ( v = 0; v < G.vexnum; v++ ) if ( ! visited[v] ) { // 从v出发广度优先搜索 visit ( v ); visited [v] = true; EnQueue ( Q, v ); while ( ! QueueEmpty(Q) ) { DeQueue ( Q, u ); for ( w = FirstAdjVex(G,u); w >= 0; w = NextAdjVex(G,u,w) ) if ( ! visited[w] ) { visit ( w ); visited [w] = true; EnQueue ( Q, w ); } } } }
3.拓扑排序（topological sort）
//拓扑排序：可以测试一个有向图是否有环 void Graph::topsort( ) { Queue<Vertex> q; int counter = 0; q.makeEmpty( ); for each Vertex v if( v.indegree == 0 ) q.enqueue( v ); while( !q.isEmpty( ) ) { Vertex v = q.dequeue( ); v.topNum = ++counter; // Assign next number for each Vertex w adjacent to v if( --w.indegree == 0 ) q.enqueue( w ); } if( counter != NUM_VERTICES ) throw CycleFoundException( ); }
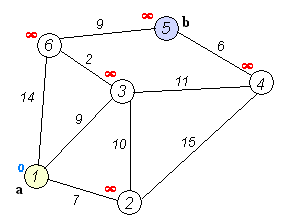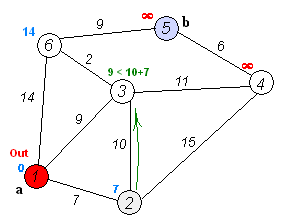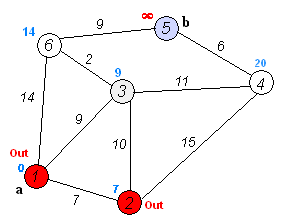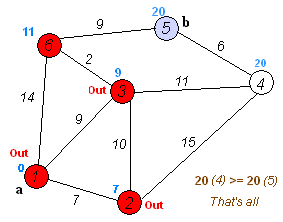
4.Dijkstra算法(Dijkstra's algorithm)
迪杰斯特拉算法（Dijkstra’s algorithm）是由荷兰计算机科学家艾兹赫尔·迪杰斯特拉提出。迪杰斯特拉算法使用了广度优先搜索解决非负权有向图的单源最短路径问题，算法最终得到一个最短路径树。该算法常用于路由算法或者作为其他图算法的一个子模块。
该算法的输入包含了一个有权重的有向图 G，以及G中的一个来源顶点 S。我们以 V 表示 G 中所有顶点的集合。每一个图中的边，都是两个顶点所形成的有序元素对。(u, v) 表示从顶点 u 到 v 有路径相连。我们以 E 表示G中所有边的集合，而边的权重则由权重函数 w: E → [0, ∞] 定义。因此，w(u, v) 就是从顶点 u 到顶点 v 的非负权重（weight）。边的权重可以想像成两个顶点之间的距离。任两点间路径的权重，就是该路径上所有边的权重总和。已知有 V 中有顶点 s 及 t，Dijkstra 算法可以找到 s 到 t的最低权重路径(例如，最短路径)。这个算法也可以在一个图中，找到从一个顶点 s 到任何其他顶点的最短路径。对于不含负权的有向图，Dijkstra 算法是目前已知的最快的单源最短路径算法。
算法步骤：
1. 初始时令 S={V0},T={其余顶点}，T中顶点对应的距离值
若存在<V0,Vi>，d(V0,Vi)为<V0,Vi>弧上的权值
若不存在<V0,Vi>，d(V0,Vi)为∞
2. 从T中选取一个其距离值为最小的顶点W且不在S中，加入S
3. 对其余T中顶点的距离值进行修改：若加进W作中间顶点，从 V0 到 Vi 的距离值缩短，则修改此距离值
重复上述步骤2、3，直到S中包含所有顶点，即W=Vi 为止
算法实现：
/*迪杰斯特拉算法： 求一个顶点到其他各顶点的最短路径。 算法： (a) 初始化：用起点v到该顶点w的直接边(弧)初始化最短路径，否则设为∞； (b) 从未求得最短路径的终点中选择路径长度最小的终点u：即求得v到u的最短路径； (c) 修改最短路径：计算u的邻接点的最短路径，若(v,…,u)+(u,w)<(v,…,w)，则以(v,…,u,w)代替。 (d) 重复(b)-(c)，直到求得v到其余所有顶点的最短路径。 特点：总是按照从小到大的顺序求得最短路径。 */ //单源最短路径dijkstra算法：s点到其他各顶点的最短路径 void Graph::dijkstra( Vertex s ) { for each Vertex v { v.dist = INFINITY; v.known = false; } s.dist = 0; for( ; ; ) { Vertex v = smallest unknown distance vertex; if( v == NOT_A_VERTEX ) break; v.known = true; for each Vertex w adjacent to v if( !w.known ) if( v.dist + cvw < w.dist ) { // Update w w.dist = v.dist + cvw; w.path = v; } } }
5.权值为1的单源最短路径
//图边的权值为1，最短路径：s点到其他各顶点的最短路径 void Graph::unweighted( Vertex s ) { for each Vertex v { v.dist = INFINITY; v.known = false; } s.dist = 0; for( int currDist = 0; currDist < NUM_VERTICES; currDist++ ) for each Vertex v if( !v.known && v.dist == currDist ) { v.known = true; for each Vertex w adjacent to v if( w.dist == INFINITY ) { w.dist = currDist + 1; w.path = v; } } }
使用队列queue实现：
//图边的权值为1，最短路径：s点到其他各顶点的最短路径 void Graph::unweighted( Vertex s ) { Queue<Vertex> q; for each Vertex v v.dist = INFINITY; s.dist = 0; q.enqueue( s ); while( !q.isEmpty( ) ) { Vertex v = q.dequeue( ); for each Vertex w adjacent to v if( w.dist == INFINITY ) { w.dist = v.dist + 1; w.path = v; q.enqueue( w ); } } }
6.有负边值的加权最短路径
//有负边值的加权最短路径算法 void Graph::weightedNegative( Vertex s ) { Queue<Vertex> q; for each Vertex v v.dist = INFINITY; s.dist = 0; q.enqueue( s ); while( !q.isEmpty( ) ) { Vertex v = q.dequeue( ); for each Vertex w adjacent to v if( v.dist + cvw < w.dist ) { // Update w w.dist = v.dist + cvw; w.path = v; if( w is not already in q ) q.enqueue( w ); } } }
7.计算任意两点间的最短路径
/** * Compute all-shortest paths. * a contains the adjacency matrix with a[ i ][ i ] presumed to be zero. * d contains the values of the shortest path. * Vertices are numbered starting at 0; all arrays have equal dimension. * A negative cycle exists if d[ i ][ i ] is set to a negative value. * Actual path can be computed using path[ ][ ]. * NOT_A_VERTEX is -1 */ void allPairs( const matrix<int> & a, matrix<int> & d, matrix<int> & path ) { int n = a.numrows( ); // Initialize d and path for( int i = 0; i < n; i++ ) for( int j = 0; j < n; j++ ) { d[ i ][ j ] = a[ i ][ j ]; path[ i ][ j ] = NOT_A_VERTEX; } for( int k = 0; k < n; k++ ) // Consider each vertex as an intermediate for( int i = 0; i < n; i++ ) for( int j = 0; j < n; j++ ) if( d[ i ][ k ] + d[ k ][ j ] < d[ i ][ j ] ) { // Update shortest path d[ i ][ j ] = d[ i ][ k ] + d[ k ][ j ]; path[ i ][ j ] = k; } }
