6.1 图的深度优先和广度优先搜索
图的广度优先搜索
图的的搜索算法主要分为广度优先搜索(breadth-first search或BFS)和深度优先搜索(depth-first search或DFS)。首先讨论广度优先搜索算法。
称之为广度优先,是因为算法始终首先发现距离起始顶点较近的顶点,然后才发现较远的顶点。假设搜索的出发顶点为s,则首先搜索与s直接相邻的顶点,然后再搜索这些相邻顶点的相邻顶点。在搜索过程中可以记录每个顶点到起始顶点s的距离。这种搜索算法能生成一棵以s为根、包括所有s可达的顶点的广度优先搜索树(BFS树)。图中各顶点的访问次序对应于广度优先搜索树中各节点由顶至底的层次。
在这里我们设计算法跟踪图中各个顶点的访问次序,记录各个顶点在BFS树中的层数(搜索深度)以及父顶点。首先将各个顶点着白色,在跟踪各个顶点访问次序时,第一次被访问的顶点的颜色改变为灰色,直至与之相邻的所有顶点都被访问时颜色改变为黑色。在这个过程中颜色为黑色和白色的顶点之间被颜色为灰色的顶点分割开来。广度优先搜索算法的实现借助于队列结构,代码如下:
* 广度优先搜索算法,从第start节点开始进行搜索;
* 算法中利用到队列数据结构。
* @param G 待搜索的图
* @param start 搜索的起点
*/
static void BFS(GraphLnk G, int start){
int n = G.get_nv();
if(start < 0 || start >= n) return;
color = new COLOR[n];
// 节点的父节点,非负整数
parent = new int[n];
// 深度depth
d = new int[n];
// 初始化
for(int i = 0; i < n; i++){
//将所有顶点的颜色着色为白色
color[i] = COLOR.WHITE;
//所有顶点的父母初始化为-1
parent[i] = -1;
//所有顶点的深度初始化为无穷大
d[i] = Integer.MAX_VALUE;
}
// 起点着色为灰色
color[start] = COLOR.GRAY;
// 起点无父节点,记为-1
parent[start] = -1;
// 起点的深度为0
d[start] = 0;
// 创建队列
LinkQueue Q = new LinkQueue();
//将起点添加到队列中
Q.enqueue(new ElemItem<Integer>(start));
// 迭代第对队列首顶点的相邻边重新着色
while(Q.currSize() > 0){
// 队列首顶点u
int u = ((Integer)(Q.dequeue().elem)).intValue();
for(Edge w = G.firstEdge(u);
G.isEdge(w);
w = G.nextEdge(w)){
/* 如果u的相邻顶点第一次被发现了,则将其颜色改变为灰色,
* 其深度增加1,其父顶点为u,并将该顶点添加到队列 */
if(color[w.get_v2()] == COLOR.WHITE){
color[w.get_v2()] = COLOR.GRAY;
d[w.get_v2()] = d[u] + 1;
parent[w.get_v2()] = u;
Q.enqueue(new ElemItem<Integer>(w.get_v2()));
}
}
// 搜索了顶点u的所有相邻顶点后,将其颜色改变为黑色
color[u] = COLOR.BLACK;
// 打印此时各个顶点的颜色
for(int i = 0; i < n; i++){
System.out.print(i + ")" + color[i] + "\t");
}
System.out.println();
}
// 打印所有顶点的搜索深度
System.out.println("各顶点的深度为:");
for(int i = 0; i < n; i++){
System.out.print(d[i] + "\t");
}
// 打印所有顶点的父顶点
System.out.println("\n各顶点的父母为:");
for(int i = 0; i < n; i++){
System.out.print(parent[i] + "\t");
}
System.out.println();
}
从函数的实现可以发现,广度优先搜索算法是迭代实现的。迭代过程借助队列结构暂存着灰色的顶点。首先访问顶点s,并将与其相邻的、未访问过的顶点都添加到队列中;然后迭代地将队列中顶点弹出、对其访问,并将与其相邻的、未访问过的顶点添加到队列中。在前面章节我们讨论过,队列中元素项遵循先入先出(FIFO)的规则;迭代直至队列为空为止。在BFS算法中FIFO规则保证了图中顶点的访问次序:先访问的顶点距离起始顶点更近。
依然以图(a)为例来分析广度优先算法的过程以及广度优先树的意义,搜索的起点为顶点1。测试示例代码为:
GraphLnk GL =
Utilities.BulidGraphLnkFromFile("Graph\\graph1.txt");
GraphSearch.BFS(GL, 1);
运行结果为:
0)GRAY1)BLACK2)WHITE3)WHITE4)WHITE5)GRAY6)WHITE7)WHITE
0)BLACK1)BLACK2)WHITE3)WHITE4)GRAY5)GRAY6)WHITE7)WHITE
0)BLACK1)BLACK2)GRAY3)WHITE4)GRAY5)BLACK6)GRAY7)WHITE
0)BLACK1)BLACK2)GRAY3)WHITE4)BLACK5)BLACK6)GRAY7)WHITE
0)BLACK1)BLACK2)BLACK3)GRAY4)BLACK5)BLACK6)GRAY7)WHITE
0)BLACK1)BLACK2)BLACK3)GRAY4)BLACK5)BLACK6)BLACK7)GRAY
0)BLACK1)BLACK2)BLACK3)BLACK4)BLACK5)BLACK6)BLACK7)GRAY
0)BLACK1)BLACK2)BLACK3)BLACK4)BLACK5)BLACK6)BLACK7)BLACK
各顶点的深度为:
10232123
各顶点的父母为:
1-1520156
搜索过程中各顶点颜色及队列中灰色顶点的变化过程如图(1~8),每张图对应队列中元素变化时的状态。
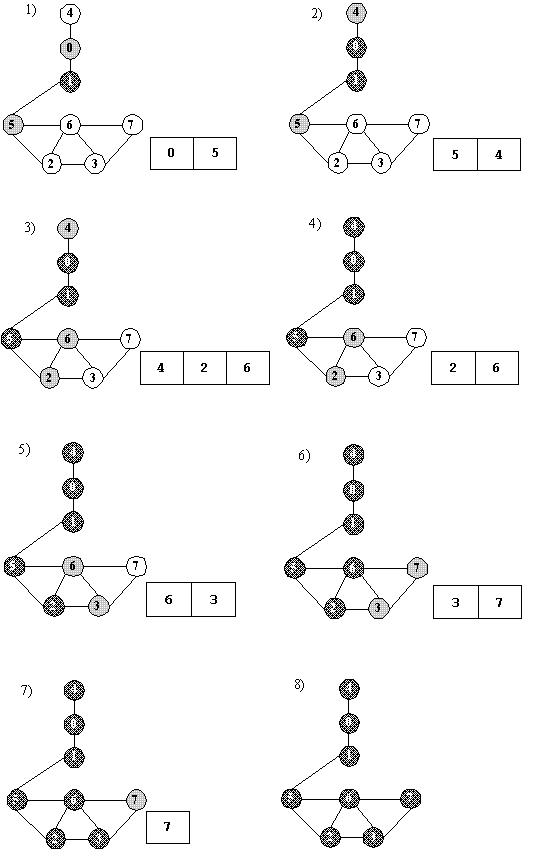
图 广度优先搜索过程
根据广度优先搜索算法得出的个顶点到起始点的距离可以得出广度优先搜索树如下:

图 BFS树
广度优先搜索算法可以得到从给定起始顶点到每个可达顶点的距离,并且这个距离是顶点到起始顶点的最短路径,具体的证明过程请参阅相关图论数据。
. 图的深度优先搜索
图的另一种搜索算法称为深度优先搜索(DFS),正如算法的名称那样,DFS算法总是尽可能“深”地搜索图。在DFS过程中,某个顶点v在被访问后,将递归地访问第一个尚未被访问过的相邻点,直至没有相邻点可访问为止;然后再回溯到顶点v,继续递归访问v的第二个尚未访问过的相邻点。这一过程一直进行到已访问了起点可达的所有顶点为止。
除了递归方式之外,还可以借助堆栈采用迭代方式实现。首先访问起点v,然后把顶点v及其相连的边压入栈中;弹出并访问栈顶元素,栈顶元素对应的边的另一顶点就是下一个访问的顶点,对其重复顶点v的操作;迭代过程直至栈中没有元素为止。
无论采用递归方式还是采用迭代方式,其结果都是首先沿着图的一条路径搜索直至它的末端,然后回溯,并沿着另一路径搜索。这里我们主要实现DFS算法的递归方式。
在图的广度优先搜索算法中我们记录了图中每个顶点的深度,并在搜索过程中对各顶点进行着色的变化。在深度优先搜索算法中,我们将同时记录访问顶点的两个时间(次序),第一个是开始访问顶点的时间d,另一个是访问完该顶点的所有相邻顶点的时间f。根据这两个时间的定义,对于顶点v,在时间dv之前顶点v一直为白色,在时间dv到fv之间顶点v为灰色,fv之后顶点为黑色。
深度优先搜索算法实现如下:
* 深度优先搜索算法,从第start个节点开始搜索
* @param G 待搜索的图
* @param start 搜索起点
*/
static void DFS(GraphLnk G, int start){
int n = G.get_nv();
// 时间戳更新计数器置0
time = 0;
if(start < 0 || start >= n)
return;
// 各顶点的着色
color = new COLOR[n];
// 节点的父节点,非负整数
parent = new int[n];
// 第一个时间戳
d = new int[n];
// 第二个时间戳
f = new int[n];
// 每个节点的访问次序
ord = new int[n];
// 初始化
for(int i = 0; i < n; i++){
//将所有顶点的颜色着色为白色
color[i] = COLOR.WHITE;
//所有顶点的父母初始化为-1
parent[i] = -1;
//所有顶点的深度初始化为无穷大
d[i] = Integer.MAX_VALUE;
f[i] = Integer.MAX_VALUE;
//节点个访问次序都初始设为-1
ord[i] = -1;
}
//调用递归函数,进行遍历访问
DFS_VISIT(G, start);
}
函数DFS首先对个顶点颜色、两个时间值以及访问次序等值进行初始化,然后调用递归函数DFS_VISIT对图中顶点进行深度优先搜索。DFS函数有两种版本,一种规定搜索的其实顶点,即上面的代码,这种实现只能搜索到给定顶点能到达的所有顶点;另一种不规定起点,这样能适用于有分离的子图构成的图的遍历。下面具体讨论递归遍历函数DFS_VISIT,函数的实现如下:
* 深度优先搜索算法中调用的递归函数,
* 实现图的递归遍历
* @param G 待搜索的图
* @param u 搜索的起点
*/
static int k = 0;
public static void DFS_VISIT(Graph G, int u){
// 起点u首先着色为灰色
color[u] = COLOR.GRAY;
// 顶点的访问时间增加1
time++;
d[u] = time;
// 打印所有顶点的颜色
for(int i = 0; i < G.get_nv(); i++){
System.out.print(i + ")" + color[i] + "\t");
}
System.out.println();
// 打印并显示每个顶点的深度和父顶点
for(int i = 0; i < G.get_nv(); i++){
String _4print = "";
if(d[i] < Integer.MAX_VALUE
&& f[i] < Integer.MAX_VALUE)
_4print = i + ")" + d[i] + "/" + f[i] + "\t";
else if(d[i] < Integer.MAX_VALUE)
_4print = i + ")" + d[i] + "/" + "\t";
else
_4print = i + ")" + " " + "/" + " " + "\t";
System.out.print(_4print);
}
System.out.println();
// 递归搜索顶点u的所有尚未访问过的相邻顶点
for(Edge w = G.firstEdge(u);
G.isEdge(w);
w = G.nextEdge(w)){
if(color[w.get_v2()] == COLOR.WHITE){
parent[w.get_v2()] = u;
DFS_VISIT(G, w.get_v2());
}
}
// 将u其颜色改变为黑色
color[u] = COLOR.BLACK;
// 顶点访问结束时的时间
f[u] = ++time;
// 顶点被访问的次序
ord[u] = k++;
// 打印各个顶点的颜色
for(int i = 0; i < G.get_nv(); i++){
System.out.print(i + ")" + color[i] + "\t");
}
System.out.println();
// 打印各个顶点被访问的起始、结束时间
for(int i = 0; i < G.get_nv(); i++){
String _4print = "";
if(d[i] < Integer.MAX_VALUE
&& f[i] < Integer.MAX_VALUE)
_4print = i + ")" + d[i] + "/" + f[i] + "\t";
else if(d[i] < Integer.MAX_VALUE)
_4print = i + ")" + d[i] + "/" + "\t";
else
_4print = i + ")" + " " + "/" + " " + "\t";
System.out.print(_4print);
}
System.out.println();
}
DFS_VISIT函数在执行时首先对本次递归调用的时间值time进行更新,将其作为入参顶点u的第一时间d[u];然后将顶点u的颜色重置为灰色。函数关键的步骤为递归地对搜索顶点u的每一个相邻顶点,首先搜索第一个尚未被访问的相邻点,然后回溯至顶点u并递归搜索第二个尚未被访问的相邻点。如果顶点的相邻顶点为白色,则该顶点尚未被访问。顶点u的所有相邻顶点都被访问后将u顶点的着色重置为黑色,并记录第二个时间f[u]为此时的时间time。
以有向图图(b)为例来分析深度优先算法的过程,测试两种遍历过程,第一种设定搜索的起点为顶点0,搜索顶点0能到达的所有顶点;第二种不设定顶点,搜索图中所有顶点。有向图的边信息如下:
6
0,1,1
0,3,1
1,4,1
2,4,1
2,5,1
3,1,1
4,3,1
5,5,1
测试示例代码为:
Utilities.BulidGraphLnkFromFile("Graph\\graph2.txt");
System.out.println("顶点0作为起点深度优先搜索结果:");
GraphSearch.DFS(GL, 0);
System.out.println();
System.out.println("无起始顶点深度优先搜索结果:");
GraphSearch.DFS(GL);
运行结果为:
顶点0作为起点深度优先搜索结果:
0)GRAY1)WHITE2)WHITE3)WHITE4)WHITE5)WHITE
0)1/1) / 2) / 3) / 4) / 5) /
0)GRAY1)GRAY2)WHITE3)WHITE4)WHITE5)WHITE
0)1/1)2/2) / 3) / 4) / 5) /
0)GRAY1)GRAY2)WHITE3)WHITE4)GRAY5)WHITE
0)1/1)2/2) / 3) / 4)3/5) /
0)GRAY1)GRAY2)WHITE3)GRAY4)GRAY5)WHITE
0)1/1)2/2) / 3)4/4)3/5) /
0)GRAY1)GRAY2)WHITE3)BLACK4)GRAY5)WHITE
0)1/1)2/2) / 3)4/54)3/5) /
0)GRAY1)GRAY2)WHITE3)BLACK4)BLACK5)WHITE
0)1/1)2/2) / 3)4/54)3/65) /
0)GRAY1)BLACK2)WHITE3)BLACK4)BLACK5)WHITE
0)1/1)2/72) / 3)4/54)3/65) /
0)BLACK1)BLACK2)WHITE3)BLACK4)BLACK5)WHITE
0)1/81)2/72) / 3)4/54)3/65) /
无起始顶点深度优先搜索结果:
0)GRAY1)WHITE2)WHITE3)WHITE4)WHITE5)WHITE
0)1/1) / 2) / 3) / 4) / 5) /
0)GRAY1)GRAY2)WHITE3)WHITE4)WHITE5)WHITE
0)1/1)2/2) / 3) / 4) / 5) /
0)GRAY1)GRAY2)WHITE3)WHITE4)GRAY5)WHITE
0)1/1)2/2) / 3) / 4)3/5) /
0)GRAY1)GRAY2)WHITE3)GRAY4)GRAY5)WHITE
0)1/1)2/2) / 3)4/4)3/5) /
0)GRAY1)GRAY2)WHITE3)BLACK4)GRAY5)WHITE
0)1/1)2/2) / 3)4/54)3/5) /
0)GRAY1)GRAY2)WHITE3)BLACK4)BLACK5)WHITE
0)1/1)2/2) / 3)4/54)3/65) /
0)GRAY1)BLACK2)WHITE3)BLACK4)BLACK5)WHITE
0)1/1)2/72) / 3)4/54)3/65) /
0)BLACK1)BLACK2)WHITE3)BLACK4)BLACK5)WHITE
0)1/81)2/72) / 3)4/54)3/65) /
0)BLACK1)BLACK2)GRAY3)BLACK4)BLACK5)WHITE
0)1/81)2/72)9/3)4/54)3/65) /
0)BLACK1)BLACK2)GRAY3)BLACK4)BLACK5)GRAY
0)1/81)2/72)9/3)4/54)3/65)10/
0)BLACK1)BLACK2)GRAY3)BLACK4)BLACK5)BLACK
0)1/81)2/72)9/3)4/54)3/65)10/11
0)BLACK1)BLACK2)BLACK3)BLACK4)BLACK5)BLACK
0)1/81)2/72)9/123)4/54)3/65)10/11
结果中每两行为一个状态,第一行为个顶点的颜色,第二行为个顶点的两个时间:d[u]/f[u]。程序运行流程如下:
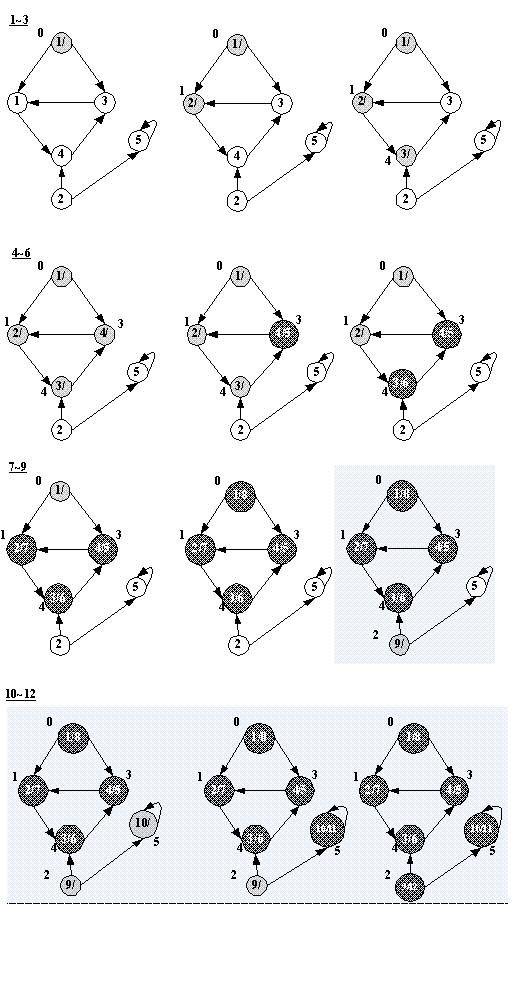
设定起始顶点为0时,算法只能搜索到图中顶点0可到达的所有顶点,即顶点1,4,3,其过程为上图步骤1~8。不设定起始顶点时,可以搜索到图中所有顶点。
前面我们提到,深度优先搜索所获得每个顶点的两个时间d和f蕴含了图的结构信息,即所谓的“括号对结构”(parenthesis structure)。根据最终得到的各顶点的时间d和时间f,可以得到如图(a, b)所示的括号结构,其中图(b)中对各顶点的位置做了调整。
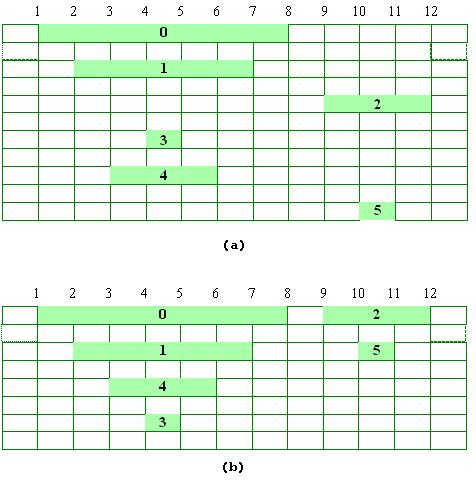
图 深度优先搜索算法得到的括号对结构
另一方面,根据算法获得的各顶点的父顶点数组parent[],可以构造深度优先搜索森林。对图(b)所有顶点进行深度优先搜索得到的父顶点数组为:
-1, 0, -1, 4, 1, 2,
可以构造出如图所示的深度优先森林。可以发现括号对结构和深度优先森林之间存在对应关系。如果顶点v和顶点u的搜索访问时间满足条件d[u]<d[v]<f[v]<d[u],那么顶点v必然是顶点u的后裔。具体证明请读者参阅相关图论书籍。
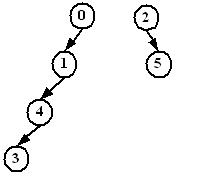
图 深度优先森林
广度优先搜索和深度优先搜索算法将多次应用到下面即将介绍的算法中。

