特征值与特征向量
一 定义
假设矩阵A为n*n方阵,x为n*1向量,则y=Ax表示矩阵A对向量x的线性变换结果,由于A为n*n方阵,则y为n*1向量。对大多数x进行线性变换,得到向量y与原向量x一般都不共线,只有少数向量x满足 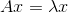 ,其中
,其中  被称为矩阵A的特征值,x 被称为矩阵A的特征向量。
被称为矩阵A的特征值,x 被称为矩阵A的特征向量。
为了求解特征值  与特征向量 x, 对上式改写为
与特征向量 x, 对上式改写为  ,则特征向量在
,则特征向量在  零空间中,通过选取一定特征值使得矩阵
零空间中,通过选取一定特征值使得矩阵  为奇异矩阵,即
为奇异矩阵,即  。根据矩阵行列式计算公式,得到关于
。根据矩阵行列式计算公式,得到关于  的n次方程,然后根据计算出的特征值,通过寻找矩阵
的n次方程,然后根据计算出的特征值,通过寻找矩阵  的零空间计算特征向量。
的零空间计算特征向量。
在求解特征值时,有两个定理可以简化计算:
1) ,矩阵A的特征值之和等于矩阵A的迹;
,矩阵A的特征值之和等于矩阵A的迹;
2) ,矩阵A的特征值之积等于矩阵A的行列式值;
,矩阵A的特征值之积等于矩阵A的行列式值;
以 2 * 2 矩阵为例,给出以上结论的大致解释:
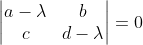 ,
,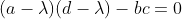 ,
,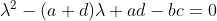 ,
,
由于  ,上式改写为
,上式改写为 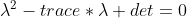 ,
,
解得  ,
,  ,
,
故 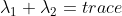 ,
,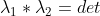 。
。
在求解  时,可能出现特征值
时,可能出现特征值  重复情况,这可能导致特征向量 x 不足,这样后面的分析也无法继续。特征值重复并不一定导致特征向量不足,如单位矩阵I,虽然其特征值都为1,但有n个不同的特征向量。
重复情况,这可能导致特征向量 x 不足,这样后面的分析也无法继续。特征值重复并不一定导致特征向量不足,如单位矩阵I,虽然其特征值都为1,但有n个不同的特征向量。
针对各个元素均为实数2*2情况,其特征值可能出现负数,如矩阵 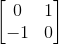 特征值为 i 和 -i。通过观察,如果矩阵A为对称矩阵,其特征值为实数;如果矩阵A为反对称矩阵,其特征值为一对共轭虚数。
特征值为 i 和 -i。通过观察,如果矩阵A为对称矩阵,其特征值为实数;如果矩阵A为反对称矩阵,其特征值为一对共轭虚数。
也就是说矩阵越接近对称矩阵,其特征值越有可能为实数。
二 矩阵对角化
假设矩阵A为n*n方阵,矩阵A有n个线性独立的特征向量  ,构成特征向量矩阵
,构成特征向量矩阵 ,其对应的特征值为
,其对应的特征值为 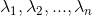 ,构成特征值矩阵
,构成特征值矩阵 ,则矩阵A可被对角化分解,其公式为:
,则矩阵A可被对角化分解,其公式为: ,推导如下:
,推导如下:
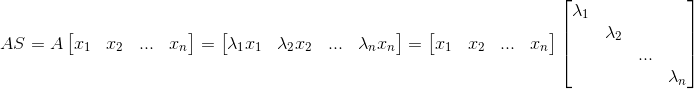 ,
, 。
。
如果已知 ,则有
,则有 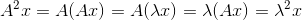 ,这表明矩阵
,这表明矩阵  的特征值为矩阵A的对应特征值的平方,矩阵
的特征值为矩阵A的对应特征值的平方,矩阵  与矩阵A有相同的特征向量。以上推导也可以通过矩阵对角化公式得到:
与矩阵A有相同的特征向量。以上推导也可以通过矩阵对角化公式得到: 。
。
针对A的任意整数次幂,可对角化为: ,这就提供了一个计算
,这就提供了一个计算 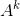 的方法。
的方法。
如果矩阵A可逆,则有: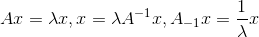 ,其逆矩阵与原矩阵有相同的特征向量和互为倒数的特征值。
,其逆矩阵与原矩阵有相同的特征向量和互为倒数的特征值。
三 应用(差分方程与微分方程)
1 复利
假设银行年利率为 .06,投资 1000 元后 5 年的收益为多少?
建立差分方程 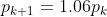 ,为了与后面的微分方程相比较,可将其改写为
,为了与后面的微分方程相比较,可将其改写为 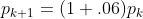 ,
,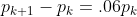 ,
,
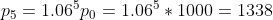 ;
;
如果按月计算复利,则有 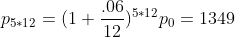 ;
;
如果按天计算复利,则有 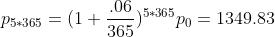 ;
;
如果按无限小时间计算复利,则有 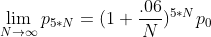 ,
,
由于 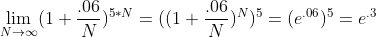 ,
,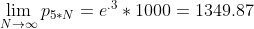 ;
;
可将差分方程 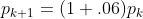 改写为无限小距离间的差分为
改写为无限小距离间的差分为  ,
,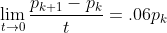 ,
,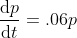 ;
;
以上 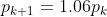 ,
,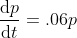 分别为复利的差分与微分方程。
分别为复利的差分与微分方程。
2 Fibonacci序列
Fibonacci定义为: ,该表达式为二阶差分,可通过一些技巧变换为一阶差分:
,该表达式为二阶差分,可通过一些技巧变换为一阶差分: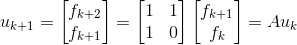 ,
,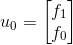 。
。
已知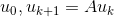 ,可推导出
,可推导出  。如果矩阵A可对角化,对
。如果矩阵A可对角化,对 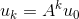 可做如下变换:
可做如下变换:
 ,将
,将 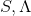 详细代入,则有
详细代入,则有 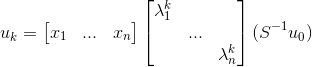 ,令
,令 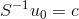 ,则
,则 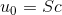 ,表明
,表明  由特征向量S按系数向量c线性组合得到。
由特征向量S按系数向量c线性组合得到。
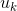 最终可被表示为:
最终可被表示为: 。
。
通过以上推导,如果仅需要计算某个特定的 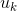 值,仅需使用公式
值,仅需使用公式  即可。使用
即可。使用 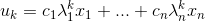 线性组合关系,可以通过特征值取值范围判断k趋近无穷大时其收敛状态;当所有特征值均满足
线性组合关系,可以通过特征值取值范围判断k趋近无穷大时其收敛状态;当所有特征值均满足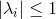 ,
,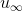 趋近稳定状态,可表示为:
趋近稳定状态,可表示为: (假设
(假设 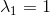 )或者
)或者 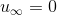 (假设所有特征值绝对值都小于1)。
(假设所有特征值绝对值都小于1)。
针对矩阵 ,计算特征值为
,计算特征值为  ,
, ,特征向量为
,特征向量为  ,
,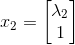 。根据以上分析,当k逐渐变大时,有:
。根据以上分析,当k逐渐变大时,有: 。
。
3 Markov矩阵
Markov矩阵定义如下:
1)矩阵所有元素均满足  ;
;
2)矩阵每列元素和等于1;
Markov矩阵具有如下性质:
1)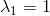 为Markov矩阵的一个特征值;
为Markov矩阵的一个特征值;
2)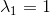 对应的特征向量
对应的特征向量  各个元素都为非负值;
各个元素都为非负值;
3)其他特征值满足 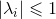 ;
;
4)Markov矩阵的幂级数稳定状态为: 。
。
给出一个具体的Markov矩阵  ,假设
,假设  是该矩阵的一个特征值,则有
是该矩阵的一个特征值,则有 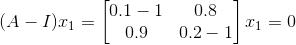 ,观察矩阵
,观察矩阵 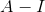 为奇异矩阵,
为奇异矩阵, 处于矩阵
处于矩阵 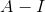 的零空间,则证明
的零空间,则证明  为Markov矩阵的一个特征值。
为Markov矩阵的一个特征值。
4 微分方程
标量常微分方程: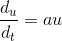 ,求解如下:
,求解如下:
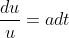 ,
, ,
, ,
,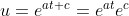 ;
;
已知 u(0),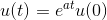 。
。
对于矢量常微分方程  ,已知 u(0),其解为
,已知 u(0),其解为 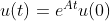 ,其中 A 为 n * n 矩阵,u(t),u(0) 为 n * 1 向量;
,其中 A 为 n * n 矩阵,u(t),u(0) 为 n * 1 向量;
这里需要关注 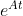 的含义:
的含义:
对于实数 a, 有 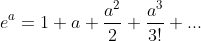 ,
,
对于矩阵 A,有  ,
,
带入 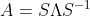 得
得  ,
,
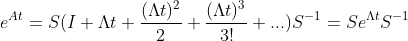 ,以 2 * 2 矩阵为例,
,以 2 * 2 矩阵为例,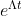 可分解为:
可分解为:
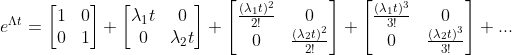 ,将各个矩阵相加得:
,将各个矩阵相加得:
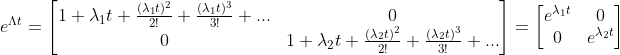 ,
,
将 u(0) 分解为特征向量得线性组合  ,
,
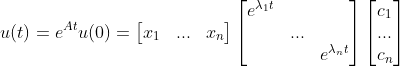 ,
,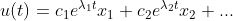 ,
,
以上推导出常微分方程的解,其解为每个特征向量的线性组合,与差分方程解  类似。
类似。
矢量常微分方程: ,矩阵A特征值与特征向量为:
,矩阵A特征值与特征向量为: ;
;
类比标量常微分方程,其解表达为:  ,将解整理:
,将解整理:
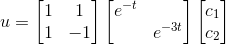 ,
, ,
, ,
, ,
, 。
。
观察以上微分方程解,当所有特征值均满足  ,u(t)收敛;当
,u(t)收敛;当 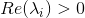 ,u(t)发散。
,u(t)发散。
参考资料:Linear Algebra And Its Applicaions Gilbert Strang



