[摘记]数值方法08——函数的极值
注:以下来自《C++数值算法一书》,仅对章节内容做摘要,为的是给自己扫盲,不涉及算法。
给定一个函数f,它依赖于一个或多个独立变量,求f达到某一极大值或极小值时自变量的取值,并计算出在这个极大值点或极小值点处函数f的取值。函数的极值可以是整体也可以是局部,一般求整体极值是一个很难解决的问题。本章标题也可称为最优化。
1. 一维黄金分割
二分法的思想完全可以平移到求极小值问题上,对于a<b<c,若f(b)比f(a)和f(c)都要小,则函数的极小值显然落在区间(a,c)内,最佳划界区间(a,b,c)应满足内点b与其中一个外点(如a)的距离比例为0.38197,而与另一个外点(如b)的距离比例为0.61803。
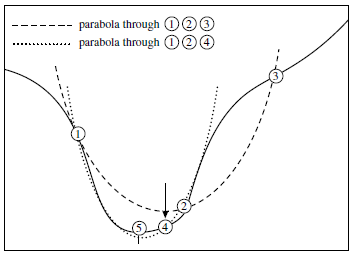
2. 抛物线内插和一维Brent方法
黄金分割方法用来处理最坏情况,而对于函数在极小值附近具有很好的抛物线性质,利用过任意三点拟合出来的抛物线,则能够很容易求出极小值,或者说非常接近极小值。这种方法称为逆抛物线内插。
Brent方法能够在目标函数允许的情况下,使用逆抛物线内插的方法求解,在函数不配合是依赖于一种收敛慢但可靠的算法。它通过记录6个函数点来完成以上任务。
3. 使用一阶导数的一维搜索方法
思想:根据在三个划界(a,b,c)之中心点的导数符号唯一地确定下一个试验点是取在(a,b)内,还是在(b,c)内。
4. 多维下降单纯形法
这个算法的效率并不是很高,但对于一个计算量小的问题,并且函数图形“可使计算速度变快些”,这时下降单纯法常常是最佳的方法。在多维情形下,我们所能做的就是给出一个初始预测值,即由自变量组成的一个N维向量作为迭代起点,然后设计一种算法不断进行下降搜索,直到找到极小值。单纯形法定义了五种收缩方法,用于搜索。
5. 多维情况下的方向集(Powell)方法
首先介绍一个子算法linmin:给定输入参数向量P和n以及函数f,求出使f(P+λn)达到最小的标量λ,然后以P+λn替代P,用λn替代n,结束。
接下来的几个方法都将基于这种逐步一维的方法,如果目标函数的梯度不能计算,则直观的方法是取一系列方向集合,
交替地沿这些一维方向搜索下去。
6. 多维共轭梯度法
思想:每次构造一个与原梯度方向共轭的方向,并且该方向还要尽可能地与在此之前所有已经过的方向共轭。
7. 多维变尺度法
变尺度法有时也称为拟牛顿法,目标是从逐步的线性极小化中不断累积信息,使得算法在经过N次线性极小化后,可以精确地收敛于一个N元二次型的极小值。变尺度法主要分为两大类,一类是Davidon-Fletcher-Powell(DFP)算法,另一类是Broyden-Fletcher-Goldfarb-Shanno(BFGS)算法。两种算法的不同之处仅仅在于舍入误差、收敛容差限以及一些类似的细节问题上。
8. 线性规划和单纯形法
线性规划的思想高中时就已经学过了,我这里就不赘述了。单纯形法的基本思想是对线性规划问题进行一系列的基本可行解的变换,在每次变换中,将右端变量与左端变量互调位置,而每一步都保持问题与原有问题完全等价。
9. 模拟退火法
这是一种适合于求解大规模优化问题的技术,特别是当优化问题有很多局部极值而全局极值又很难求出的时候。算法模拟自然界缓慢冷却的系统,采用一种截然不同的极小化算法,即所谓的Boltzmann概率分布。
本文原创,转载请注明出处