算法基础
介绍:
什么是算法?
算法(Algorithm):解决问题的精确步骤。

复习:递归
递归的两个特点:
- 调用自身
- 结束条件
看下面几个函数,哪个是递归,区别是什么:
def func1(x):
print(x)
func1(x-1)
def func2(x):
if x>0:
print(x)
func2(x+1)
def func3(x):
if x>0:
print(x)
func3(x-1)
def func4(x):
if x>0:
func4(x-1)
print(x)
# func3和func4是递归
func3 是先打印再递归,func4是先递归再打印。
print(func3(3)) 输出:3 2 1 None
print(func4(3)) 输出:1 2 3 None
递归,练习:


def func(depth): if depth == 0: print("我的小鲤鱼", end="") else: print("抱着", end="") func(depth - 1) print("的我", end="") func(3)
有序区:有的地方的数据已经完全变得有顺序,我们把这部分区域的数据成为有序区
无序区:有的地方的数据依旧无序,我们把这部分数据成为无序区
时间复杂度和空间复杂度:
时间复杂度是用来估计算法运行时间的一个式子(单位)。
一般来说,时间复杂度高的算法比复杂度低的算法慢。
常见的时间复杂度(按效率排序)
O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n2logn)<O(n3)
不常见的时间复杂度(看看就好)
O(n!) O(2n) O(nn) …
时间复杂度: 类比生活中的一些时间,估计实现: 眨一下眼 一瞬间/几毫秒 口算“29+68” 几秒 烧一壶水 几分钟 睡一觉 几小时 完成一个项目 几天/几星期/几个月 飞船从地球飞出太阳系 几年
如何一眼判断时间复杂度?
- 循环减半的过程 O(logn)
- 几次循环就是n的几次方的复杂度


空间复杂度:是用来评估算法内存占用大小的一个式子。
生产环境中,一般只考虑时间复杂度,很少考虑空间复杂度。
“空间换时间”,增加空间复杂度,能减少时间复杂度。
注:普通电脑计算能力是10的7次方到8次方之间。
一、冒泡排序
冒泡排序思路:
首先,列表每两个相邻的数,如果前边的比后边的大,那么交换这两个数...
代码关键点:
- 趟
- 无序区
注:趟表示从头到尾走一遍,趟是从0趟开始得。
总结:
- 优化,如果冒泡排序中执行一趟而没有交换,则列表已经是有序状态,可以直接结束算法。
- 冒泡时间复杂度:O(n^2)
- 最好情况复杂度 O(n)
- 平均情况复杂度 O(n^2)
- 最坏情况复杂度 O(n^2)
import random as rd import time import copy import sys def cal_time(func): def wrapper(*args, **kwargs): t1 = time.time() x = func(*args, **kwargs) t2 = time.time() print("%s running time %s secs." % (func.__name__, t2 - t1)) return x return wrapper @cal_time def bubble_sort(li): for i in range(len(li) -1): for j in range(len(li) -i -1): if li[j] > li[j+1]: li[j], li[j+1] = li[j+1], li[j] return li @cal_time def sys_sort(li): li.sort() return li li = list(range(10000)) rd.shuffle(li) print(li) li1 = copy.deepcopy(li) li2 = copy.deepcopy(li) li3 = copy.deepcopy(li) bubble_sort(li1) sys_sort(li2)
执行结果:
dubble_sort running time 0.013000726699829102 secs. sys_sort running time 0.008000373840332031 secs.
优化代码:
def bubble_sort(li):
for i in range(len(li) -1):
exchange = False
for j in range(len(li) -i -1):
if li[j] > li[j+1]:
li[j], li[j+1] = li[j+1], li[j]
exchange = True
if not exchange:
break
return li
二、选择排序
选择排序思路:
一趟遍历记录最小的数,放到第一个位置;
再一趟遍历记录剩余列表中最小的数,继续放置;
……
三、插入排序
列表被分为有序区和无序区两个部分。最初有序区只有一个元素。
每次从无序区选择一个元素,插入到有序区的位置,直到无序区变空。
四、快排
快速排序突出一个字快,是好写的排序算法里最快的,快的排序算法里最好写得。
快排算法关键点:
- 归位
- 递归
快排思路:
- 取一个元素P(第一个元素),使元素p归位。
- 列表被p分成两部分,左边都比p小,右边都比p大。
- 递归完成排序。
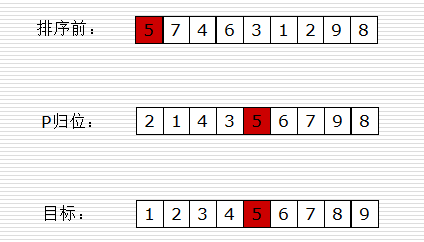
总结,问题:
- 最坏情况,复杂度增加 O(n^2)
- 递归(递归限制)

import random as rd import time import sys import copy 设置递归限制 sys.setrecursionlimit(100000) def cal_time(func): def wrapper(*args,**kwargs): t1 = time.time() x = func(*args,**kwargs) t2 = time.time() print("%s running time %s secs." % (func.__name__, t2 - t1)) return x return wrapper @cal_time def sys_sort(li): li.sort() return li def _quick_sort(data, left, right): if left < right: mid = partition(data, left, right) _quick_sort(data, left, mid-1) _quick_sort(data, mid + 1, right) def partition(data, left, right): tmp = data[left] while left < right: while left < right and data[right]>=tmp: right-=1 data[left]=data[right] while left < right and data[left]<=tmp: left+=1 data[right]=data[left] data[left]=tmp return left @cal_time def quick_sort(data): return _quick_sort(data, 0, len(data)-1) li = list(range(100000)) rd.shuffle(li) li1 = copy.deepcopy(li) li2 = copy.deepcopy(li) quick_sort(li1) sys_sort(li2)
五、希尔排序
希尔排序思路:

注:希尔排序每趟并不使某些元素有序,而是使整体数据越来越接近有序;最后一趟排序使得所有数据有序。
时间复杂度:
O((1+τ)n) ,τ表示在0到1之间 O(1.3n)
代码实现:
def insert_sort_gap(li, gap): for i in range(gap, len(li)): tmp = li[i] j = i - gap while j >= 0 and tmp < li[j]: li[j + gap] = li[j] j = j - gap li[j + gap] = tmp def shell_sort(li): d = len(li) // 2 while d > 0: insert_sort_gap(li, d) d = d //2 return li li=[3,4,5,1,2,9,8,11] print(shell_sort(li))
优化代码:
def shell_sort(li):
gap = len(li) // 2
while gap > 0:
for i in range(gap, len(li)):
tmp = li[i]
j = i - gap
while j >=0 and tmp < li[j]:
li[j + gap] = li[j]
j -= gap
li[j + gap] = tmp
gap = gap // 2
return li
li=[3,4,5,1,2,9,8,11]
print(shell_sort(li))
排序小结:
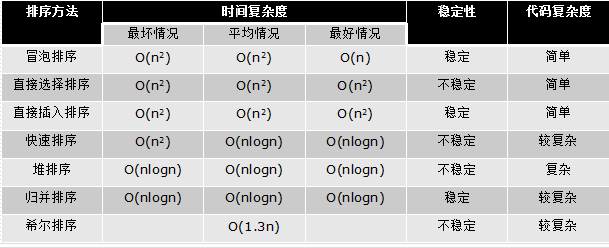




 浙公网安备 33010602011771号
浙公网安备 33010602011771号