python基础之递归、二分法

 一 递归

1. 必须有一个明确的结束条件
2. 每次进入更深一层递归时，问题规模相比上次递归都应有所减少
3. 递归效率不高，递归层次过多会导致栈溢出（在计算机中，
函数调用是通过栈（stack）这种数据结构实现的，每当进入一个函数调用，
栈就会加一层栈帧，每当函数返回，栈就会减一层栈帧。由于栈的大小不是无限的，
所以，递归调用的次数过多，会导致栈溢出）

注：栈遵循先进后出，先吃后拉原则。

　　递归能干得事，while True都能干。

查看和修改栈的大小：

>>> import sys
>>> sys.getrecursionlimit()
1000
>>>
>>> sys.setrecursionlimit(10000)
>>> sys.getrecursionlimit()
10000
>>>

 递归初识：

part1:

def test():
    test()
test()

输出结果：

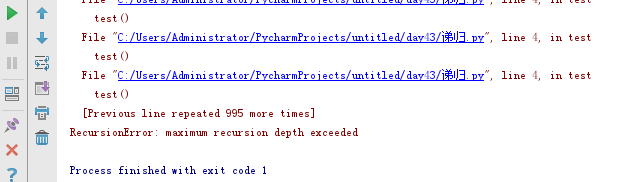
#part2:

#：有一个明确的结束条件
def test(n):
    print(n)
    n = n -1
    if n >=1:
        test(n)
test(5)

输出结果：

#part3

def calc(n):
    print(n)
    if int(n/2)==0:
        return n
    return calc(int(n/2))
print('********',calc(10))

输出结果：

 

#part4

# 5 = 5*4*3*2*1（实现阶乘）

def func(num):
    if num==1:
        return 1
    if num>1:
        return func(num-1)*num
k = func(5)  
print(k)

输出结果：

分析过程：

"""
def func(num):
    if num==1:
        return 1
    if num>1:
        return func(num-1)*num
k = func(5)  
print(k)                   #最后k等于120

def func(5):
    if 5==1:
        return 1
    if 5>1:
        return func(4)*5   #返回时func(4) 等于 24 , func(4)*5

def func(4):
    if 4==1:
        return 1
    if 4>1:
        return func(3)*4   #返回时func(3) 等于 6 , func(3)*4 等于 24

def func(3):
    if 3==1:
        return 1
    if 3>1:
        return func(2)*3   #返回时func(2) 等于 2 , func(2)*3 等于 6

def func(2):
    if 2==1:
        return 1
    if 2>1:
        return func(1)*2   #返回时func(1) 等于 1 , func(1)*2 等于 2

def func(1): 
    if 1==1:
        return 1           #最终得出结论func(1) 等于 1，开始返回
"""

 

使用实例：

猜年龄游戏：

小白问小黄年龄多少，小黄说比小蓝大两岁。又问小蓝年龄多少，小蓝说比小红大两岁。

又问小红年龄多少，小红说比小绿大两岁。又问小绿年龄多少，小绿说比小青大两岁。、

又问小青多大，小青说10岁了。问小黄现在多大？

 

分析：

 

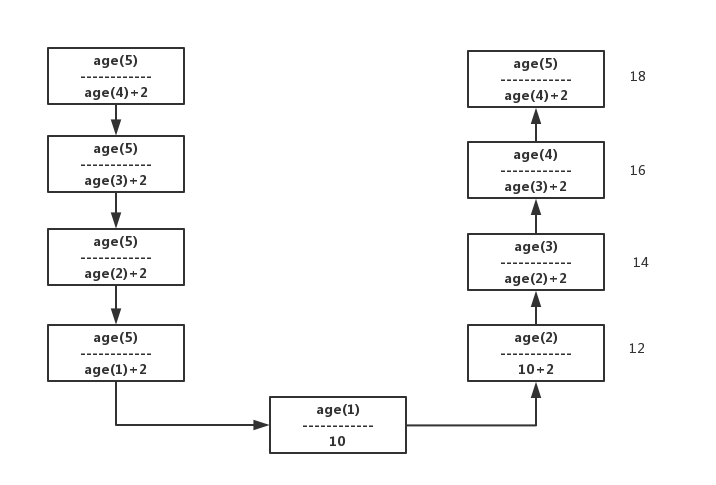
age(5)=age(4)+2　　 n=5 age(n)=age(n-1)+2
age(4)=age(3)+2 　　n=4 age(n)=age(n-1)+2
age(3)=age(2)+2 　　n=3 age(n)=age(n-1)+2
age(2)=age(1)+2 　　n=2 age(n)=age(n-1)+2
age(1)=10 　　　　　 n=1 age(n)=10

n=1 res=10
n>1 res=age(n-1)+2

答案：

def age(n):
    if n == 1:
        return 10
    else:
        return age(n-1)+2

print(age(5))

 

二 二分法

猜数字是否在列表内游戏：

# data=[]
# for i in range(1,100000,2):
#    data.append(i)


data = [1, 3, 6, 7, 9, 12, 14, 16, 17, 18, 20, 21, 22, 23, 30, 32, 33, 35]
# num=19
# i=0
# while True:
#     if num == data[i]:
#         print('find it')
#         break
#     i+=1

def search(num,data):
    print(data)
    if len(data) > 1:
        #二分
        mid_index=int(len(data)/2)
        mid_value=data[mid_index]
        if num > mid_value: #19>18
            #num在列表的右边
            data=data[mid_index:] #data[0:]-->[18]
            search(num,data)
        elif num < mid_value:
            #num在列表的左边
            data=data[:mid_index]
            search(num,data)
        else:
            print('find it')
            return
    else:
        if data[0] == num:
            print('find it')
        else:
            print('not exists')

# search(9527,data)
search(15,data)
# search(1,data)