数据结构基础

什么是数据结构？

简单来说，数据结构就是设计数据以何种方式组织并存储在计算机中。

比如：列表、集合与字典等都是一种数据结构。

N.Wirth: “程序=数据结构+算法”

 

列表：

在其他编程语言中称为“数组”，是一种基本的数据结构类型。

列表是一种线性表，是固定长度的。

一个整数，在32位机器中，占用4个字节，在64位机器中，占用8个字节。

列表在内存中开得格子要一样大：

1. 第一是为了存地址，地址是一样大得。64位机器是一个格子占用8个字节。
2. 第二是为了查找，如li[2] 在64位机器中等于li+2*8

列表和数组有两种不同：

1. 元素类型不同
2. 可以无限append。如果格子空间不够，再开一个以前两倍的空间

关于列表的问题：

1. 列表中元素是如何存储的？

   是连续存储得，地址在内存中是连续得。

2. 列表提供了哪些基本的操作？

   append、pop、remove、insert、index、直接通过下标查找。

3. 这些操作的时间复杂度是多少？

   按下标查询，复杂度O(1)
   插入(insert)，复杂度O(n)
   删除(remove)，复杂度O(n) , pop()是O(1), pop(-2)是O(n)
   添加(append), 复杂度O(1)
   查找(index),复杂度O(n)

栈：

栈(Stack)是一个数据集合，可以理解为只能在一端进行插入或删除操作的列表。

栈的特点：后进先出（last-in, first-out）

栈的概念：栈顶、栈底

栈的基本操作：

1. 进栈（压栈）：push
2. 出栈：pop
3. 取栈顶：gettop

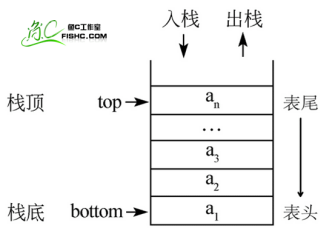
栈的Python实现

不需要自己定义，使用列表结构即可。

1. 进栈函数：append
2. 出栈函数：pop
3. 查看栈顶函数：li[-1]

栈的应用：

一、word操作：

Ctrl + C 之后，会先从撤销栈pop删除，append重做栈
Ctr + Y 之后，会把重做栈中pop删除，append撤销栈。
只加值得时候，只有撤销栈。

 二、括号匹配问题

括号匹配问题：给一个字符串，其中包含小括号、中括号、大括号，求该字符串中的括号是否匹配。

例如：

• ()()[]{} 匹配
• ([{()}]) 匹配
• []( 不匹配
• [(]) 不匹配

代码实现：

def check_kuohao(s):
    stack = []
    for char in s:
        if char in {'(','[','{'}:
            stack.append(char)
        elif char == ')':
            if len(stack) > 0 and stack[-1] == '(':
                stack.pop()
            else:
                return False
        elif char == ']':
            if len(stack) > 0 and stack[-1] == '[':
                stack.pop()
            else:
                return False
        elif char == '}':
            if len(stack) > 0 and stack[-1] == '{':
                stack.pop()
            else:
                return False

    if len(stack) == 0:
        return True
    else:
        return False

s="{[()]}"
print(check_kuohao(s))

三、迷宫问题

给一个二维列表，表示迷宫（0表示通道，1表示围墙）。给出算法，求一条走出迷宫的路径。

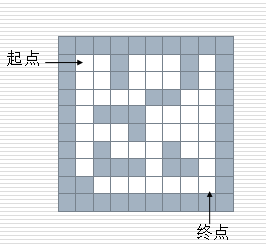
maze = [
    [1,1,1,1,1,1,1,1,1,1],
    [1,0,0,1,0,0,0,1,0,1],
    [1,0,0,1,0,0,0,1,0,1],
    [1,0,0,0,0,1,1,0,0,1],
    [1,0,1,1,1,0,0,0,0,1],
    [1,0,0,0,1,0,0,0,0,1],
    [1,0,1,0,0,0,1,0,0,1],
    [1,0,1,1,1,1,1,1,1,1],
    [1,1,0,0,0,0,0,0,0,1],
    [1,1,1,1,1,1,1,1,1,1]
]

解决思路：

在一个迷宫节点(x,y)上，可以进行四个方向的探查：maze[x-1][y], maze[x+1][y], maze[x][y-1], maze[x][y+1]
思路：从一个节点开始，任意找下一个能走的点，当找不到能走的点时，退回上一个点寻找是否有其他方向的点。
方法：创建一个空栈，首先将入口位置进栈。当栈不空时循环：获取栈顶元素，寻找下一个可走的相邻方块，如果找不到可走的相邻方块，说明当前位置是死胡同，进行回溯（就是讲当前位置出栈，看前面的点是否还有别的出路）

代码实现：

maze = [
    [1,1,1,1,1,1,1,1,1,1],
    [1,0,0,1,0,0,0,1,0,1],
    [1,0,0,1,0,0,0,1,0,1],
    [1,0,0,0,0,1,1,0,0,1],
    [1,0,1,1,1,0,0,0,0,1],
    [1,0,0,0,1,0,0,0,0,1],
    [1,0,1,0,0,0,1,0,0,1],
    [1,0,1,1,1,1,1,1,1,1],
    [1,1,0,0,0,0,0,0,0,1],
    [1,1,1,1,1,1,1,1,1,1]
]

dirs = [
    lambda x,y:(x+1,y),
    lambda x,y:(x-1,y),
    lambda x,y:(x,y+1),
    lambda x,y:(x,y-1)
]

def mgmaze(x1,y1,x2,y2):
    stack=[]
    stack.append((x1,y1))
    while len(stack)>0: #只要栈不为空
        curNode = stack[-1]
        if curNode[0]==x2 and curNode[1]==y2:
            #到达终点 打印路径
            for p in stack:
                print(p)
            return True

        for dir in dirs:
            nextNode = dir(curNode[0],curNode[1])
            if maze[nextNode[0]][nextNode[1]] == 0:
                stack.append(nextNode)
                maze[nextNode[0]][nextNode[1]] = 2 #2表示已走过
                break
        else:
            stack.pop()
            maze[curNode[0]][curNode[1]] = 2 #死路一条
    return False

print(mgmaze(1,1,8,8))

 队列：

队列(Queue)是一个数据集合，仅允许在列表的一端进行插入，另一端进行删除。

进行插入的一端称为队尾(rear)，插入动作称为进队或入队。

进行删除的一端称为队头(front)，删除动作称为出队

队列的性质：先进先出(First-in, First-out)

 

双向队列：队列的两端都允许进行进队和出队操作。

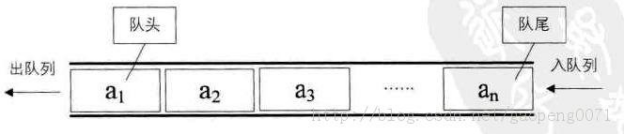
队列能否简单用列表实现？为什么？

不能

使用方法：from collections import deque

1. 创建队列：queue = deque(li)
2. 进队：append
3. 出队：popleft
4. 双向队列队首进队：appendleft
5. 双向队列队尾进队：pop

队列的实现原理：

1. 初步设想：列表+两个下标指针
2. 创建一个列表和两个变量，front变量指向队首，rear变量指向队尾。初始时，front和rear都为0。
3. 进队操作：元素写到li[rear]的位置，rear自增1。
4. 出队操作：返回li[front]的元素，front自减1。

这种实现的问题？

 

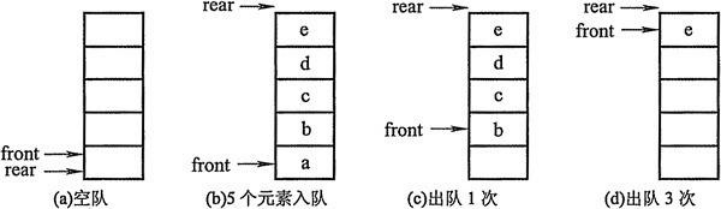
队列的实现原理——环形队列

改进方案：将列表首尾逻辑上连接起来。

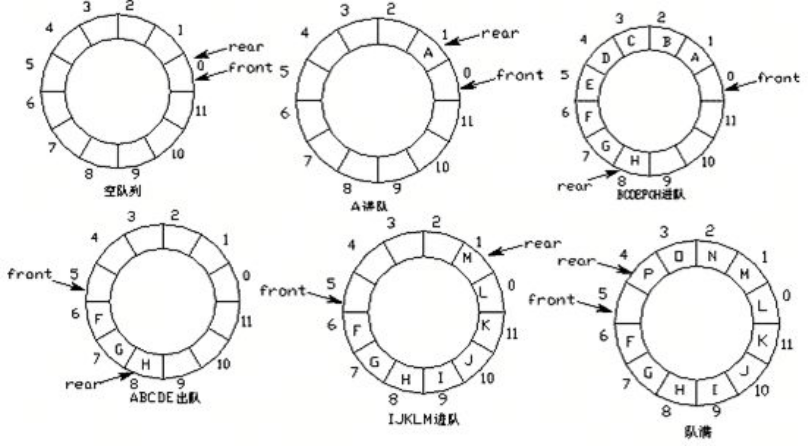
环形队列：当队尾指针front == Maxsize + 1时，再前进一个位置就自动到0。

1. 实现方式：求余数运算
2. 队首指针前进1：front = (front + 1) % MaxSize
3. 队尾指针前进1：rear = (rear + 1) % MaxSize
4. 队空条件：rear == front
5. 队满条件：(rear + 1) % MaxSize == front

队列的应用——迷宫问题

思路：从一个节点开始，寻找所有下面能继续走的点。继续寻找，直到找到出口。
方法：创建一个空队列，将起点位置进队。在队列不为空时循环：出队一次。如果当前位置为出口，则结束算法；否则找出当前方块的4个相邻方块中可走的方块，全部进队。

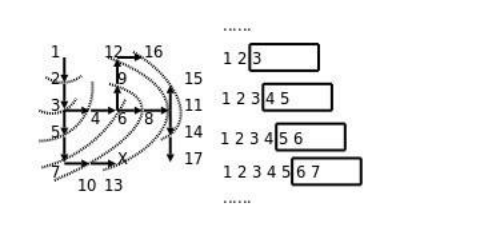
代码实现：

from collections import deque

maze = [
    [1,1,1,1,1,1,1,1,1,1],
    [1,0,0,1,0,0,0,1,0,1],
    [1,0,0,1,0,0,0,1,0,1],
    [1,0,0,0,0,1,1,0,0,1],
    [1,0,1,1,1,0,0,0,0,1],
    [1,0,0,0,1,0,0,0,0,1],
    [1,0,1,0,0,0,1,0,0,1],
    [1,0,1,1,1,1,1,1,1,1],
    [1,1,0,0,0,0,0,0,0,1],
    [1,1,1,1,1,1,1,1,1,1]
]

dirs = [
    lambda x,y:(x+1,y),
    lambda x,y:(x-1,y),
    lambda x,y:(x,y+1),
    lambda x,y:(x,y-1)
]


def mgpath(x1, y1, x2, y2):
    queue = deque()
    path = []
    queue.append((x1, y1, -1))
    while len(queue) > 0:
        curNode = queue.popleft()
        path.append(curNode)
        if curNode[0] == x2 and curNode[1] == y2:
            #到达终点
            print(path)
            return True
        for dir in dirs:
            nextNode = dir(curNode[0], curNode[1])
            if maze[nextNode[0]][nextNode[1]] == 0: #找到下一个方块
                queue.append((*nextNode, len(path) - 1))
                maze[nextNode[0]][nextNode[1]] = -1 # 标记为已经走过
    return  False

链表：

链表中每一个元素都是一个对象，每个对象称为一个节点，包含有数据域key和指向下一个节点的指针next。通过各个节点之间的相互连接，最终串联成一个链表。

链表是和数组或者列表相对的概念，链表也是个线性数据结构。

链表和数组的区别是，它不是连续得。

python没有封装链表，所以要自己写。

二叉树按二维数组存，树是按照链表存。

链表的优缺点：

好处：链表的插入和删除比列表快，复杂度是O(1)
坏处：按照下标查找是O(n)，很慢

关键字：

• 数据域
• 指针域

节点定义：

class Node(object):
    def __init__(self, item):
        self.item = item
        self.next = None

头结点

class Node(object):
    def __init__(self, item):
        self.item = item
        self.next = None


n1 = Node(1)
n2 = Node(2)
n3 = Node(3)
n1.next = n2
n2.next = n3

print(n1.next.next.item)

class BinTreeNode:
    def __init__(self, item):
        self.item = item
        self.lchild = None
        self.rchild = None

n1 = BinTreeNode(1)
n2 = BinTreeNode(2)
n3 = BinTreeNode(3)
n4 = BinTreeNode(4)

n1.lchild = n2
n1.rchild = n3
n3.lchild = n4

遍历链表：

def traversal(head):
    curNode = head  # 临时用指针
    while curNode is not None:
        print(curNode.data)
        curNode = curNode.next

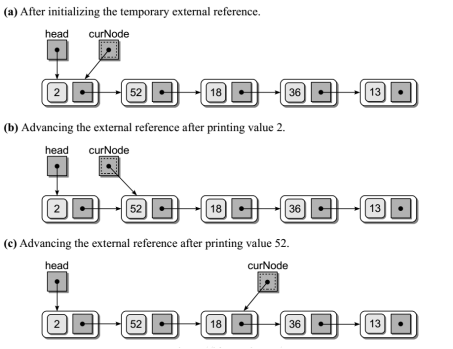
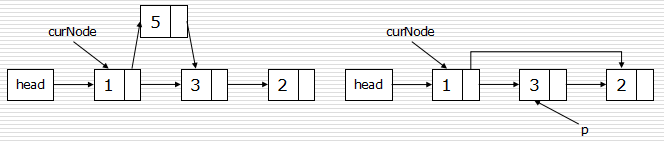
链表节点的插入和删除：顺序不能反

插入：

p.next = curNode.next
curNode.next = p

删除：

p = curNode.next
curNode.next = curNode.next.next
del p

建立链表

头插发和尾插法都是单链表，只能从前往后找。

1. 头插法：头插法建立得数据正好是相反得。

def createLinkListF(li):
    l = Node()
    for num in li:
        s = Node(num)
        s.next = l.next
        l.next = s
return l

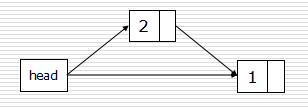
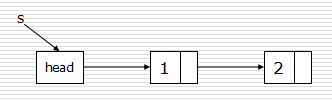
　　2.尾插法：

def createLinkListR(li):
    l = Node()
    r = l #r指向尾节点
    for num in li:
        s = Node(num)
        r.next = s
        r = s

双链表：

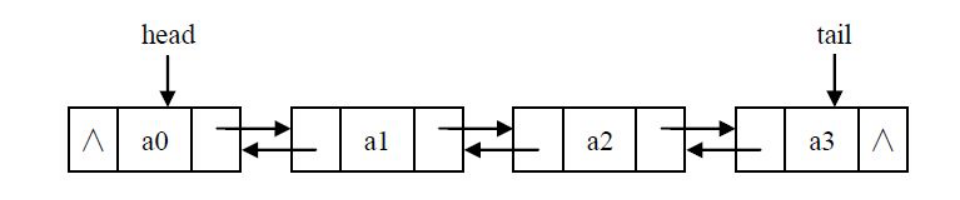
头插法和尾插法都是单链表，只能从前往后找。如果想从后往前找，就需要双链表。

双链表中每个节点有两个指针：一个指向后面节点、一个指向前面节点。

节点定义：

class Node(object):
    def __init__(self, item=None):
        self.item = item
        self.next = None
        self.prior = None

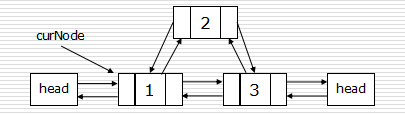
双链表节点的插入和删除：

插入：

p.next = curNode.next
curNode.next.prior = p
p.prior = curNode
curNode.next = p

删除：

p = curNode.next
curNode.next = p.next
p.next.prior = curNode
del p

建立双链表

尾插法：

def createLinkListR(li):
    l = Node()
    r = l
    for num in li:
        s = Node(num)
        r.next = s
        s.prior = r
        r = s
    return l, r

列表与链表复杂度：

按元素值查找:
    按顺序查找，复杂度是一样的。
    按二分查找，链表没法查找.
按下标查找:
    列表是O(1)
    链表是O(n)
在某元素后插入:
    列表是O(n)
    链表是O(1)
删除某元素:
    列表是O(n)
    链表是O(1)

集合与字典

集合是对值进行哈希，字典是对键进行哈希。它们两个进行查找得时候，就比列表快。

md5就是一种哈希算法。

集合与字典都是通过哈希表查找。

哈希表（Hash Table，又称为散列表），是一种线性表的存储结构。通过把每个对象的关键字k作为自变量，通过一个哈希函数h(k)，将k映射到下标h(k)处，并将该对象存储在这个位置。

例如：数据集合{1,6,7,9}，假设存在哈希函数h(x)使得h(1) = 0, h(6) = 2, h(7) = 4, h(9) = 5，那么这个哈希表被存储为[1,None, 6, None, 7, 9]。

当我们查找元素6所在的位置时，通过哈希函数h(x)获得该元素所在的下标（h(6) = 2），因此在2位置即可找到该元素。

哈希函数种类有很多，这里不做深入研究。

哈希冲突或者哈希碰撞：由于哈希表的下标范围是有限的，而元素关键字的值是接近无限的，因此可能会出现h(102) = 56， h(2003) = 56这种情况。此时，两个元素映射到同一个下标处，造成哈希冲突。

解决哈希冲突：

拉链法:将所有冲突的元素用链表连接
开放寻址法:通过哈希冲突函数得到新的地址

在Python中的字典：a = {'name': 'Alex', 'age': 18, 'gender': 'Man'}

使用哈希表存储字典，通过哈希函数将字典的键映射为下标。假设h(‘name’) = 3, h(‘age’) = 1, h(‘gender’) = 4，则哈希表存储为[None, 18, None, ’Alex’, ‘Man’]

在字典键值对数量不多的情况下，几乎不会发生哈希冲突，此时查找一个元素的时间复杂度为O(1)。

 

补充：

数据存储分为物理存储方式和逻辑存储方式。

数据的物理结构包括顺序存储的存储和链式存储的存储。

线性结构

数据结构的的逻辑结构分为线性结构和数据结构。线性结构是n个数据元素的有序（次序）集合。

线性结构是一个有序数据元素的集合，数据元素之间存在着“一对一”的线性关系的数据结构。通俗一点就是一个数据结构只有一个前置节点和一个后置节点得时候，就是线性数据结构。

非线性结构的逻辑特征是一个结点元素可能对应多个直接前驱和多个后继。通俗一点就是一个数据结构有多个前置节点和多个后置节点。

树形数据结构，就是由一个前置数据节点，多个后置节点。

图形数据结构，有多个前置节点和多个后置节点。

常用的线性结构有：线性表，栈，队列，双队列，数组，串。

常用的非线性结构有：二维数组，多维数组，广义表，树(二叉树)，图。

 

例子：

传统文本（例如书籍中的文章和计算机的文本文件）都是线性结构，阅读是需要注意顺序阅读，而超文本则是一个非线性结构。在制作文本时，可将写作素材按内部联系划分成不同关系的单元，然后用制作工具将其组成一个网型结构。阅读时，不必按线性方式顺序往下读，而是有选择的阅读自己感兴趣的部分。
在超文本文件中，可以用一些单词，短语或图像作为连接点。这些连接点通常同其他颜色显示或加下划线来区分，这些形式的文件就成为超文本文件。通过非线性结构，可能实现页面任意跳转。
有一个以上根结点的数据结构一定是非线性结构。