1.学习总结(2分)
这一章总体学的自我感觉还挺清晰明了的,并且图在实际情况中有很多的应用,很灵活也很有用,pta上的那些题目就可以反映出来。可是只是掌握了基本概念,代码方面的编写对我来说非常困难。所以做题时借鉴了很多网上资源。
1.1图的思维导图

1.2 图结构学习体会
谈谈你对图结构中的几个经典算法学习体会。具体有:
- 深度遍历算法:一条路走到黑,再从最后一个返回其相邻节点返回还未遍历的,在邻接矩阵中写出其深度遍历的顺序更快捷
- 广度遍历算法:一层一层地完全遍历。
- Prim算法:出发点是通过不断来比较路径权值选择路径更换起点。
- Kruscal算法:直接通过比较权值,选出最短的几条路经,然后再比较权值将其中顶点相连生成最小生成树
- Dijkstra算法:不断引入新的顶点,再计算引入新的顶点后是否会引起整体路径更短,整体处于变动之,但也更准确,确定是最短路径。
- 拓扑排序算法:虚删的操作很巧妙,值得借鉴。
2.PTA实验作业(4分)
本周要求挑选出3道题目书写设计思路、调试过程。设计思路使用伪代码描述。题目选做要求:
- 不能选6-1,6-2,6-3
具体书写内容及格式如下:
题目一:7-1 图着色问题:
1.设计思路(伪代码或流程图)
判断对于给定了v各点,e条边的无向图,看能不能用k种颜色给这个图进行染色,要求两个直接联通的定点不能用相同的颜色进行染色。
除了要判断是否连通的两点是不同的颜色外,还要判断总共的颜色的个数一定要等于k。
染色的个数可以在给每一个顶点赋予颜色的时候直接计算,至于是否两点的颜色一样,可以在每次输入的时候判断标号比他小的所有的直接联通的点两点间的颜色,(因为存的时候是无向图,正向和反向的两条边都存下来了)。
2. 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)
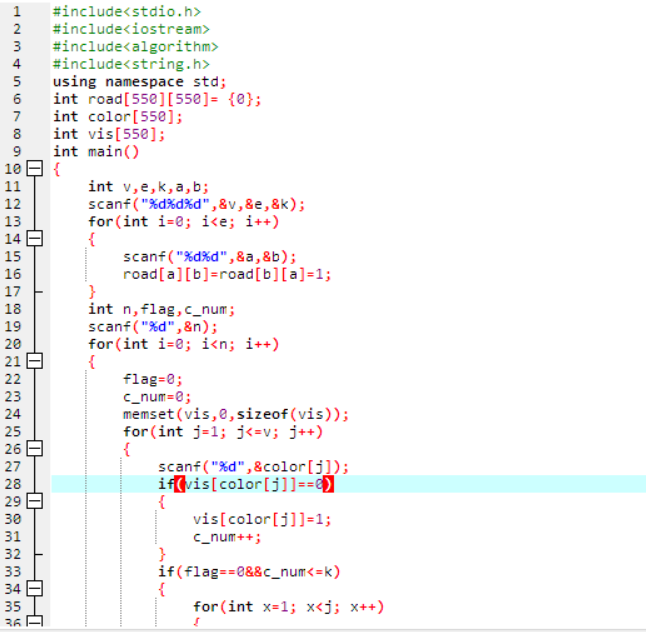
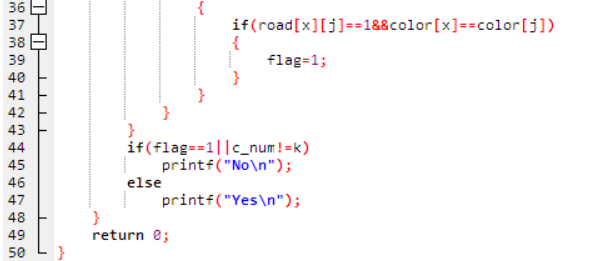
2.4 PTA提交列表说明。


1.忘记选择编译器环境
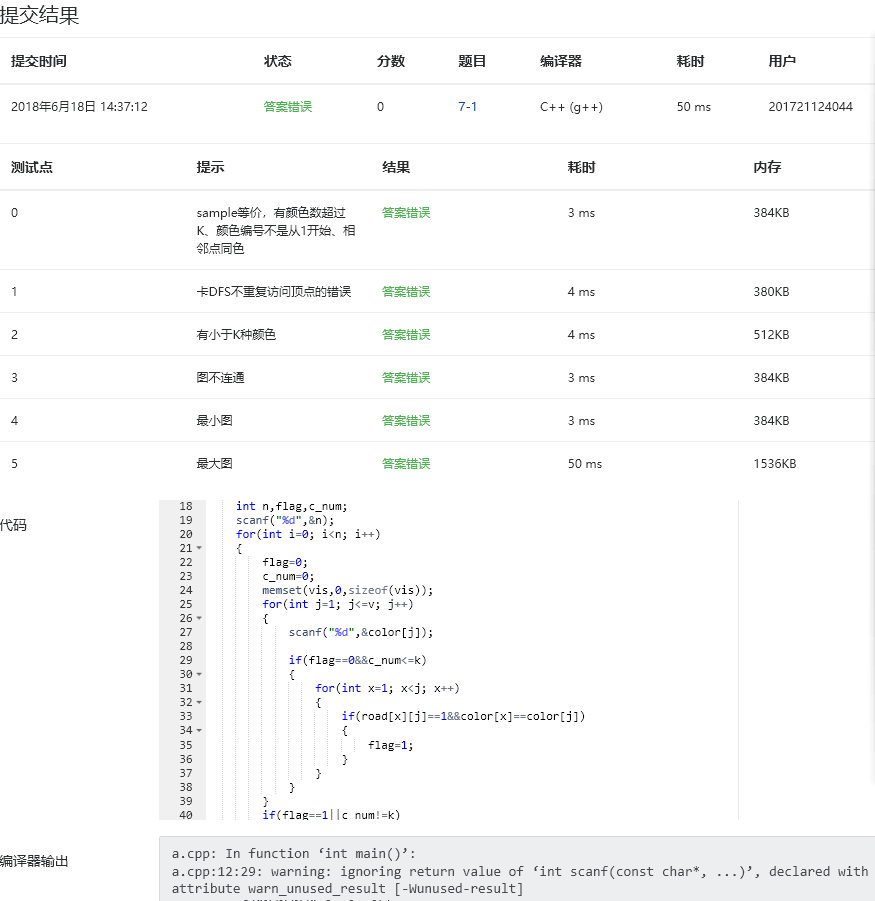
2.遗漏了当前这个点颜色没出现过的情况

重新选择编译器并且补全情况就好了。
题目二:7-7 旅游规划:
1.设计思路:这道题就是一道Dijastra算法题,存储时运用2个二维数组构建成邻接表来分别存储 两城市之间的距离和 需要的费用,注意点的就是 Dijastra算法 不仅需要判断 dist 还需要判断 acost
2.代码截图:
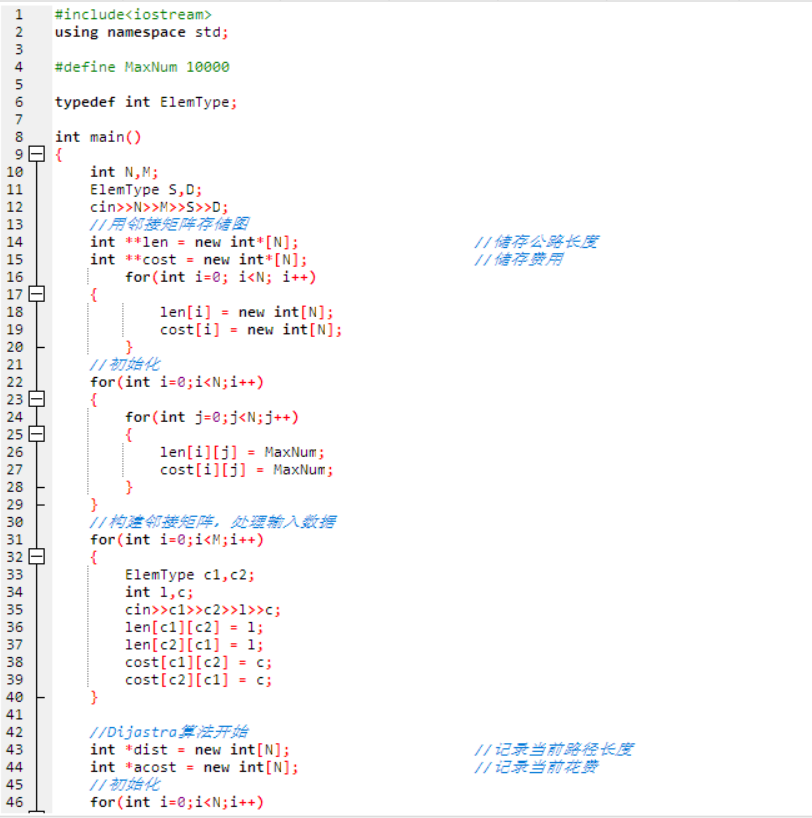
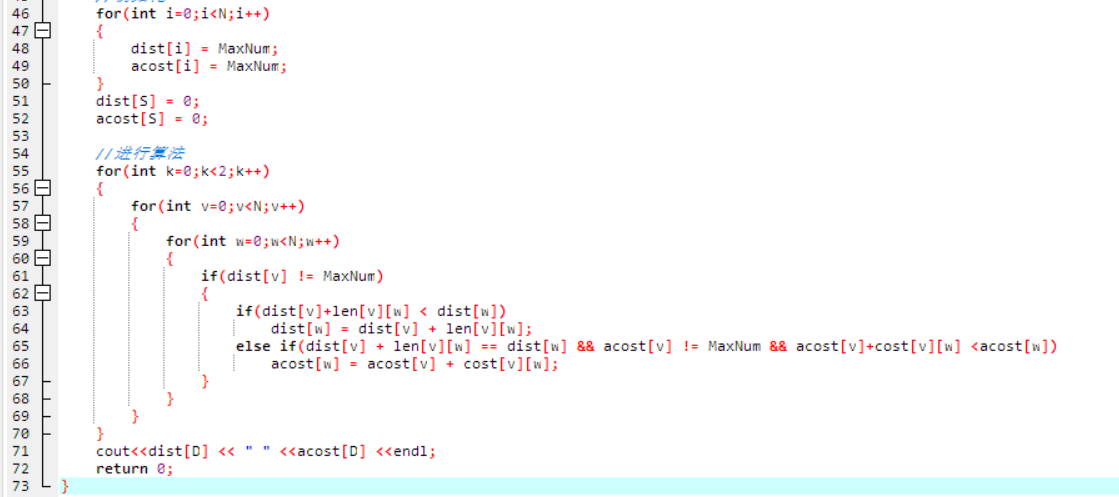
3.提交列表具体说明:

总的来说这题还是相对简单,用Dijkstra算法可以很好的解决。编译错误还是因为编译环境的问题。。在dev上也有好好运行测试过,所以后来就直接通过了。
题目三:7-8 城市间紧急救援
1.设计思路:
这是一道最短路基础上求最短路径长度和点权和最大值的问题,同时要记录最短路径.
运用迪杰斯特算法求出最短路,在做松弛时,由于要记录最短路径长度,所以当dis[i]=dis[j]+map[i][j]时,说明存在另外的路径让当前点到起点的距离最小,需要把pathnum[j](到达j点的最短路径长度,下同)加到pathnum[i]上.
用toval数组记录当前点满足最短路前提下的点权和的最大值,每次松弛操作都要更新,当dis[i]=dis[j]+map[i][j]时,判断total[j]+b[j](当前点的权值)是否大于total[i],如果大于就需要更新. 用pre数组作前缀数组,在每次松弛操作和dis[i]=dis[j]+map[i][j]相等时更新.
2.代码截图:
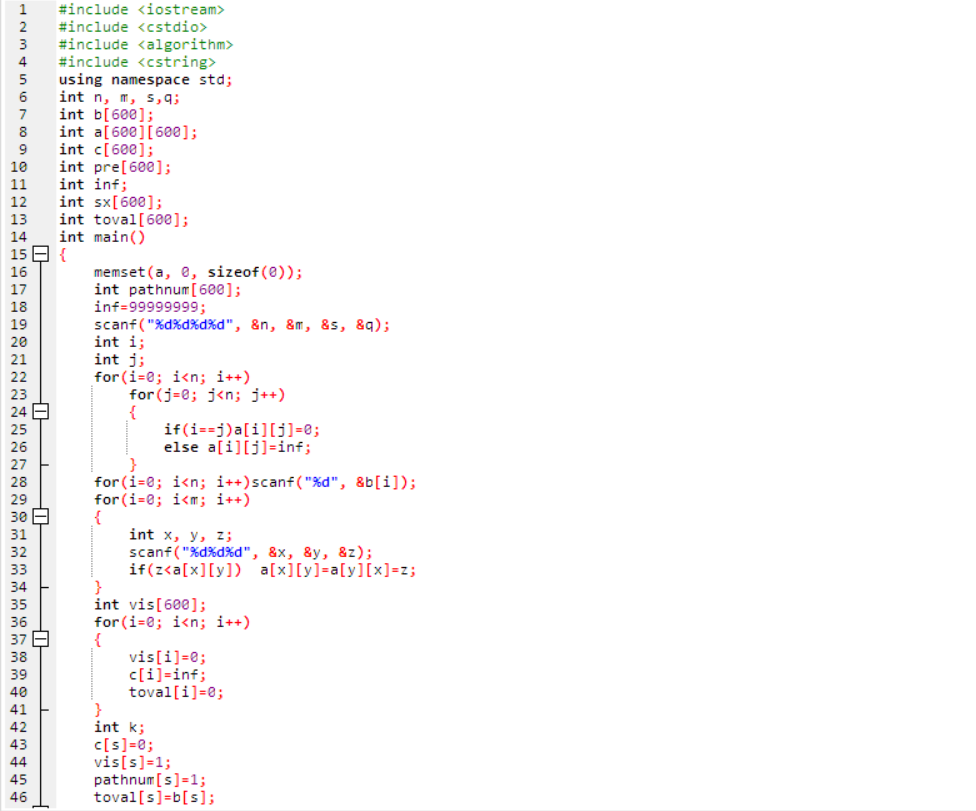
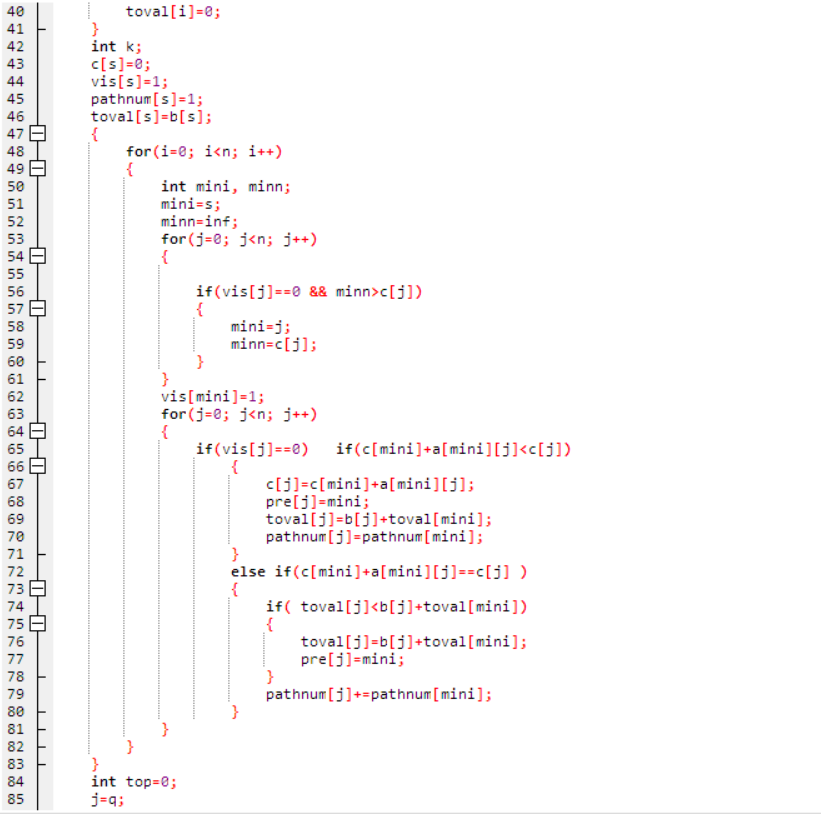
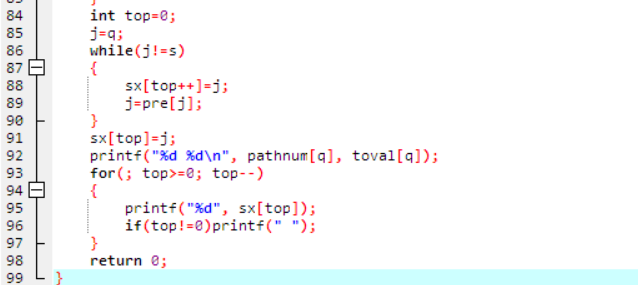
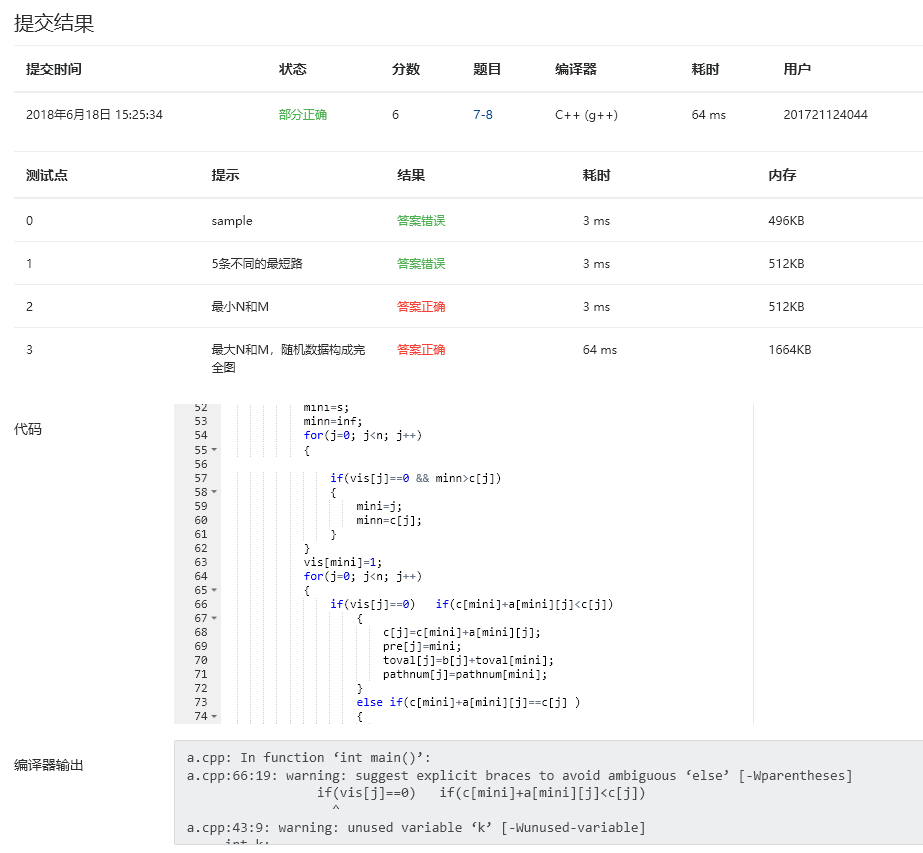
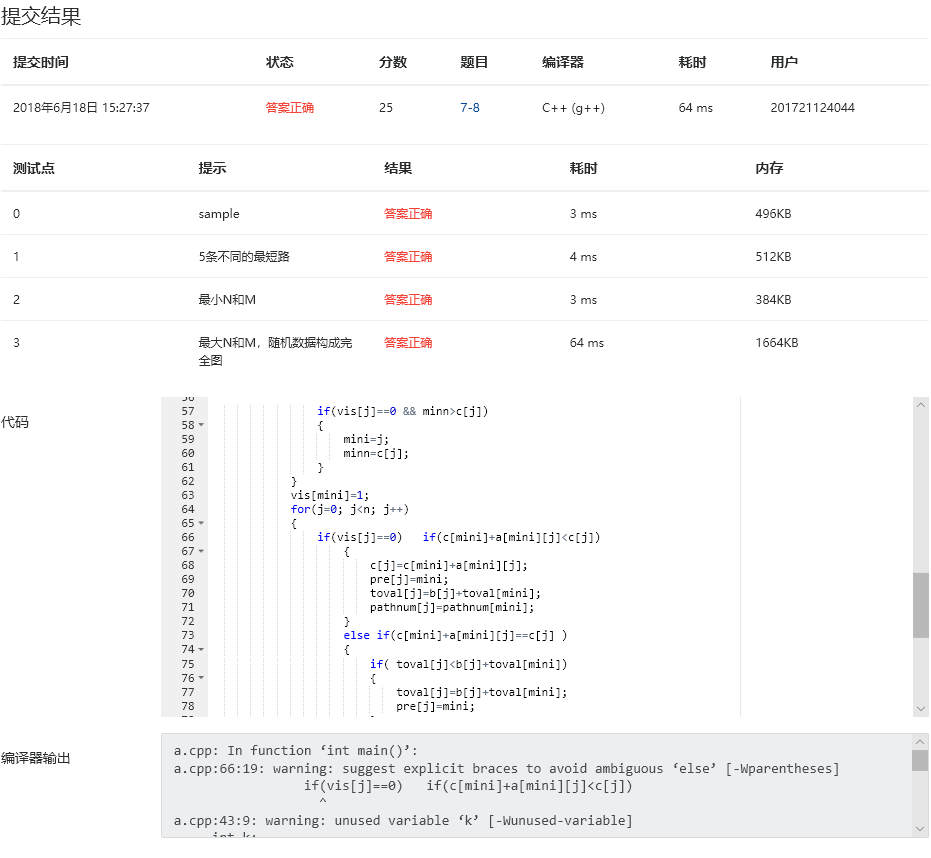
3.提交列表具体说明:

这个题目对狄加特斯拉的算法要求更高了一个境界,写起来十分吃力,所以借鉴了很多大佬们的思路和代码,编译错误还是环境问题。
部分正确是因为少了一个很关键的赋值环节,发现之后添上就改正了
3.截图本周题目集的PTA最后排名(3分)
本次题目集总分:310分
3.1 PTA排名(截图带自己名字的排名)

3.2 我的总分:105
本题评分规则:
(1)PTA总分310分:3分(全部题目都做)
(2)PTA总分在250分--310分:2.5分(大部分做完1)
(3)PTA总分在200--250分:2分(大部分做完2)
(4)PTA总分在150--200分:1.5分
(5)PTA总分在60分-150分:1分
(6)PTA总分在60分以下:0分 4. 阅读代码(必做,1分)
本次为必做
天梯地图:
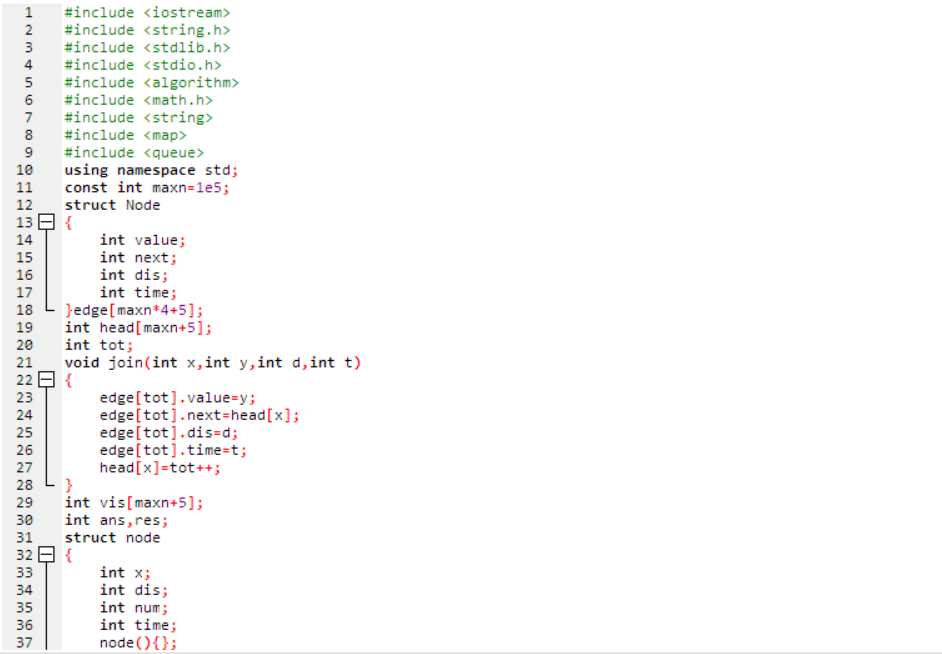
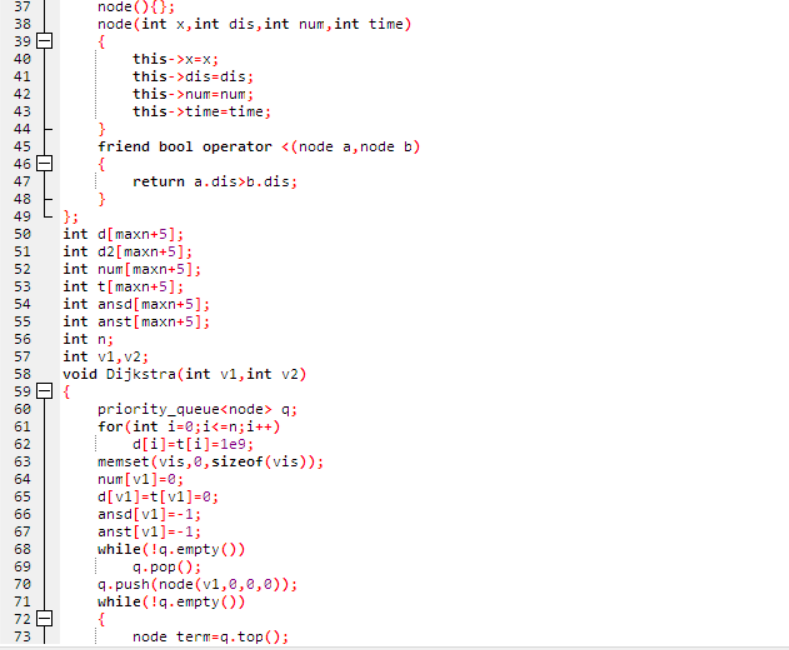

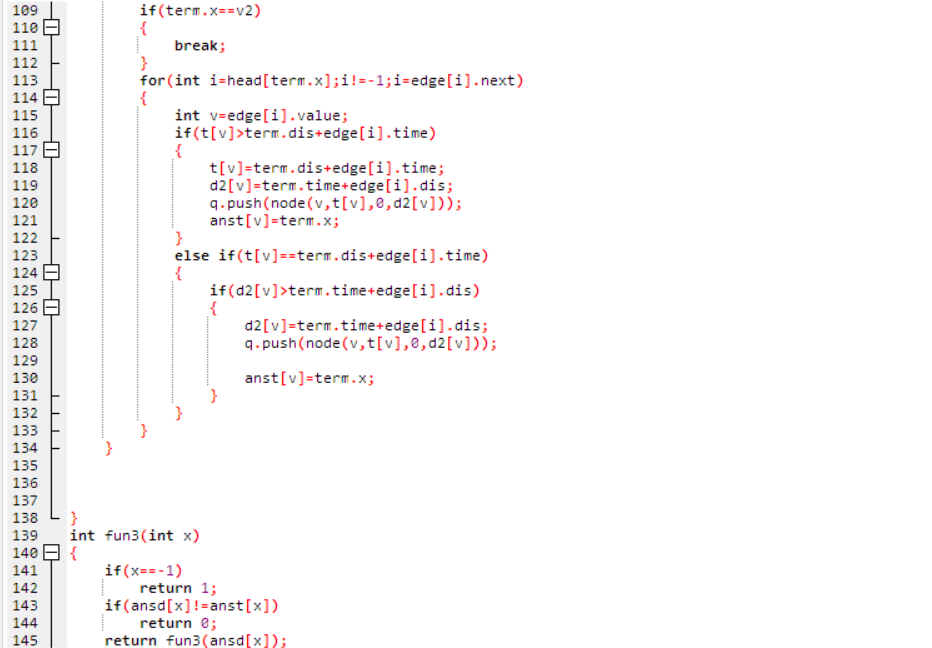
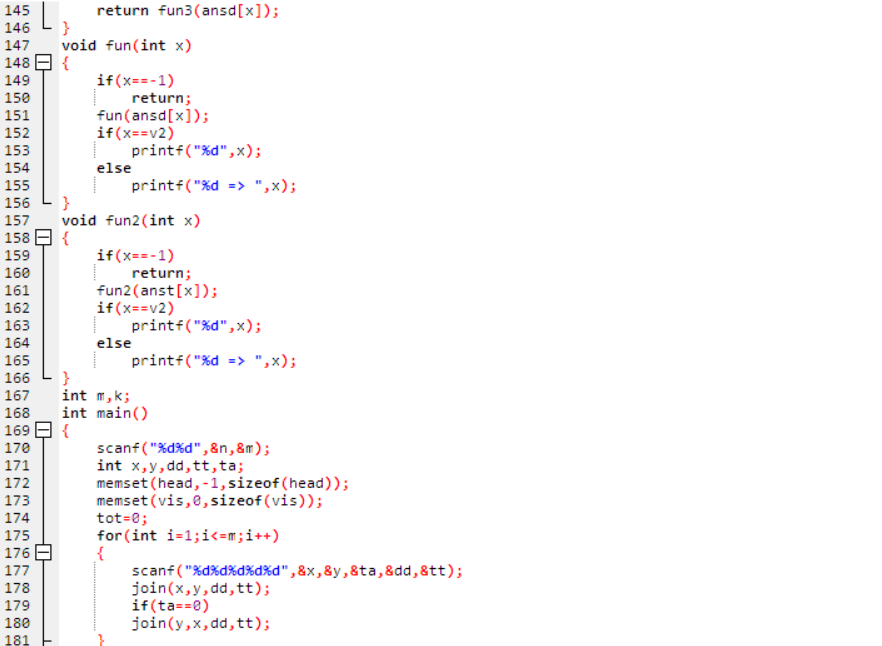
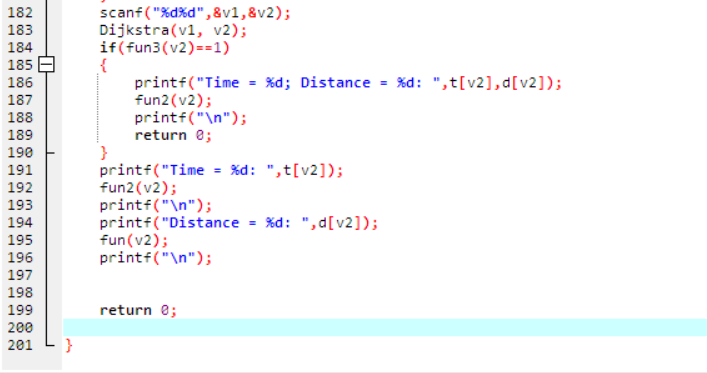
这个代码是真的很长,但是仔细一看子函数分工都很明确,其中的调用技巧十分成熟,先mark。好好学习参考。





