斜率优化动态规划
例题:HNOI2008 玩具装箱
设此时有决策a和b,其中a≤b
若决策a优于决策b,则
分离变量,移项整理
因为对于每个i来说,![]() 是常量,所以
是常量,所以![]() 是判断决策优劣程度的充要标准。
是判断决策优劣程度的充要标准。
那么现在考虑决策a,b,c,其中a≤b≤c
这意味着a比b优,b又比c优,所以a最优,应该选a,不能选b。
这意味着b比a优,c又比b优,所以c最优,应该选c,不能选b。
这意味着a比b优,c也比b优,所以不是a最优就是c最优,反正b不是最优,还是不能选b。
那么就维护一个单调队列:
1、对于队尾:设a,b,c(a≤b≤c)是队尾的三个元素,那么判断![]() 和
和![]() ,若
,若![]() ,就把c向前一位,也就是覆盖掉b。如此循环判断直到
,就把c向前一位,也就是覆盖掉b。如此循环判断直到![]() 或元素少于三个。
或元素少于三个。
2、对于队头:设a,b(a≤b)是队头的两个元素,因为![]() ,且
,且![]() 是单调的(如果不单调那只能用平衡树维护了),所以
是单调的(如果不单调那只能用平衡树维护了),所以![]() 那么就是说a对于以后的任意一个状态都不是最优决策,所以a出队。
那么就是说a对于以后的任意一个状态都不是最优决策,所以a出队。
通过以上两种维护,每次转移i时选队头就是最优决策了。
复杂度从O(n2)降到了O(n)。
wsc500原创,转载请注明出处。请注明 出自http://www.cnblogs.com/loveidea/


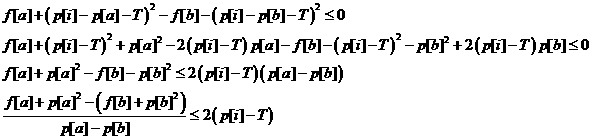
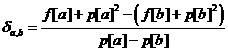

 浙公网安备 33010602011771号
浙公网安备 33010602011771号