[Leetcode] unique paths 独特路径

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

Above is a 3 x 7 grid. How many possible unique paths are there?

Note: m and n will be at most 100.

 题意：从左上角到右下角，总共有多少条路径。

思路：动态规划。维护一个二维数组，dp[i][j]代表到达第i 行j列有几种方法。转移方程为：dp[i][j]=dp[i-1][j]+dp[i][j-1]。如图：

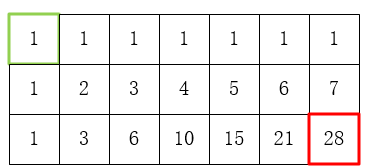
代码如下：

class Solution {
public:
    int uniquePaths(int m, int n) 
    {
        if(m=0||n=0)    return 1;
        int dp[m][n];
        dp[0][0]=1;

        for(int i=1;i<m;++i)
            dp[i][0]=1;
        for(int i=1;i<n;++i)  
            dp[0][i]=1;

        for(int i=1;i<m;++i)
        {
            for(int j=1;j<n;++j)
            {
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }  
        return dp[m-1][n-1];
    }
};

 

同种思路：另一种方法，使用滚动数组，利用一个一维数组实现上述过程，改动的思路是，二维数组中的dp[i][j]的值是表中的前一个和上一个，可以看成一维数组中的，前一个和其本身。

class Solution {
public:
    int uniquePaths(int m, int n) 
    {
        vector<int> dp(n,1);
        for(int i=1;i<m;++i)
        {
            for(int j=1;j<n;++j)
            {
                dp[j]+=dp[j-1];
            }
        }
        return dp[n-1];
    }
};