POJ2488-A Knight's Journey（DFS+回溯）

题目链接：http://poj.org/problem?id=2488

A Knight's Journey

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 36695		Accepted: 12462

Description

Background 
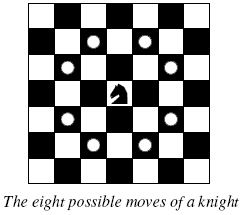
The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey 
around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 * 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans? 

Problem 
Find a path such that the knight visits every square once. The knight can start and end on any square of the board.

Input

The input begins with a positive integer n in the first line. The following lines contain n test cases. Each test case consists of a single line with two positive integers p and q, such that 1 <= p * q <= 26. This represents a p * q chessboard, where p describes how many different square numbers 1, . . . , p exist, q describes how many different square letters exist. These are the first q letters of the Latin alphabet: A, . . .

Output

The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing the lexicographically first path that visits all squares of the chessboard with knight moves followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number. 
If no such path exist, you should output impossible on a single line.

Sample Input

3
1 1
2 3
4 3

Sample Output

Scenario #1:
A1

Scenario #2:
impossible

Scenario #3:
A1B3C1A2B4C2A3B1C3A4B2C4

题目大意： 任选一个起点，按照国际象棋马的跳法，不重复的跳完整个棋盘，如果有多种路线则选择字典序最小的路线（路线是点的横纵坐标的集合，注意棋盘的横坐标的用大写字母，纵坐标是数字)

题目分析： 

1. 应该看到这个题就可以想到用DFS，当首先要明白这个题的意思是能否只走一遍（不回头不重复）将整个地图走完，而普通的深度优先搜索是一直走，走不通之后沿路返回到某处继续深搜。所以这个题要用到的回溯思想，如果不重复走一遍就走完了，做一个标记，算法停止；否则在某种DFS下走到某一步时按马跳的规则无路可走而棋盘还有为走到的点，这样我们就需要撤消这一步，进而尝试其他的路线（当然其他的路线也可能导致撤销），而所谓撤销这一步就是在递归深搜返回时重置该点，以便在当前路线走一遍行不通换另一种路线时，该点的状态是未访问过的，而不是像普通的DFS当作已经访问了。

2. 如果有多种方式可以不重复走一遍的走完，需要输出按字典序最小的路径，而注意到国际象棋的棋盘是列为字母，行为数字，如果能够不回头走一遍的走完，一定会经过A1点，所以我们应该从A1开始搜索，以确保之后得到的路径字典序是最小的（也就是说如果路径不以A1开始，该路径一定不是字典序最小路径），而且我们应该确保优先选择的方向是字典序最小的方向，这样我们最先得到的路径就是字典序最小的。

参考代码：

 

#include <cstdio>
#include <cstring>

using namespace std;

const int MAX_N = 27;
//字典序最小的行走方向
const int dx[8] = {-1, 1, -2, 2, -2, 2, -1, 1}; 
const int dy[8] = {-2, -2, -1, -1, 1, 1, 2, 2};
bool visited[MAX_N][MAX_N];
struct Step{
    char x, y;
} path[MAX_N];
bool success;           //是否成功遍历的标记
int cases, p, q;

void DFS(int x, int y, int num);

int main()
{
    scanf("%d", &cases);
    for (int c = 1; c <= cases; c++)
    {
        success = false;
        scanf("%d%d", &p, &q);
        memset(visited, false, sizeof(visited));
        visited[1][1] = true;    //起点
        DFS(1, 1, 1);              
        printf("Scenario #%d:\n", c);
        if (success)
        {
            for (int i = 1; i <= p * q; i++)
                printf("%c%c", path[i].y, path[i].x);
            printf("\n");
        }
        else
            printf("impossible\n");
        if (c != cases)
            printf("\n");      //注意该题的换行
    }
    return 0;
}

void DFS(int x, int y, int num)
{
    path[num].y = y + 'A' - 1;   //int 转为 char
    path[num].x = x + '0';
    if (num == p * q) 
    {
        success = true;
        return;
    }
    for (int i = 0; i < 8; i++)
    {
        int nx = x + dx[i];
        int ny = y + dy[i];
        if (0 < nx && nx <= p && 0 < ny && ny <= q
            && !visited[nx][ny] && !success)
        {
            visited[nx][ny] = true;
            DFS(nx, ny, num+1);
            visited[nx][ny] = false;    //撤销该步
        }
    }
}