04-树4. Root of AVL Tree-平衡查找树AVL树的实现

　　对于一棵普通的二叉查找树而言，在进行多次的插入或删除后，容易让树失去平衡，导致树的深度不是O(logN)，而接近O(N),这样将大大减少对树的查找效率。一种解决办法就是要有一个称为平衡的附加的结构条件：任何节点的深度均不得过深。有一种最古老的平衡查找树，即AVL树。

　　AVL树是带有平衡条件的二叉查找树。平衡条件是每个节点的左子树和右子树的高度最多差1的二叉查找树（空树的高度定义为-1）。相比于普通的二叉树，AVL树的节点需要增加一个变量保存节点高度。AVL树的节点声明如下：

typedef struct TreeNode *AvlTree;
typedef struct TreeNode *Position;
struct TreeNode
{
    int Data;
    AvlTree Left;
    AvlTree Right;
    int Height;        //保存节点高度    
};

　　只有一个节点的树显然是AVL树，之后我们向其插入节点。然而在插入过程中可能破坏AVL树的特性，因此我们需要对树进行简单的修正，即AVL树的旋转。

　　设a节点在插入下一个节点后会失去平衡，这种插入可能出现四种情况：

　　1. 对a的左儿子的左子树进行一次插入。（左-左）

　　2. 对a的左儿子的右子树进行一次插入。（左-右）

　　3. 对a的右儿子的左子树进行一次插入。（右-左）

　　4. 对a的右儿子的右子树进行一次插入。（右-右）

　　情形1和4，情形2和3分别是关于A节点的镜像对称，故在理论上是两种情况，而编程具体实现还是需要考虑四种。

　　单旋转--情形1和4：

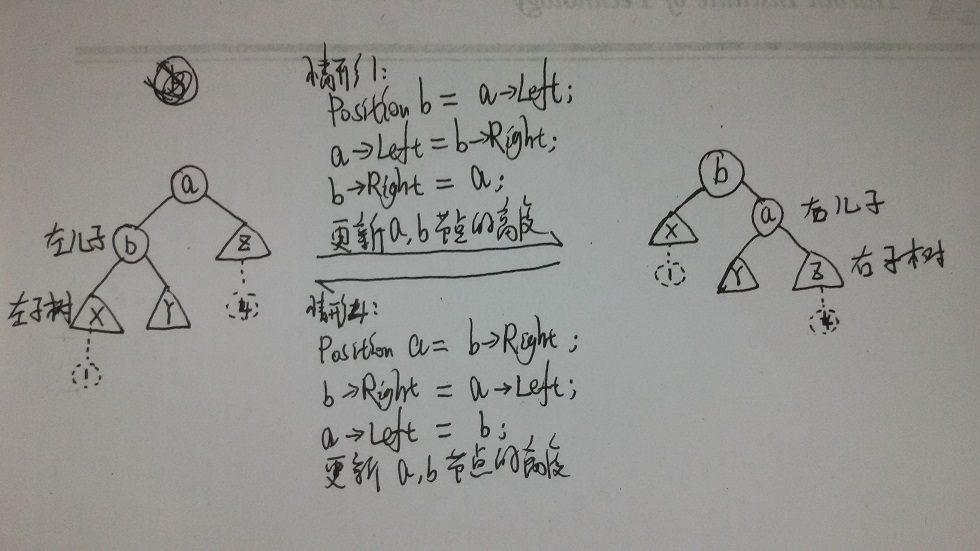
　　双旋转--情形2和3：

　　情形2和3就是向上图中的子树Y插入一个节点，由上图可知，无论是左单旋还是右单旋都无法改变子树Y的高度。解决办法是再将子树Y分解成根节点和相应的左子树和右子树，然后对相应的节点做相应的旋转，如下图：

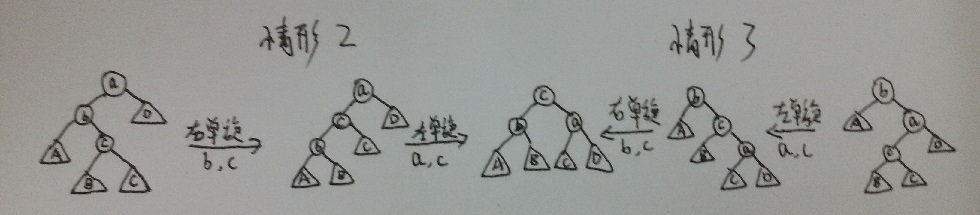
　　下面一个题即是考察AVL树的旋转：题目来源：http://www.patest.cn/contests/mooc-ds/04-%E6%A0%914

An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.

    

 

    

Now given a sequence of insertions, you are supposed to tell the root of the resulting AVL tree.

 

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (<=20) which is the total number of keys to be inserted. Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print ythe root of the resulting AVL tree in one line.

Sample Input 1:

5
88 70 61 96 120

Sample Output 1:

70

Sample Input 2:

7
88 70 61 96 120 90 65

Sample Output 2:

88

题目大意是先输入一个整数N，然后依次输入N个节点的值，以此建立AVL树，最后输出AVL树的根节点的值。

代码如下：

#include <cstdio>
#include <cstdlib>

typedef struct TreeNode *AvlTree;
typedef struct TreeNode *Position;
struct TreeNode
{
    int Data;
    AvlTree Left;
    AvlTree Right;
    int Height;
};

AvlTree Insert(int x, AvlTree T);   //插入新节点，必要时调整
Position SingleRotateWithLeft(Position a);    //左单旋
Position SingleRotateWithRight(Position b);   //右单旋
Position DoubleRotateWithLeft(Position a);    //左右旋
Position DoubleRotateWithRight(Position b);   //右左旋

int Max(int x1, int x2);      //返回两个int中较大的
int Height(Position P);     //返回一个节点的高度

int main()
{
    int n, x;
    AvlTree T = NULL;

    scanf("%d", &n);
    for (int i = 0; i < n; i++)
    {
        scanf("%d", &x);
        T = Insert(x, T);
    }
    printf("%d\n", T->Data);    //打印根节点的值

    return 0;
}

AvlTree Insert(int x, AvlTree T)
{
    if (T == NULL)
    {
        T = (AvlTree)malloc(sizeof(struct TreeNode));
        T->Data = x;
        T->Left = T->Right = NULL;
        T->Height = 0;
    }
    else if (x < T->Data)   //向左子树插入
    {
        T->Left = Insert(x, T->Left);
        if (Height(T->Left) - Height(T->Right) == 2)    //需调整
        {
            if (x < T->Left->Data)
                T = SingleRotateWithLeft(T);
            else
                T = DoubleRotateWithLeft(T);
        }
    }
    else if (x > T->Data)   //向右子树插入
    {
        T->Right = Insert(x, T->Right);
        if (Height(T->Right) - Height(T->Left) == 2)    //需调整
        {
            if (x > T->Right->Data)
                T = SingleRotateWithRight(T);
            else
                T = DoubleRotateWithRight(T);
        }
    }
    /*else值为x的节点已经存在树中，无需插入*/

    /*更新节点高度*/
    T->Height = Max(Height(T->Left), Height(T->Right)) + 1;
    return T;
}

Position SingleRotateWithLeft(Position a)
{
    Position b = a->Left;
    a->Left = b->Right;
    b->Right = a;
    //更新a, b节点高度
    a->Height = Max(Height(a->Left), Height(a->Right)) + 1;
    b->Height = Max(Height(b->Left), Height(b->Right)) + 1;

    return b;      /*新的根节点*/
}

Position SingleRotateWithRight(Position b)
{
    Position a = b->Right;
    b->Right = a->Left;
    a->Left = b;
    //更新a,b节点高度
    a->Height = Max(Height(a->Left), Height(a->Right)) + 1;
    b->Height = Max(Height(b->Left), Height(b->Right)) + 1;
    return a;       /*新的根节点*/
}

Position DoubleRotateWithLeft(Position a)
{
    a->Left = SingleRotateWithRight(a->Left);
    return SingleRotateWithLeft(a);
}

Position DoubleRotateWithRight(Position b)
{
    b->Right = SingleRotateWithLeft(b->Right);
    return SingleRotateWithRight(b);
}

int Max(int x1, int x2)
{
    return (x1 > x2) ? x1 : x2;
}

int Height(Position P)
{
    if (P == NULL)  //空节点高度为-1
        return -1;
    return P->Height;
}

 

　　需要注意的细节是我们需要快速得到一个节点（包括空节点）的高度，所以我们需要些一个函数来处理空节点（空指针）的情况，而不是简单的Position->Height。