ann搜索算法（Approximate Nearest Neighbor）

ANN的方法分为三大类：基于树的方法、哈希方法、矢量量化方法。brute-force搜索的方式是在全空间进行搜索，为了加快查找的速度，几乎所有的ANN方法都是通过对全空间分割，将其分割成很多小的子空间，在搜索的时候，通过某种方式，快速锁定在某一（几）子空间，然后在该（几个）子空间里做遍历。

1、基于树的方法

1.1 kd树

1.2 Annoy

Annoy是一个以树为数据结构的近似最近邻搜索库，并用在Spotify的推荐系统中。Annoy的核心是不断用选取的两个质心的法平面对空间进行分割，最终将每一个区分的子空间里面的样本数据限制在K以内。对于待插入的样本$x_i$，从根节点依次使用法向量跟$x_i$做内积运算，从而判断使用法平面的哪一边（左子树or右子树）。对于查询向量$q_i$，采用同样的方式（在树结构上体现为从根节点向叶子节点递归遍历），即可定位到跟$q_i$在同一个子空间或者邻近的子空间的样本，这些样本即为$q_i$近邻。为了提高查询的召回，Annoy采用建立多棵树的方式。

 

2、哈希方法

 

3、矢量量化方法

矢量量化方法，即vector quantization，其具体定义为：将一个向量空间中的点用其中的一个有限子集来进行编码的过程。在矢量量化编码中，关键是码本的建立和码字搜索算法。比如常见的聚类算法，就是一种矢量量化方法。而在ANN近似最近邻搜索中，向量量化方法又以乘积量化(PQ, Product Quantization)最为典型。 

PQ乘积量化的核心思想还是聚类，或者说具体应用到ANN近似最近邻搜索上，K-Means是PQ乘积量化子空间数目为1的特例。PQ乘积量化生成码本和量化的过程可以用如下图示来说明：

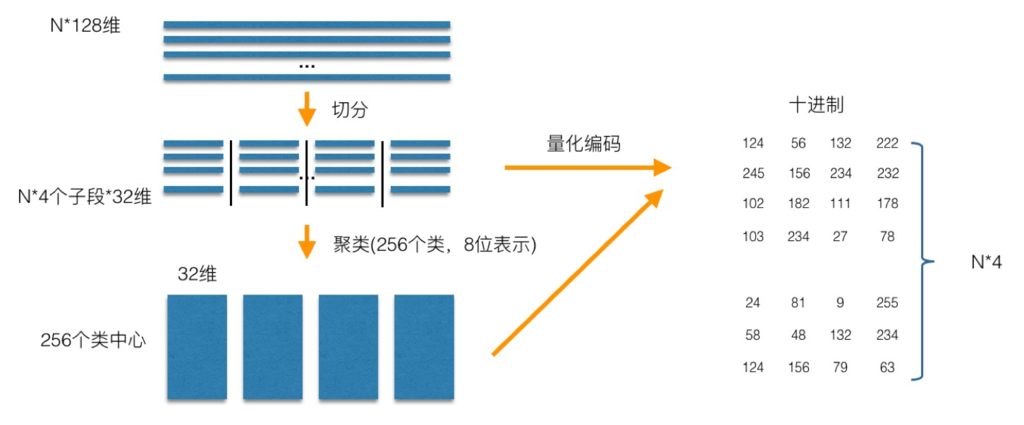
在训练阶段，针对N个训练样本，假设样本维度为128维，我们将其切分为4个子空间，则每一个子空间的维度为32维，然后我们在每一个子空间中，对子向量采用K-Means对其进行聚类(图中示意聚成256类)，这样每一个子空间都能得到一个码本。这样训练样本的每个子段，都可以用子空间的聚类中心来近似，对应的编码即为类中心的ID。如图所示，通过这样一种编码方式，训练样本仅使用的很短的一个编码得以表示，从而达到量化的目的。对于待编码的样本，将它进行相同的切分，然后在各个子空间里逐一找到距离它们最近的类中心，然后用类中心的id来表示它们，即完成了待编码样本的编码。

在查询阶段，PQ同样在计算查询样本与dataset中各个样本的距离，只不过这种距离的计算转化为间接近似的方法而获得。PQ乘积量化方法在计算距离的时候，有两种距离计算方式，一种是对称距离，另外一种是非对称距离。非对称距离的损失小(也就是更接近真实距离)，实际中也经常采用这种距离计算方式。下面过程示意的是查询样本来到时，以非对称距离的方式(红框标识出来的部分)计算到dataset样本间的计算示意：

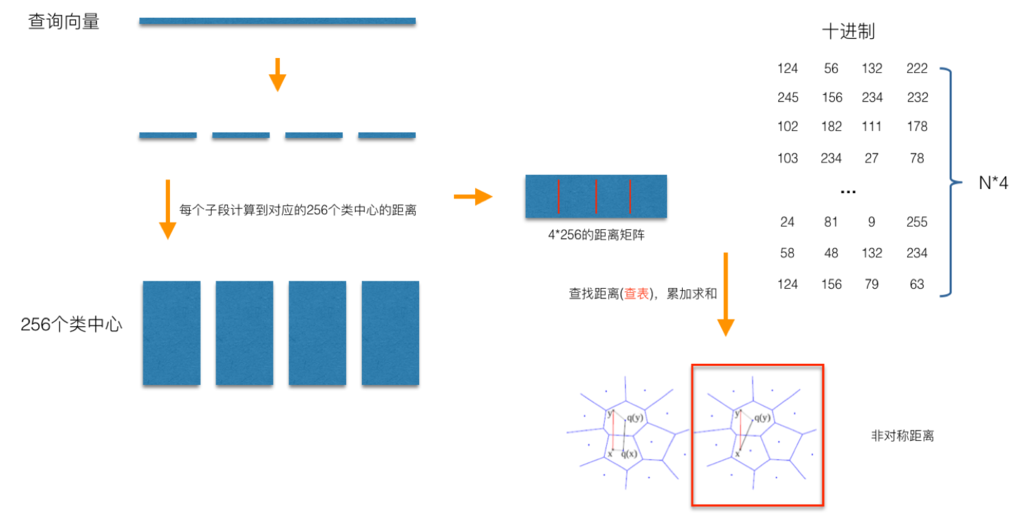
具体地，查询向量来到时，按训练样本生成码本的过程，将其同样分成相同的子段，然后在每个子空间中，计算子段到该子空间中所有聚类中心得距离，如图中所示，可以得到4*256个距离，这里为便于后面的理解说明，小白菜就把这些算好的距离称作距离池。在计算库中某个样本到查询向量的距离时，比如编码为(124, 56, 132, 222)这个样本到查询向量的距离时，我们分别到距离池中取各个子段对应的距离即可，比如编码为124这个子段，在第1个算出的256个距离里面把编号为124的那个距离取出来就可，所有子段对应的距离取出来后，将这些子段的距离求和相加，即得到该样本到查询样本间的非对称距离。所有距离算好后，排序后即得到我们最终想要的结果。

从上面这个过程可以很清楚地看出PQ乘积量化能够加速索引的原理：即将全样本的距离计算，转化为到子空间类中心的距离计算。比如上面所举的例子，原本brute-force search的方式计算距离的次数随样本数目N成线性增长，但是经过PQ编码后，对于耗时的距离计算，只要计算4*256次，几乎可以忽略此时间的消耗。另外，从上图也可以看出，对特征进行编码后，可以用一个相对比较短的编码来表示样本，自然对于内存的消耗要大大小于brute-force search的方式。 

在某些特殊的场合，我们总是希望获得精确的距离，而不是近似的距离，并且我们总是喜欢获取向量间的余弦相似度（余弦相似度距离范围在[-1,1]之间，便于设置固定的阈值），针对这种场景，可以针对PQ乘积量化得到的前top@K做一个brute-force search的排序。

倒排乘积量化

倒排PQ乘积量化(IVFPQ)是PQ乘积量化的更进一步加速版。其加速的本质逃不开小白菜在最前面强调的是加速原理：brute-force搜索的方式是在全空间进行搜索，为了加快查找的速度，几乎所有的ANN方法都是通过对全空间分割，将其分割成很多小的子空间，在搜索的时候，通过某种方式，快速锁定在某一（几）子空间，然后在该（几个）子空间里做遍历。在上一小节可以看出，PQ乘积量化计算距离的时候，距离虽然已经预先算好了，但是对于每个样本到查询样本的距离，还是得老老实实挨个去求和相加计算距离。但是，实际上我们感兴趣的是那些跟查询样本相近的样本（小白菜称这样的区域为感兴趣区域），也就是说老老实实挨个相加其实做了很多的无用功，如果能够通过某种手段快速将全局遍历锁定为感兴趣区域，则可以舍去不必要的全局计算以及排序。倒排PQ乘积量化的”倒排“，正是这样一种思想的体现，在具体实施手段上，采用的是通过聚类的方式实现感兴趣区域的快速定位，在倒排PQ乘积量化中，聚类可以说应用得淋漓尽致。

倒排PQ乘积量化整个过程如下图所示：

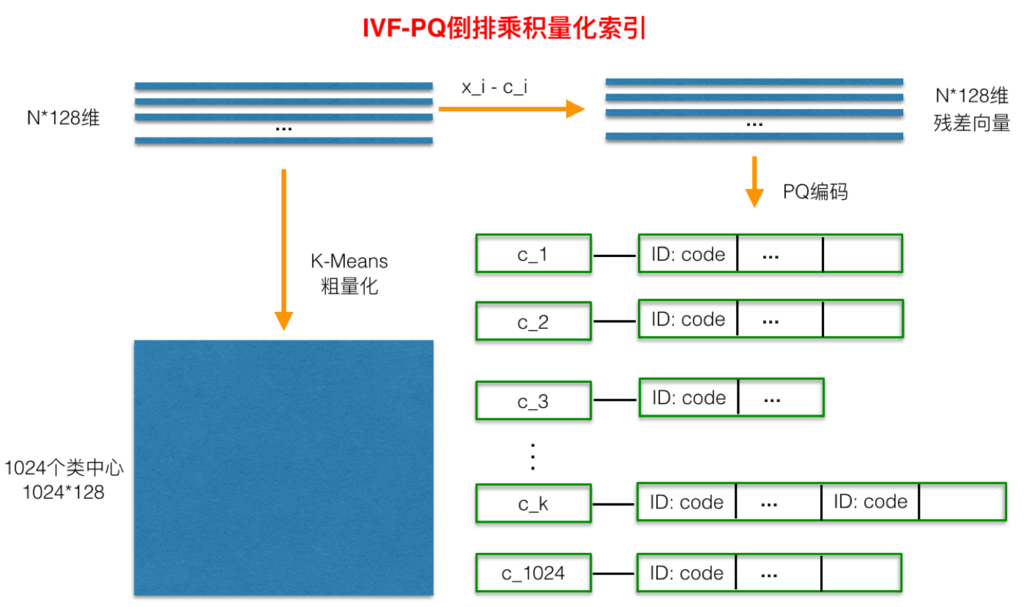
在PQ乘积量化之前，增加了一个粗量化过程。具体地，先对N个训练样本采用K-Means进行聚类，这里聚类的数目一般设置得不应过大，一般设置为1024差不多，这种可以以比较快的速度完成聚类过程。得到了聚类中心后，针对每一个样本x_i，找到其距离最近的类中心c_i后，两者相减得到样本x_i的残差向量(x_i-c_i)，后面剩下的过程，就是针对(x_i-c_i)的PQ乘积量化过程，此过程不再赘述。

在查询的时候，通过相同的粗量化，可以快速定位到查询向量属于哪个c_i（即在哪一个感兴趣区域），然后在该感兴趣区域按上面所述的PQ乘积量化距离计算方式计算距离。

 

 

参考：

https://yongyuan.name/blog/ann-search.html