【树论 2】Kruskal 的学习和使用
Tips:本题解是【随便搞搞 1】Prim算法的学习和使用 的姊妹篇,希望先阅读Prim算法。
预习及预备知识:
克鲁斯卡尔(Kruskal)算法是实现图的最小生成树最常用的算法。
大家知道,存储图的方法有2种:邻接矩阵表示法、邻接表表示法;
这里介绍的是介于这两种之间的一种方法:边接存储法(即直接用边来存储图)
但是最小生成树是什么呢?
标准定义如下:在边子集所构成的树中,不但包括了连通图里的所有顶点,且其所有边的权值之和亦为最小。
听起来非常的带劲,我们就一起来探讨这一求最小生成树的算法!
Kruskal算法的三大特征:
●对于稠密图中求最小生成树优于Prim算法
●对于稀疏图中求最小生成树的时间复杂度O(n+m log m)
●标准Kruskal算法流程包含并查集的部分知识
算法思想:
先构造一个只含 n 个顶点、而边集为空的子图,把子图中各个顶点看成各棵树上的根结点,之后,从网的边集 E 中选取一条权值最小的边,若该条边的两个顶点分属不同的树,则将其加入子图,即把两棵树合成一棵树,反之,若该条边的两个顶点已落在同一棵树上,则不可取,而应该取下一条权值最小的边再试之。依次类推,直到森林中只有一棵树,也即子图中含有 n-1 条边为止。
时间复杂度为为O(e^2), 使用并查集优化后复杂度为 O(eloge),与网中的边数有关,适用于求边稀疏的网的最小生成树。
克鲁斯卡尔算法从另一途径求网的最小生成树。假设连通网N=(V,{E}),则令最小生成树的初始状态为只有n个顶点而无边的非连通图T=(V,{∮}),图中每个顶点自成一个连通分量。在E中选择代价最小的边,若该边依附的顶点落在T中不同的连通分量上,则将此边加入到T中,否则舍去此边而选择下一条代价最小的边。依次类推,直至T中所有顶点都在同一连通分量上为止。
图例1:
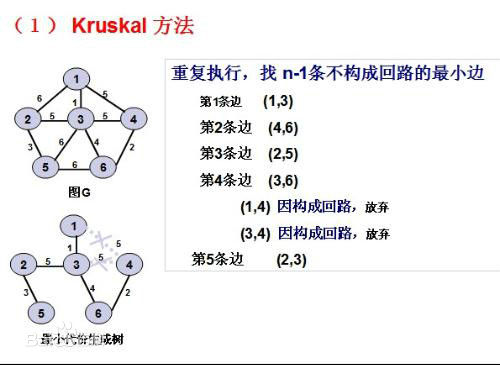
引入集合到集合的距离:对于两个集合A,B;集合A中元素和B中元素各不相同
集合A中所有元素到集合B中所有元素的距离最小值定义为集合到集合的距离
贪心方法:每一次只要连接集合到集合距离最小的两个集合,反复n-1次得出的为最小生成树
对于上例,图为依照克鲁斯卡尔算法构造一棵最小生成树的过程。代价分别为1,2,3,4的四条边由于满足上述条件,则先后被加入到T中,代价为5的两条边(1,4)和(3,4)被舍去。因为它们依附的两顶点在同一连通分量上,它们若加入T中,则会使T中产生回路,而下一条代价(=5)最小的边(2,3)联结两个连通分量,则可加入T。因此,构造成一棵最小生成树。
图例2:
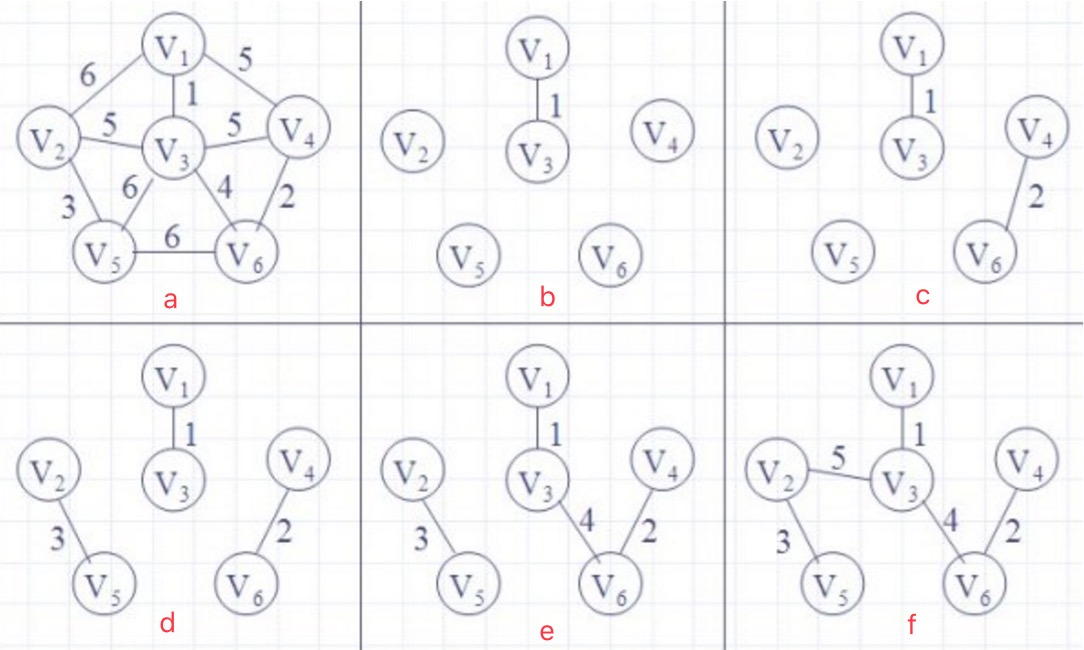
a图中是输入的一个无向图;
b中连接集合到集合距离最小的两个集合1 3,{1,3}就是一棵最小生成树;
c图连接4 6,此时图中有两个元素大于等于2个的连通分支{1,3}{4,6}分别是最小生成树;
d图连接2 3,此时图中有三个元素大于等于2个的连通分支{1,3}{4,6}{2,5}分别是最小生成树;
e图连接两个连通分支{1,3}{4,6},图中有两个元素大于等于2个的连通分支{2,5}{1,3,4,6}分别是最小生成树;
f图连接两个连通分支{2,5}{1,3,4,6},图中有一个元素大于等于2个的连通分支{1,2,3,4,5,6}是最小生成树;
算法完成连通分支{1,2,3,4,5,6}就是关于全图a的最小生成树;
模板分析:
题目描述
如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出orz
输入输出格式
输入格式:
第一行包含两个整数N、M,表示该图共有N个结点和M条无向边。(N<=5000,M<=200000)
接下来M行每行包含三个整数Xi、Yi、Zi,表示有一条长度为Zi的无向边连接结点Xi、Yi
输出格式:
输出包含一个数,即最小生成树的各边的长度之和;如果该图不连通则输出orz
输入输出样例
输入样例#1:
4 5
1 2 2
1 3 2
1 4 3
2 3 4
3 4 3
输出样例#1:
7
说明
时空限制:1000ms,128M
数据规模:
对于20%的数据:N<=5,M<=20
对于40%的数据:N<=50,M<=2500
对于70%的数据:N<=500,M<=10000
对于100%的数据:N<=5000,M<=200000
样例解释:
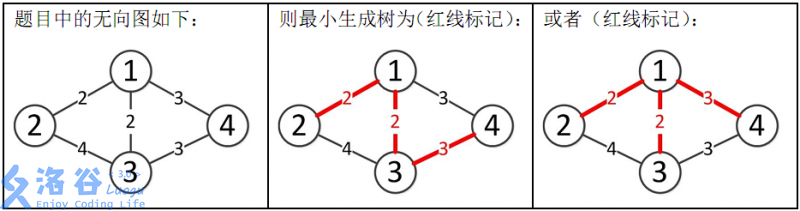
所以最小生成树的总边权为2+2+3=7
【分析】
对于样例,我们把1 2 3 4四点抽象为含有一个元素的子集{1}{2}{3}{4}
首先看到子集{1}{3}之间距离最小,且遍历越靠后,合并形成一个连通分支{1,3}{2}{4}
看到子集{2}{1,3}之间距离最小,合并形成一个连通分支{1,2,3}{4}
看到子集{1,2,3}{4}之间距离最小,合并形成一个连通分支{1,2,3,4}
看到连通分支{1,2,3,4}是全局的最小生成树,所以路径和为2+2+3=7
【实现】
type rec=record u,v,len:longint; end; var n,m,i:longint; a:array[0..200000]of rec; f:array[0..200000]of longint; procedure qsort(l,r:longint);//按照边权从大到小排序 var i,j,mid:longint; t:rec; begin i:=l; j:=r; mid:=a[(l+r)div 2].len; repeat while a[i].len<mid do inc(i); while a[j].len>mid do dec(j); if i<=j then begin t:=a[i]; a[i]:=a[j]; a[j]:=t; inc(i); dec(j); end; until i>=j; if j>l then qsort(l,j); if i<r then qsort(i,r); end; function father(x:longint):longint;//求x的father,学过的都看得懂 begin if f[x]=x then exit(x); f[x]:=father(f[x]); exit(father(f[x]));//加了路径压缩,快一点 end; procedure kruskal; var tot,cnt,i,fx,fy:longint; begin for i:=1 to m do f[i]:=i;//并查集赋初值 qsort(1,m);//快速排序 cnt:=0; tot:=0;//初值 for i:=1 to m do begin//遍历每条边 fx:=father(a[i].u); fy:=father(a[i].v);//求一条边的左右两个端点的father if fx<>fy then begin//判断如果不是同一father则这两个点在不同的子树中 f[fx]:=fy;//合并 inc(cnt);//连了这条边u<--->v tot:=tot+a[i].len;//加上这条边的权值 end; if cnt=n-1 then break;//加到n-1就跳 end; if cnt<>n-1 then writeln('orz')//不符合最小生成树的边=点数-1就是不合法 else writeln(tot);//输出各边权值和 end; begin readln(n,m); for i:=1 to m do readln(a[i].u,a[i].v,a[i].len); kruskal; end.
时间复杂度的推导:
初始化 所有点各自为一个森林 这一步是O(n)的
并且把边集进行从小到大排序,这一步如果使用快速排序或者堆排序是O(mlogm)
然后在这一片森林中添加边,我们知道n个点构成的树是有n-1条边,因此需要执行n-1次以下操作
从已经排序的边序列中,挑选长度最短的,且两端不在同一棵树中的一条边,判断是否是同一棵树是利用并查集进行查询,挑出这一条边之后,把两个端点代表的树合并为一棵,即并查集的合并,这也是O(1)的
注意到在选取边的过程中,只要挑选其中的n-1条,因此挑选边的n-1次挑选边的复杂度之和是O(m)的(可以理解为看最后一条连接的边在序列的第几条,最坏情况就是最后一条才能使n个点连通,因此最坏复杂度是O(m)
因此总复杂度为O(n+mlogm)
应用:
有了这一个神奇的算法我们能干什么呢?
村庄修路,网络铺设,关于最小生成树的问题,应用比较广,学科范围广,这里给一个模板题:
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 6623 | Accepted: 3608 |
Description
Your task is to design the network for the area, so that there is a connection (direct or indirect) between every two points (i.e., all the points are interconnected, but not necessarily by a direct cable), and that the total length of the used cable is minimal.
Input
The maximal number of points is 50. The maximal length of a given route is 100. The number of possible routes is unlimited. The nodes are identified with integers between 1 and P (inclusive). The routes between two points i and j may be given as i j or as j i.
Output
Sample Input
1 0 2 3 1 2 37 2 1 17 1 2 68 3 7 1 2 19 2 3 11 3 1 7 1 3 5 2 3 89 3 1 91 1 2 32 5 7 1 2 5 2 3 7 2 4 8 4 5 11 3 5 10 1 5 6 4 2 12 0
Sample Output
0 17 16 26
参见上面的程序,prim注意有重边的处理,但是Kruskal不用担心重边的问题



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步