【枚举Day1】20170529-2枚举算法专题练习 题目
20170529-2枚举算法专题练习
题解: http://www.cnblogs.com/ljc20020730/p/6918360.html
|
青岛二中日期 |
序号 |
题目名称 |
输入文件名 |
输出文件名 |
时限 |
内存 |
算法 |
难度 |
分类 |
|
081113 |
1 |
最大矩形 |
rectangle.in |
rectangle.out |
1s |
256MB |
枚举 |
1 |
02枚举 |
|
081031 |
2 |
回文 |
palin.in |
palin.out |
1s |
256MB |
枚举、优化 |
1 |
02枚举 |
|
081008 |
3 |
问题的设置 |
problemsetter.in |
problemsetter.out |
1s |
256MB |
排序+枚举 |
1 |
02枚举 |
|
081031 |
4 |
矩形着色 |
rectangles.in |
rectangles.out |
1s |
256MB |
枚举 |
2 |
02枚举 |
1.OneMoreRectangle一个矩形
【题目描述】
在一个平面上有一些矩形。矩形的边都与坐标轴平行。矩形允许相交、重叠。你的任务是,在平面上再放入一个边与坐标轴平行的矩形,且覆盖尽量多的已有矩形。
我们用四个整数来表示一个矩形,x1,y1,x2,y2,分别表示矩形的横纵坐标最小值、横纵坐标最大值。若矩形a的坐标为x1,y1,x2,y2,矩形A的坐标为X1,Y1,X2,Y2,则a能被A覆盖当且仅当X1<=x1<x2<=X2,且Y1<=y1<y2<=Y2。

【输入文件】第一行有三个整数n,X,Y,分别表示已有矩形个数、你要放入的矩形的边长(也就是X=X2-X1,Y=y2-y1)。你放入的矩形的大小必须同规定大小相同,位置由你决定。
接下来n行,每行4个整数x1,y1,x2,y2,表示已知矩形的坐标。
【输出文件】只有一个整数,表示你最多可以覆盖几个已有矩形。
【输入样例】
3 2 2
1 1 2 2
2 2 3 3
3 3 4 4
【输出样例】2
【数据规模和约定】
n<=50;
所有给定坐标的绝对值不超过109;
所有给定坐标保证x1<x2,y1<y2;
X和Y是不超过109的正整数。
2.Palindromes回文
【题目描述】一个回文串指的是,左右翻转后同原串相同的串。
给定一个数k(2<=k<=30000)和一个非空字符串S,S的长度不超过30000且只含小写字母。请你求出,S中有多少个不同的长度为k的回文子串。一个串的子串指的是它的连续的一部分。
本题中,两个长度为k的子串不同,当且仅当它们的起始位置不同。
【输入文件】第一行整数k。
第二行串S。
【输出文件】一个整数,表示不同的回文串个数。
【输入样例】
5
ababab
【输出样例】2
3.ProblemSetter(问题的设置)
【题目描述】
你要为一场比赛出题。从已有的题目中,你要选择三道不同的题:一道简单题、一道中等题,以及一道难题。每道题目都有一个整数的难度值。值越大,题目越难。假设E表示你选择的简单题的难度,M表示中等题难度,H表示难题难度,则必须保证E<=M<=H。你希望难度差尽量接近,也就是说,假设D1=M-E,D2=H-M,则|D1-D2|应该最小。如果有多种方案,选择其中E最小的。如果仍有多种方案,选择其中H最大的。如果还有多种方案,选择其中M最小的。
【输入文件】第一行一个整数n,表示题目数量。第二行n个整数,表示每道题的难度。
【输出文件】输出一行三个整数表示选择的题目难度。按照简单-中等-困难的顺序输出。中间用一个空格隔开。行尾不要有空格。
【输入样例】
5
1 2 3 4 5
【输出样例】
1 3 5
【样例说明】
此时,D1=D2=2。
【数据规模和约定】
3<=n<=50
难度是不超过1000的正整数。
4.ColoringRectangles着色的矩形
【题目描述】
在平面中给定N个与坐标轴平行的矩形,第i个矩形的左下角坐标是(x1[i],y1[i]),右上角坐标是(x2[i],y2[i])。
你的任务是从中选择K个矩形,使得所选矩形可视面积最大。如果一些矩形有重叠,那么重叠部分只有编号最大的矩形才可视。换句话说,编号大的矩形“盖”在编号小的矩形之上。请你输出选择的K个矩形的编号。如果有多种方法,输出字典序最小的一组。
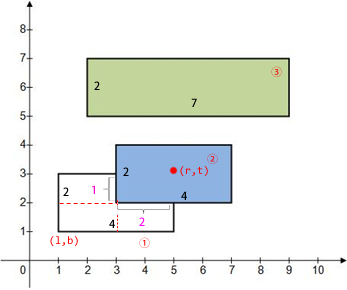
【输入文件】
第一行两个整数N,K。
第二行N个整数,表示x1[0]..x1[N-1]。
第三行N个整数,表示y1[0]..y1[N-1]。
第四行N个整数,表示x2[0]..x2[N-1]。
第五行N个整数,表示y2[0]..y2[N-1]。
【输出文件】
一行K个非负整数,表示选择的矩形的编号。编号之间用一个空格隔开。
【输入样例】
3 2
1 3 2
1 2 5
5 7 9
3 4 7
【输出样例】
1 2
【样例说明】
选择矩形0,1,面积为6+8=14
选择矩形0,2,面积为6+14=20
选择矩形1,2,面积为8+14=22。
【数据规模和约定】
1<=N<=50
-10000<=所有坐标<=10000
对于任意i,x1[i]<x2[i],y1[i]<y2[i]

