大话数据结构之四(串)
串的定义
串是由零个或多个字符组成的有限序列,又名叫字符串
串中的字符数目n称为串的长度
零个字符的串称为空串
串的抽象数据类型

串的顺序存储结构

串我链式存储结构
一个结点可以存储一个字符也可以考虑存储多个字符,最后一个结点若是未被占满时,可以用#或其它非串值字符补全

朴素的模式匹配算法
对主串的每一个字符作为子串开头,与要匹配的字符进行匹配。对主串做大循环,每个字符开头做T的长度的小循环,直到匹配成功或全部遍历完成为止。
时间复杂度为O(n+m)
/* 返回子串T在主串S中第pos个字符之后的位置。若不存在,则函数返回值为0。 */ /* 其中,T非空,1≤pos≤StrLength(S)。 */ int Index(String S, String T, int pos) { int i = pos; /* i用于主串S中当前位置下标值,若pos不为1,则从pos位置开始匹配 */ int j = 1; /* j用于子串T中当前位置下标值 */ while (i <= S[0] && j <= T[0]) /* 若i小于S的长度并且j小于T的长度时,循环继续 */ { if (S[i] == T[j]) /* 两字母相等则继续 */ { ++i; ++j; } else /* 指针后退重新开始匹配 */ { i = i-j+2; /* i退回到上次匹配首位的下一位 */ j = 1; /* j退回到子串T的首位 */ } } if (j > T[0]) return i-T[0]; else return 0; }
利用上面的算法,假设我们要从主串goodgoogle中找到google,则需要下面的步骤
想想如果我们要在主串S="00000000000000000000000000000000000000000000000000001",而要匹配的子串T=“0000000001”
也就是说T串需要在S串的前40个位置都需要判断10次并得到不匹配的结论,直到第41位才全部匹配相等


因此最坏的情况的时间复杂度为O(((n-m)+1)*m)
KMP模式匹配算法原理
如果主串S="abcdefgab",要匹配的子串T="abcdex"
如果用朴素算法的话,则匹配的流程图如下所示:

细想一下,子串T中“abcdex” 首字母a与后面的串“bcdex”中的任意一个字符都不相等,既然a不与自己后面的子串中任何一个字符相等,那么对于上图1来说,前五个字符分别相等,意味着子串T的首字符a不可能与s串的第2位到第5位的字符相等,也就是说在上图中2、3、4、5的判断都是多余的。
如果子串T中有与首字符相等的字符,也是可以省略一部分不必要的判断步骤的。
我们把T串各个位置的j值的变化定义为一个数组next,那么next的长度就是T串的长度

举例说明next数组值推导
KMP模式匹配算法实现代码
/* 通过计算返回子串T的next数组。 */ void get_next(String T, int *next) { int i,j; i=1; j=0; next[1]=0; while (i<T[0]) /* 此处T[0]表示串T的长度 */ { if(j==0 || T[i]== T[j]) /* T[i]表示后缀的单个字符,T[j]表示前缀的单个字符 */ { ++i; ++j; next[i] = j; } else j= next[j]; /* 若字符不相同,则j值回溯 */ } } /* 返回子串T在主串S中第pos个字符之后的位置。若不存在,则函数返回值为0。 */ /* T非空,1≤pos≤StrLength(S)。 */ int Index_KMP(String S, String T, int pos) { int i = pos; /* i用于主串S中当前位置下标值,若pos不为1,则从pos位置开始匹配 */ int j = 1; /* j用于子串T中当前位置下标值 */ int next[255]; /* 定义一next数组 */ get_next(T, next); /* 对串T作分析,得到next数组 */ while (i <= S[0] && j <= T[0]) /* 若i小于S的长度并且j小于T的长度时,循环继续 */ { if (j==0 || S[i] == T[j]) /* 两字母相等则继续,与朴素算法增加了j=0判断 */ { ++i; ++j; } else /* 指针后退重新开始匹配 */ j = next[j];/* j退回合适的位置,i值不变 */ } if (j > T[0]) return i-T[0]; else return 0; }
上面get_next的时间复杂度为O(m),而index_KMP中while循环的时间复杂度为O(n),所以整个算法的时间复杂度为O(n+m)
KMP模式匹配算法改进
比如主串S="aaaabcde",子串T="aaaaax",那么next数组值分别为012345
利用KMP算法比较的过程如下图所示:

当i=5,j=5时,b与a不相等,如上图1
j=next[5]=4,如上图2,b与第四个位置的a依然不等
j=next[4]=3,如上图3,...
细想一下,2、3、4、5步骤都是多余的,因为T串的第二、三、四、五位置的字符都与首位a相等,那么可以利用首位的next[1]的值去取代与它相等的字符后续的next[j]的值
改良版的KMP算法实现代码
/* 求模式串T的next函数修正值并存入数组nextval */ void get_nextval(String T, int *nextval) { int i,j; i=1; j=0; nextval[1]=0; while (i<T[0]) /* 此处T[0]表示串T的长度 */ { if(j==0 || T[i]== T[j]) /* T[i]表示后缀的单个字符,T[j]表示前缀的单个字符 */ { ++i; ++j; if (T[i]!=T[j]) /* 若当前字符与前缀字符不同 */ nextval[i] = j; /* 则当前的j为nextval在i位置的值 */ else nextval[i] = nextval[j]; /* 如果与前缀字符相同,则将前缀字符的 */ /* nextval值赋值给nextval在i位置的值 */ } else j= nextval[j]; /* 若字符不相同,则j值回溯 */ } }
nextval数组值推导

(具体分析图如下所示:

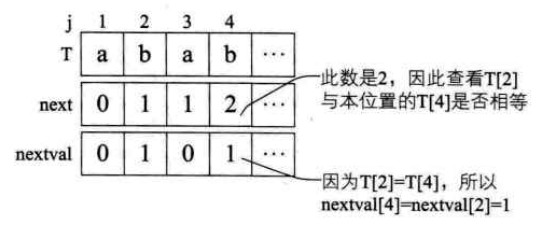 )
)
另外一个例子(看看你推导正确了没)

作者:静逸
出处:http://www.cnblogs.com/liyunhua
本文版权归作者和博客园所有,欢迎转载,转载请标明出处。
如果您觉得本篇博文对您有所收获,觉得小女子还算用心,请点击右下角的 [推荐],谢谢!











【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· go语言实现终端里的倒计时
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 分享 3 个 .NET 开源的文件压缩处理库,助力快速实现文件压缩解压功能!
· Ollama——大语言模型本地部署的极速利器
· DeepSeek如何颠覆传统软件测试?测试工程师会被淘汰吗?