向量空间模型(VSM)的余弦定理公式(cos)

相信很多学习向量空间模型(Vector Space Model)的人都会被其中的余弦定理公式所迷惑..

 

因为一看到余弦定理,肯定会先想起初中时的那条最简单的公式cosA=a/c(邻边比斜边),见下图:

但是,初中那条公式是只适用于直角三角形的,而在非直角三角形中,余弦定理的公式是:

cosA=(c² + b² - a²)/2bc

不过这条公式也和向量空间模型中的余弦定理公式不沾边,迷惑..

 

引用吴军老师的数学之美系列的余弦定理和新闻的分类里面的一段:

-------------------引用开始分界线------------------------

假定三角形的三条边为 a, b 和 c，对应的三个角为 A, B 和 C，那么角 A 的余弦

如果我们将三角形的两边 b 和 c 看成是两个向量，那么上述公式等价于

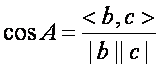
其中分母表示两个向量 b 和 c 的长度，分子表示两个向量的内积。

举一个具体的例子，假如新闻 X 和新闻 Y 对应向量分别是x1,x2,...,x64000 和y1,y2,...,y64000,

那么它们夹角的余弦等于

 

-------------------引用完毕分界线------------------------

 

高中那条公式又怎么会等价于向量那条公式呢?

原来它从高中的平面几何跳跃到大学的线性代数的向量计算..

关于线性代数中的向量和向量空间,可以参考下面两个页面:

Egwald Mathematics: Linear Algebra

Linear Algebra: Direction Cosines

 

在线性代数的向量计算的余弦定理中,

* 分子是两个向量的点积(wiki),点积的定理和计算公式:

The dot product of two vectors a = [a₁, a₂, … , a_n] and b = [b₁, b₂, … , b_n] is defined as:

 

点积(dot product),又叫内积,数量积..(Clotho注: product常见的是产品的意思,但在数学上是乘积的意思.)

 

* 分母是两个向量的长度相乘.这里的向量长度的计算公式也比较难理解.

假设是二维向量或者三维向量,可以抽象地理解为在直角坐标轴中的有向线段,如图:

d² = x² + y²   ->   d = sprt(x² + y²)

 

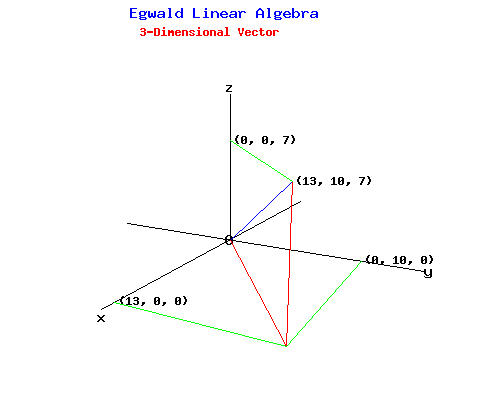
d² = x² + y² + z²   ->   d = sprt(x² + y² + z²)

 

三维以上的维度很难用图来表示,但是再多维度的向量,也仍然可以用这条公式来计算:

d_n² = x₁² + x₂² + .. + x_n²   ->   d_n = sprt(x₁² + x₂² + .. + x_n²)

 

在文本相似度计算中,向量中的维度x₁,x₂..x_n其实就是词项(term)的权重,一般就是词项的tf-idf值.

而这条看上去很抽象的公式,其实就是为了计算两篇文章的相似度.

 

文本相似度计算的处理流程是:

1.对所有文章进行分词

2.分词的同时计算各个词的tf值

3.所有文章分词完毕后计算idf值

4.生成每篇文章对应的n维向量(n是切分出来的词数,向量的项就是各个词的tf-idf值)

5.对文章的向量两篇两篇代入余弦定理公式计算,得出的cos值就是它们之间的相似度了