四元数研究

接着上一篇博客四元数研究：www.cnblogs.com/liuzhenbo/p/10749458.html

　　为了规避Ambiguity的问题，我们给出另一种表述方向的方法：轴角表示(Axis-Angle-Representation)。跟欧拉角不同的是，我们这次不再采取多次旋转的方式来找到目标方向，而是找到一根旋转轴，只通过绕这根轴旋转一次就可以得到目标方向。这样就不会产生Ambiguity了吗？是的，证明方法很简单，首先以目标矩阵原点为一角，三轴为三边建立一个立方体，这个立方体中通过原点的对角线就是我们要找的旋转轴，显然，这个旋转轴是唯一的，而我们知道，绕一个旋转轴旋转不同角度，对应的方向也是不同的（角度范围（角度范围 \left(-\pi, \pi\right] ），由此可见，空间中任一位置的轴角表示是唯一的，不存在Ambiguity的问题。旋转轴我们可以通过向量 \left[\begin{matrix}x\\y\\z\end{matrix}\right] 来表示，旋转角度我们可以通过一个度数 \theta 来表示，至此我们可以通过轴角表示 (axis, angle) = \left(\left[\begin{matrix}x\\y\\z\end{matrix}\right],\theta\right) 来描述方向。


 

 
一般来说，轴角表示方向时，会出现4个参数，其中3个用于表示旋转轴，1个用于表示旋转角大小。而如果我们规定了表示旋转轴的向量为单位向量 e ，考虑到 \sqrt{x^2+y^2+z^2}=1 ，我们就可以用两个参数表示出旋转轴，总共只需要三个参数，跟欧拉角一样多。旋转向量我们可以用 \bm{\theta} = \theta e 表示，其中 e 是单位向量。顺便提一句，这里的旋转轴我们称为欧拉轴(Euler axis)，这里的旋转向量我们称为欧拉向量(Euler vector)。是的，全是这个人自己在玩儿。

　　现在我们可以说说四元数了。我们引入四元数是为了更方便地计算轴角表示的方向变换。四元数是什么？四元数是复数，更具体地说四元数是存在三个虚部的复数。q = w + ix + jy +kz ，其中i,j,k是虚数单位，满足 i^2=j^2=k^2 = -1 ，且 i\cdot j=k ， j \cdot i=-k 。为了让大家更直观地明白用四元数运算的优点，我们简单回顾一下高中学的复数运算。

加法：

q_1+q_2 = (w_1 + w_2) + i(x_1+x_2) + j(y_1 + y_2) + k(z_1 + z_2) = [(w_1 + w_2), (v_1 + v_2)]

乘法：

q_1\cdot q_2 = (w_1w_2-x_1x_2-y_1y_2-z_1z_2)+\\i(w_1x_2+x_1w_2+y_1z_2-z_1y_2)+\\j(w_1y_2-x_1z_2+y_1w_2+z_1x_2)+\\k(w_1z_2+x_1y_2-y_1x_2+z_1w_2)

将四元数用于计算轴角表示运算时，我们通常写成向量形式(vector representation) q = [w,\vec{v}] = \left[w,\left(\begin{matrix}x\\y\\z\end{matrix}\right)\right]，为了表达清晰和计算方便，我们将w,x,y,z的取值定位 w^2+x^2+y^2+z^2 = 1 ，并称之为单位四元数，在方向计算时单位四元数中w,x,y,z分饰的角色我们后面会解释。此时，复数乘法可表示为向量形式：

q_1\cdot q_2 = [w_1, \vec{v_1}]\cdot[w_2, \vec{v_2}] = [w_1w_2-v_1v_2,v_1\times v_2 + w_1\cdot v_2+w_2\cdot v_1]

要注意这里出现的向量叉乘没有交换率。

同时，我们也可以将乘法写成矩阵形式，以用于和欧拉角计算作比较：

q_1q_2 = \left[\begin{matrix} w_1&-x_1 & -y_1 & -z_1\\ x_1 & w_1 & -z_1 & y_1\\ y_1 & z_1 & w_1 & -x_1\\ z_1 & -y_1 & x_1 & w_1 \end{matrix}\right]\left[\begin{matrix} w_2\\x_2\\y_2\\z_2 \end{matrix}\right]

观察此式，我们发现两个四元数相乘，需要存储8个单位数据，也就是说，每个参与运算的四元数只要存储4个单位数据 (w,x,y,z)即可。

此外我们还需要几个特殊量和性质：

  • 四元数的模： \|q \| = \sqrt{w^2+x^2+y^2+z^2}
  • 四元数共轭： q^*=(w+ix+jy+kz)^*=w-ix-jy-kz
  • 共轭的向量形式： q^* = ([w, \vec{v}])^* = [w,-\vec{v}]
  • 四元数倒数： q\cdot q^{-1} = q^{-1}\cdot q = 1
  • 共轭与倒数的关系： q^{-1} = \frac{q^*}{w^2+x^2+y^2+z^2} 可见对于单位四元数 q^* = q^{-1}
  • 共轭与倒数的性质： (q_aq_b)^{-1} = q_b^{-1}q_a^{-1} ， (q_aq_b)^* = q_b^*q_a^*
  • 四元数运算同时满足结合律和分配律：

(q_1+q_2)+q_3 = q_1+(q_2+q_3)

(q_1q_2)q_3 = q_1(q_2q_3)

(q_1+q_2)q_3 = q_1q_3+q_2q_3

q_1(q_2+q_3) = q_1q_2+q_1q_3



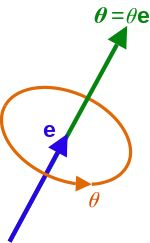
了解了上面的计算法则，我们就可以利用四元数来计算方向变换过程了。还记得我们之前说过计算时四元数我们用向量形式表示，且保证它是单位四元数吗？其实四元数的向量形式我们还可以进一步改写为极形式(polar representation)

q = \|q\|[cos\theta, \vec{n}\cdot sin\theta] ，

其中 \|q\| 代表了四元数的模，单位四元数模为1，而 \theta 是四元数表示的旋转过程的半角大小，也就是说(2\theta) 就是旋转角大小， n 则是表示旋转轴方向的单位向量。用这种表示方法，四元数即可表示任意轴角表达的方向变换。方向变换的计算方法我们这里给出结论，大家可以自己通过计算来验证一下，如有兴趣也可以推导一下过程：

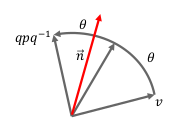
先将原向量坐标表示为四元数 p=[0,\vec{v}] ，将旋转角度及旋转轴表示为单位四元数 q ，旋转后的向量坐标可通过 r = q\cdot p\cdot q^* 或 r = q \cdot p\cdot q^{-1} 计算得出。

至此，四元数算是正式引入完了，下面我们来看看为什么我们要引入四元数。

 

先说结论，四元数的引用是为了减少计算量和计算时存储占用的空间。

但是，如果你足够细心，一定可以发现两个四元数相乘的过程其实是一个4×4矩阵与一个4×1矩阵相乘的过程，而四元数计算一次变换需要两次这个过程，其中包括24次加法运算和32次乘法运算，反观欧拉角的矩阵变换只要进行一次3×3矩阵和3×1矩阵的乘法运算，其中包括6次加法运算和9次乘法运算，运算量明显是四元数更大一些。如果你再细心一些可以发现，四元数运算时虽然有个4×4矩阵参与运算，但是矩阵中的每一项都是已经存储过的单位数据，而参与欧拉角运算的3×3矩阵则要通过另外已存储的单位数据进行的16次乘法运算，4次加法运算以及4次符号改变运算来求出，不过即使加上这些运算过程，矩阵运算也只要25次乘法运算，10次加法运算以及4次符号改变运算，运算量上来说，欧拉角的矩阵运算依然比四元数运算要有优势。

但事实上，我们一般遇到的运动学问题很少会有只做一次方向转换的情况出现，对于复杂的系统和机器人来说，我们往往会面对数量庞大的转变方向过程。这种情况下四元数的优势就体现出来了，我们考虑多次变换的四元数运算：

R = R_1R_2...R_{n-1}R_n=q_n(q_{n-1}...(q_2(q_1\cdot p\cdot q_1^*)q_2^*)...q_{n-1}^*)q_n^* ，

我们利用结合律来看：

R = R_1R_2...R_{n-1}R_n=(q_nq_{n-1}...q_2q_1) p( q_1^*q_2^*...q_{n-1}^*q_n^*) ，

考虑到四元数共轭有性质： (q_aq_b)^* = q_b^*q_a^* ，我们可以把原式改写为

R = R_1R_2...R_{n-1}R_n=(q_nq_{n-1}...q_2q_1) p(q_nq_{n-1}...q_2q_1)^* ，

可以发现，原向量 p 左右两侧括号里的运算结果是一对共轭四元数，也就是说可以利用3次易号运算代替n次四元数相乘运算，大大减少了计算量。反观欧拉角的矩阵计算，虽然一次旋转时，仅仅是3×3矩阵和3×1矩阵的乘法运算，但是对于多次运算来说， M_nM_{n-1}...M_2M_1 的运算却是多个3×3矩阵相乘，与四元数 q_nq_{n-1}...q_2q_1 的每组4×4矩阵与4×1矩阵的相乘相比运算量要大上不少，加上3×3矩阵中多数元素都是需要通过单位数据再次运算才能得到的，更是增加了运算量的需求。总体看来，在复杂的多次变换情况下，四元数比矩阵运算所需要的运算量更小。

另外，我们之前提到过，每一个3×3的矩阵至少需要存储6个单位数据才可以记录，而每个四元数仅需要4个单位数据即可(其实考虑到四元数是单位四元数，在保证w已知的前提下，x,y,z缺少任意一个都是可以通过运算推导出四元数的，也就是说可能只要占用三个数据的存储空间，前提是对x,y,z的定义域要有限制)，在大量变换的运算中，四元数的应用可以节约非常多的存储空间。

 

拥有以上两个优点，加上规避了Ambiguity的问题，我们在表示方向和方向变换时会经常使用四元数的运算。不过四元数也是有缺点的，在复杂运动中，方向旋转和位移往往是同时发生的，在运用欧拉角矩阵运算时，我们考虑平移运算只要改写矩阵为4×4 homogeneous matrix \left[ \begin{matrix} \left[ \begin{matrix} &&\\&R&\\&& \end{matrix}\right]\begin{matrix} x\\y\\z \end{matrix}\\ \begin{matrix} 0&0&0&1 \end{matrix} \end{matrix} \right] 即可，而四元数则必须重新写为 Rot(\vec{n}, \theta) 的形式以找到homogeneous matrix，非常麻烦。

Rot(\vec{n},\theta)=\left[\begin{matrix} n_x^2+(1-n_x^2)c & n_xn_y(1-c)-n_zs & n_xn_z(1-c)+n_ys & 0\\ n_xn_y(1-c)+n_zs & n_y^2+(1-n_y^2)c & n_yn_z(1-c)-n_xs & 0\\ n_xn_z(1-c)-n_ys & n_yn_z(1-c)+n_xs & n_z^2+(1-n_z^2)c & 0\\ 0 & 0 & 0 & 1 \end{matrix}\right] ，其中 c = cos\theta, s = sin\theta

 

 

 
 
参考文献：
https://www.zhihu.com/question/47736315/answer/236808639

www.qiujiawei.com/understanding-quaternions/
posted @ 2019-04-23 21:50  心田居士  阅读(2354)  评论(0)  编辑  收藏  举报