PCA主成分分析方法

PCA： Principal Components Analysis，主成分分析。

1、引入

　　在对任何训练集进行分类和回归处理之前，我们首先都需要提取原始数据的特征，然后将提取出的特征数据输入到相应的模型中。但是当原始数据的维数特别高时，这时我们需要先对数据进行降维处理，然后将降维后的数据输入到模型中。

　　PCA算法是专门用来对高维数据进行降维而设计，通过将高维数据降维后得到的低维数能加快模型的训练速度，并且低维度的特征具有更好的可视化性质。另外，数据的降维会导致一定的信息损失，通常我们可以设置一个损失阀值来控制信息的损失。

　　设原始样本集为：，即样本数为m个，每个样例有n个特征维度。

 

2、预处理

　　在使用PCA降维之前，样本集需要满足两个条件：

　　1）特征去均值化（即均值零化）。对每个特征，使用当前特征的值减去该维特征的平均值。对第i个样例的第j个特征，计算公式为：

　　其中第i个特征的均值为：

　　当处理自然图像时，则将每个特征减去图像本身的均值，而不是减去该特征的均值。即：

　　为何需要去均值？这主要是去除均值对变换的影响，减去均值后数据的信息量没有变化，即数据的区分度（方差）是不变的。如果不去均值，第一主成分，可能会或多或少的与均值相关。^[5]

　　2）归一化处理：将不同特征的数据范围归一化到同一范围中，一般将每个值除以当前维的最大值。

 

3、PCA算法

　　PCA算法的核心思想在于找出数据变化的主方向和次方向，如图3.1所示，向量u1 的方向可以认为是数据的主方向，而u2是次方向。

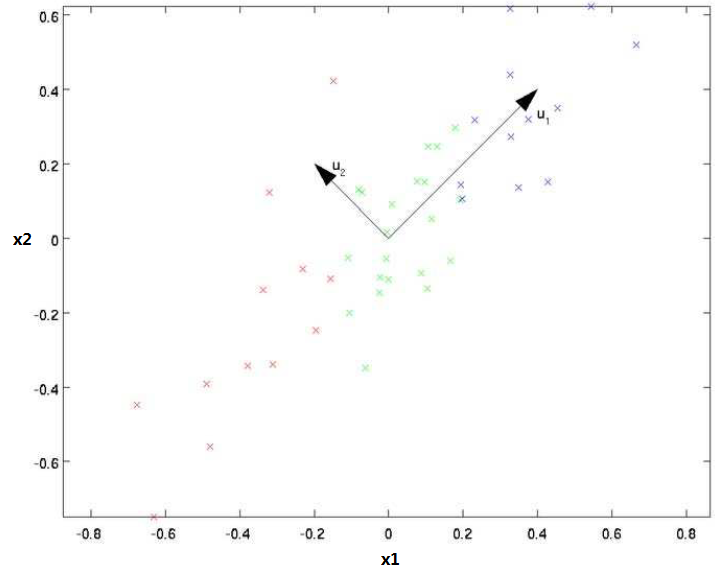
图3.1 数据变化的主次方向^[1]

　　那么如何得到数据变化的主次方向？假设样本集有m个样例，每个样例有n个特征。样本集可以表示为：

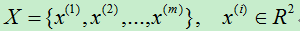
　　第i个样例的特征向量表示为：

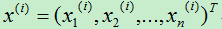
　　则样本集的协方差矩阵为：

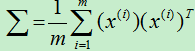
　　协方差矩阵为n*n大小的方阵，具有n个特征向量。

　　其中协方差计算公式为：

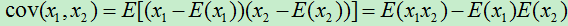
　　计算协方差矩阵的特征向量及对应的特征值。

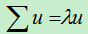
　　将特征向量按特征值的大小按列排放，组成矩阵u=[u1 u2 … un]，对应的特征值由大到小分别为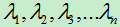：。则特征向量u1为主特征向量（对应的特征值最大），u2为次特征向量，以此类推。

　　对于特征值越大的特征向量，样本集在该方向上的变化越大。对于由特征向量组成的矩阵我们称为特征矩阵，特征矩阵是一个正交矩阵，即满足u^Tu=uu^T=I。

　　关于协方差矩阵的计算，以及其中的一些数学原理，可以参考文献[3,4]。

　　如何理解协方差矩阵的特征向量为数据变化的主次方向，以及特征值越大，其对应的特征向量方向上的数据变化越大？

　　答：使用协方差矩阵计算出来的特征值为其特征向量上的样本集的方差，当方差越大，说明数据集在该特征向量方向上越分散，变化越大，所以该方向就可以用来作为数据集的主方向。

　　另外，特征向量之间相互正交，说明各特征之间相关性最小，基本接近0.

　　独立==>不相关<==>协方差为零

　　至此，我们已经得到了数据变化的主次方向，现在我们需要计算样本在每个特征向量上的长度。对于原始样例x，其在特征向量u1方向上的长度为：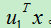

　　现在我们使用特征矩阵来对样本进行旋转：

　　旋转后的坐标变换成了：(u₁, u₂, …, u_n)。

　　现在若要将变换后的数据进行恢复，因为特征矩阵为正交矩阵，所以只需左乘特征矩阵的转置即可：

　　因为：

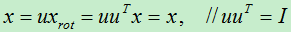
PCA算法过程^[3]：（样本集有m个样例，每个样例n个特征）

1）将原始数据组成一个n*m大小的矩阵。

2）对矩阵的每行进行零均均值化处理，即对每个特征减去该行的均值。

3）计算协方差矩阵，这个过程叫

4）求出协方差矩阵的所有特征向量及对应的特征值。

5）根据特征值从大到小对应的特征向量，取出前k个特征向量组成一个特征矩阵u。

6）将原始数据旋转到特征矩阵u所在的空间中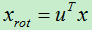，，得到的数据即为降维后的结果。

 

4、损失误差分析

　　在上一步中利用协方差矩阵计算得到n个特征向量，但是我们实际上只使用了前k个特征向量，而将后面的n-k个向量直接近似为0。

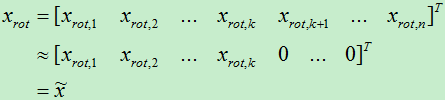
　　直接将后面的特征近似为0会导致一定的损失。K的取值越大，损失的信息就越少，反之损失的信息就会越多。实际上，因为后面近似为0的特征向量对应的特征值是非常的小，故而将后面的特征近似为0不会导致过大的损失。

　　具体损失可以用前k个特征值在所有特征值中所占的比例，由于协方差矩阵的特征值为方差，因而特征值之比即为方差百分比：

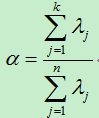
　　其中，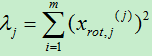

　　在处理图像时，一般需要a>=0.99，而其他情况下一般只需a>=0.95即可。

　　另外，PCA算法具有缩放不变性，即所有的特征分量被放大或缩小相同的倍数，PCA输出的特征向量不会发生变化。

5、白化操作Whitening（白化算法）^[2]

　　白化操作主要用来去除各特征之间的关联度，减少特征冗余。比如图像中相邻像素有一定的关联性，很多信息是冗余的，这时去相关可以采用白化操作。

　　白化操作主要完成两件事情：首先使得不同特征之间的相关性最小，接近0；其次是所有特征的方差相等。

　　常见的白化操作有：

　　1）PCA whitening。在利用PCA得到协方差矩阵的特征向量后，取前k个特征向量，各特征向量相互正交，此时相关性最小；再将新数据（旋转后的数据）的每一维除以标准差即得到每一维的方差为1。方差归一化：

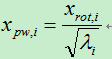
　　pw: PCA white。

　　2）ZCA whitening。首先利用协方差矩阵计算出所有的特征向量后，将所有特征向量取出，再进行方差的归一化操作，最后左乘特征矩阵u（其实相当于把数据还原回去）。

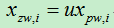
　　它并不降低数据维度，而仅仅在PCA白化的步骤中保留所有成分，最后增加了一个旋转的步骤，这样仍然是单位方差。

 

 

6、总结

　　PCA算法非常巧妙地利用协方差矩阵来计算出样本集在不同方向上的分散程度，利用方差最大的方向作为样本集的主方向。其主要过程是：首先利用样本集及特征构建一个样本矩阵，然后利用样本矩阵计算得到协方差矩阵，再计算协方差矩阵的特征值和特征向量，保留特征值前k大的特征向量作为新的维度方向。再将原始样本数据转换到新的空间维度。

        

 

 

参考文献：

[1] peghoty, http://blog.csdn.net/itplus/article/details/11451327

[2] tornadomeet, http://www.cnblogs.com/tornadomeet/archive/2013/03/21/2973231.html

[3] CodingLabs, http://blog.codinglabs.org/articles/pca-tutorial.html

[4] peghoty, http://blog.csdn.net/itplus/article/details/11452743

[5] viewcode, http://blog.csdn.net/viewcode/article/details/8789524