凸优化
凸优化
由于在SVM等各种地方都会用凸优化来解决问题,所以本篇博客将系统的介绍凸优化如何做,以及一些常见的问题。
基本概念
仿射集(Affine Set)
定义:通过集合C中任意两个不同点的直线仍然在集合C内,则称集合C为仿射集.
\(\forall x_{1},x_{2} \in C, \forall \theta \in R, 则x = \theta * x_{1} + (1 - \theta) * x_{2} \in C\)
凸集
定义:集合C内任意两点间的线段均在集合C内,则成集合C为凸集。
\(\forall x_{1},x_{2} \in C, \forall \theta \in [0, 1], 则x = \theta * x_{1} + (1 - \theta) * x_{2} \in C\)
由于仿射集的条件比凸集的条件要强一些,所以仿射集一定是凸集。
保凸性运算
- 集合交运算;
- 仿射变换:f = Ax + b的形式;
- 透视变换;
- 投射变换
凸函数
定义:若函数f的定义域domf为凸集,且满足\(\forall x, y \in fom f, 0 <= \theta <= 1, 有f(\theta x + (1 - \theta)y) <= \theta f(x) + (1 - \theta)f(x)\)
-
一阶可微
若f一阶可微,则函数f为凸函数当且仅当f的定义域为凸集,且\(\forall x,y \in domf, f(y) \ge f(x) + \nabla f(x)^{T}(y-x)\).
所以,对于凸函数,其一阶Taylor近似本质上是该函数的全局下估计。 -
二阶可微
若函数f二阶可微,则函数f为凸函数当且仅当dom为凸集,且\(\nabla ^{2}f(x) \ge 0\).
常用的凸函数
- 指数函数 \(f(x) = e^{ax}\);
- 幂函数 \(f(x) = x^{a}, x \in R^{+}, a \ge 1 或 a \le 0\);
- 负对数函数 \(f(x) = -lnx\);
- 负熵函数 \(f(x) = xlnx\);
- 范数函数 \(f(x) = \lVert x \rVert\);
- 最大值函数 \(f(x) = max(x1, x2, x3, .... ,xn)\);
- 指数线性函数 \(f(x) = log(e^{x1} + e^{x2} + ... + e^{xn})\)
Jensen不等式
- \(f(\theta x + (1 - \theta)y) \le \theta f(x) + (1 - \theta)f(y)\)
- 扩展到连续形式:
- 若\(p(x) \ge 0 on S \subseteq dom f, \int_{S}p(x)dx = 1\), 则\(f(\int_{S}p(x)xdx) \le \int_{S}f(x)p(x)dx\),进一步可以得出:\(f(Ex) \le Ef(x)\)
共轭函数
原函数\(f : R^{n} \to R\)共轭函数定义:
\(f^{*}(y) = sup_{x\in dom f}(y^{T}x - f(x))\)
显然,定义式的右端是关于y的仿射函数,对它们逐点求上确界,得到的函数\(f^{*}(y)\)一定是凸函数。
凸函数的共轭函数的共轭函数是其本身。
凸优化
对偶函数
-
优化问题的基本形式:

其中,\(f_{i}(x)\)为凸函数,\(h_{j}(x)\)为仿射函数 -
将上述优化问题写成Lagrange乘子法的形式:
\(L(x, \lambda, \nu) = f_{0}(x) + \sum_{i=1}^{m}\lambda_{i}f_{i}(x) + \sum_{j=1}^{p}\nu_{j}h_{j}(x)\)
对固定的x,Lagrange函数\(L(x, \lambda, \nu)\)为关于\(\lambda\)和\(\nu\)的仿射函数。
其中,\(\lambda \ge 0\) & \(\nu \in R\). -
Lagrange对偶函数(dual function):
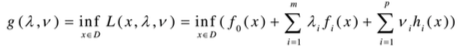
显然,若原问题有最优值\(p^{*}\),则\(g(\lambda, \nu) \le p^{*}\),即Lagrange对偶函数是凹函数。
我们用Lagrange对偶函数来求解原问题的最小值最优解。那么,为什么可以这样做呢?思考下面的鞍点解释。
鞍点解释
接下来,我们先将优化问题放下,看看原优化问题与Lagrange对偶函数的优化问题有什么关系。
- 原问题是:\(inf_{x} f_{0}(x)\);
- 换一个写法:\(inf_{x}sup_{\lambda \ge 0}L(x, \lambda)\)
- 而Lagrange对偶问题,是求对偶函数的最大值:\(sup_{\lambda \ge 0}inf_{x}L(x, \lambda)\)
- 我们有:\(sup_{\lambda \ge 0}inf_{x}L(x, \lambda) \le inf_{x}sup_{\lambda \ge 0}L(x, \lambda)\)
证明:\(max_{x}min_{y}f(x, y) \le min_{y}max_{x}f(x, y)\)

强对偶KKT条件
有了上面的解释,但其实若要对偶函数的最大值即为原问题的最小值,需要满足Karush-Kuhn-Tucker(KKT)条件:

这部分的应用在SVM中也有体现,关于SVM详解,请看我的这篇博客。
至此,关于凸优化中应该掌握的地方已经列好了。总体而言,解决凸优化问题,首先我们要保证待解决的问题是满足凸优化的条件的,然后我们用Lagrange乘子法来解决该问题。如果难以解决,则使用其对偶形式,注意需要满足KKT条件。
总结
本篇博客主要分析了凸函数的优化问题怎样通过Lagrange对偶函数来求解,步骤如下:
- 我们的目标是求原函数\(min_{x}f(x)\),同时它有很多限制条件;
- Lagrange乘子法:\(L(x, \lambda, \nu) = min_{[x, \lambda, \nu]}f(x) + \lambda f_{i}(x) + \nu h(x)\);
- Lagrange对偶函数(求关于x在定义域上的下确界):\(g(\lambda, \nu) = inf_{x \in D}L(x, \lambda, \nu)\);
- 对Lagrange对偶函数求最大值来近似原函数的最小值:\(max_{\lambda, \nu}g(\lambda, \nu)\),同时\(max_{\lambda, \nu}g(\lambda, \nu) \le min_{x \in D}f(x)\)成立(见鞍点解释)。


