状态机:如何构建稳定的婚姻
相关:
在这篇博文中我会依次复习一下状态机的定义、不变性原理、部分正确性和可终结性这四个和状态机相关的知识,并举出一些有意思的例子辅以说明,最后解决一个关于稳定婚姻的有趣问题。
0. 什么是状态机
状态机是对“step-by-step“过程的一种抽象模型。
由于计算机程序本身就是一种确定的”step-by-step“过程,所以状态机在计算机科学领域用的很普遍。其中最重要的一个用途就是证明在程序运行的过程中某一些属性能够确定被保持,这些属性也被称为”不变量“。在实际生活中有很多”不变量“,例如飞机自动飞行的过程中要保证高度值不能低于1KM,或者核电站在运行的过程中内芯温度不能高于1K摄氏度等等。
1. 状态机的状态与转换
从集合论的角度来看,状态机就是将一个二维关系映射到一个集合上——这个集合的元素叫做”状态“,他们之间的关系称为”转换“,p转换为q写为p -> q。一个状态机的所有可能转换被称为转换图,每一个状态机都有一个设计的”起始状态“。
下面举一个简单的例子,有一个从0到99的累加器,当累加器的状态达到99后再进行累加就会发生溢出:
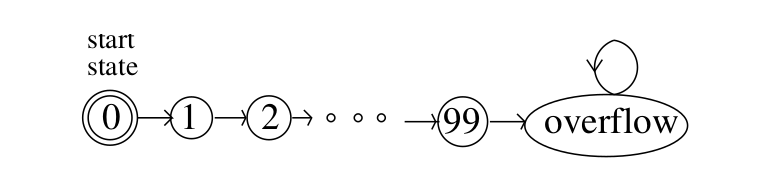
将这个累加器用公式表示就是:

如果一个状态机的状态是有限的,我们就称其为有限状态机,例如上面这个例子。相反,如果状态有无穷多个,我们就称其为无限状态机,如果上面这个累加器不设置溢出的话就会变成一个无线状态机。在实际使用时,转太极的状态转换可能会有一些输入输出,转换时对不同的状态也会有不同的花费或者几率,这篇博文中不考虑这些因素。
2. 不变性原理
如果一个状态能够在状态机的某次执行中出现,我们就称之为”可到达的“。如果P是一个状态机的不变量,那么无论何时P(n)成立,当状态n -> r后,P(r)也成立。特别地,如果对于一个状态机的起始状态P(n)成立,那么对于任何可到达的状态r,P(r)都成立。
可以看出,不变性原理就是适用于状态机的归纳法 ——如果某个谓语在一开始成立,那么就推出在接下来的所有步骤中它均成立。
下面举一个例子,在《虎胆龙威3》这部电影中,恐怖分子在一个喷泉旁放置了炸弹,并提供了一个5加仑的桶和一个3加仑的桶,如果拆弹人员能够利用这两个桶准确的得到4加仑的水并放在一旁的秤上,炸弹就不会爆炸。


这个问题看起来也不难,一个小学生也能马上想出来,例如这样一个解法:将3加仑桶装满,全部倒入5加仑桶中,然后再将3加仑装满,倒入5加仑桶中直到5加仑桶满,然后倒掉5加仑桶里的水。这时3加仑桶里有1加仑水,将这1加仑的水倒入刚刚清空的5加仑桶中,然后装满3加仑桶并全部倒入5加仑桶中,这时5加仑桶中的水就是4加仑了。
那么,对于任何两个容积的水桶这个问题都是有解的吗?如果我们将5加仑的水桶换成9加仑的水桶,还能拆除炸弹吗?显然是不行的,因为我们每次的操作都只能是3的整数倍,所以结果也一定是3的整数倍,也就不可能得到4这个结果了。下面我们利用不变性原理来证明这一点:
首先我们建立一个状态机,它的状态表示为(b, l),其中b代表big jug,l代表little jug,所以0 <= b <= 9, 0 <= l <= 3且b、l均为整数。该状态机的起始状态为(0, 0),对于关系的转换,有以下6种可能:
- 装满小水桶:(b, l) -> (b, 3)
- 装满大水桶:(b, l) -> (9, l)
- 清空小水桶:(b, l) -> (b, 0)
- 清空大水桶:(b, l) -> (0, l)
- 将小水桶里的水倒入大水桶中。(1) 如果b + l <= 9,(b, l) -> (b+l, 0). (2)否则,(b, l) -> (9, l - (9-b))
- 将大水桶里的水倒入小水桶中。(1) 如果b + l <= 3, (b, l) -> (0, b+l). (2)否则,(b, l) -> (b - (3-l), 3)
注意到这个状态机和我们之前那个计数器状态机不同,它每一次的状态转换的选择不止一个,像这样的状态机就称为”非确定性的“(nondeterministic),计数器状态机则称为”确定性的“(deterministic)。
设P((b, l))为“b,l均为3的整数倍”,下面我们证明它是对状态机所有状态都成立的不变量:
首先证明如果P(q)成立,q -> r,那么P(r)也成立:
- “装满操作”,得到(9, l)或者(b, 3),由于9, 3, l, b都是3的整数倍,命题成立
- “清空操作”,得到(0, l)或者(b, 0),由于0, l, b都是3的整数倍,命题成立
- 将小水桶里的水倒入大水桶中。(1) 如果b + l <= 9,(b, l) -> (b+l, 0) 由于b+l, 0都是3的整数倍,命题成立 (2)否则,(b, l) -> (9, l - (9-b)) 由于9, l - (9-b)都是3的整数倍,命题成立。
- 将大水桶里的水倒入小水桶中。(1) 如果b + l <= 3, (b, l) -> (0, b+l) 由于0, b+l都是3的整数倍,命题成立 (2)否则,(b, l) -> (b - (3-l), 3) 由于b - (3-l), 3都是3的整数倍,命题成立。
综上,P是该状态机的一个不变量。又因P(0, 0)也成立,而(0, 0)是该状态机的起始状态,由不变性原理,P对于该状态机所有可到达的状态都成立。因为4不是3的整数,所以我们不可能得到一个装有4加仑水的桶。证毕。
3. 状态机的部分正确性和可终结性
我们可以从两个方面判定程序(状态机)是否可用:部分正确性(partial correctness)和可终结性(termination)。部分正确性并不是指程序结果是部分正确的,而是因为程序在计算“部分关系”(partial relation)的时候可能不会终止,所以这个正确性是“部分的”,或者这么说,如果程序最终停止,得出的结论一定是正确的。可终结性则是指程序理论上是会最终停止的。
通常情况下,部分正确性可以用不变性原理证明,而可终结性可以用良序原理证明。下面我们用一个常见的快速求幂算法来解释这两个性质,对于求a^b的值,算法如下:

首先建立起这个状态机:其的状态为(x, y, z),所以其起始状态为(a, 1, b),状态转换为:(1) 如果z != 0 && z为偶数,(x, y, z) -> (x^2, y, z/2) (2) 如果z != 0 && z为奇数,(x, y, z) -> (x^2, xy, z/2)。
接着证明该状态机的不变量P((x, y, z)):z为自然数且y*(x^z) = a^b。设P((x, y, z))成立;则在第一种转换下,z为自然数,y*((x2)(z/2)) = ab。在第二种转换下,z为自然数,y*x*((x2)^(z/2))(z除2后舍去了余数1)= a^b。得证,又因为起始状态P((a, 1, b))依然成立,由不变性原理我们便证明了该程序/状态机的部分正确性。
在证明该程序的可终结性之前,先介绍一下“派生变量”(Derived Variables)这个概念:
我们在证明程序是可终止的时候通常会使用程序中的一个非负数值,如果它在程序每一步的运行中都是严格递减的,由良序原理,它不可能无限递减,最终会达到那个最小值,也就是程序终止。如果更普遍的理解,我们将一套设计好的操作f作用于状态p,称之为f(p),如果f(p)是严格递减的,即(p -> q) implies f(q) < f(p),且对于所有可到达状态,f(p)构成一个良序集合,那么就可以得到该程序/状态机是可终止的(f类似于物理学里面的势能函数)。
另外,这种方法也常常用于算法的分析,即对于一个算法生成一个派生变量,在算法运行的过程中观察这个变量的变化。
对于上面例子中的算法,我们可以令派生变量f((x, y, z)) = z,我们已经证明了z是自然数(即良序集合),且当z不为0时z/2 < z即f((x, y, z)) > f((x', y', z')),所以可以得出该程序是可终止的。
综上,我们证明了该算法具有可终止性和部分正确性。
4. 稳定婚姻问题
假设你是一位媒人,现在男人和女人的数量一样,每一个男人按照他的标准在心中给所有的女人排一个名单次序,女人也一样,这个配偶名单不一定是对称的,也就是说,如果小明最希望小红称为他的妻子,小红可能最希望小刚成为她的丈夫。这里不考虑同性恋的问题,你的任务就是找到一种匹配的方法,让每个人都找到自己的配偶,并且所有的婚姻都是稳定的 ,即不存在两个不是配偶的人互相喜欢胜过各自的配偶。举一个不稳定婚姻的例子:
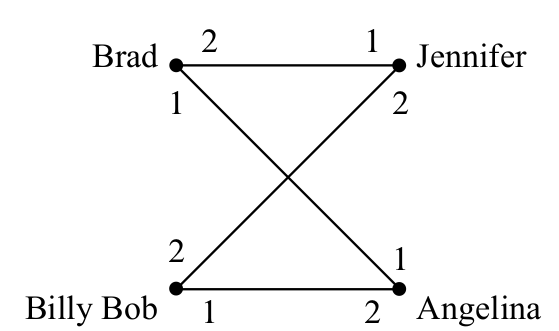
如果我们将Brad和Jennifer配对,Billy Bob和Angelina配对,那么Brad喜欢Angelina胜过自己的配偶Jennifer(1 < 2),而Angelina也喜欢Brad胜过自己的配偶Billy Bob,这就形成了一个不稳定的婚姻:Brad和Angelina可能会在晚上一起悄悄的做数学作业!与此相反,如果我们将如果我们将Brad和Angelina配对,Billy Bob和Jennifer配对,虽然Billy Bob和Jennifer可能会有些不高兴,但是婚姻将会是稳定的——即使Jennifer去勾引Brad,Brad还是会深爱着Angelina的;)Billy Bob也无法让Angelina对自己感兴趣。
上面是一个4个人的例子,如果给你2n个人和他们的理想配偶名单(对所有异性的好感度),你还能设计出一个配对方法吗?
事实上,无论是对少个人,只要不存在同性婚姻,都会有一种稳定婚姻的配对方法——而且这种方法非常简单和易懂:
- 首先每一个男人去向他名单上最靠前的女士示爱,示爱后他即成为该名女士的候选者。
- 随后每一个女人从她所有的候选者里选出她最喜欢的男士对他说“我们可能结婚,请不要将我从你的名单划掉”,并对其他的男人说“我对你不感兴趣,回家做数学作业去吧!”。
- 示爱被拒绝的男人他的名单中将拒绝她的女士划掉。
- 当每一个女人都有且仅有一个候选人时,配对完成。否则跳转到第一步。
我们需要证明这个算法具有以下性质:
- 该算法最终会结束。(可终结性)
- 结束时每一个人都会结婚。
- 结婚后婚姻是稳定的。(这两条是部分正确性)
为了便于分析,我们将这个过程建立为一个状态机——每次的状态为每个男人和该轮次他会去示爱的女士,即他名单的首位女士。
1.该算法最终会结束:
设派生变量f(x) = 每个男人名单上留下的女士数量之和,一开始f(x) = n^2。每次循环时f(x)都会减少——因为这意味着至少有一名女士被两个男士示爱了,所以循环才不会终止,被拒绝的男士也会将她从名单上划去。又因为不会有女士新增到男士的名单上,所以f(x)在该状态机转换过程中是单调递减的。又因为f(x) >= n(终止时情况),所以f(x)的取值在一个良序集合中,得到该状态机是可终止的。
2.1结束时每一个人都会结婚:
可以观察到,对于一名女士而言,如果她这一轮次将Frank留了下来,Frank就不会将她从他的名单上划去,第二天Frank依然会来找她示爱。如果第二天该名女士遇到了她更喜欢的男人,她才会赶走Frank,所以说,女士的候选者只会“越来越好”。这好像是一个不变量:设P(w, m)为男士w将m从他的名单中划去,那么m一定有了更好的候选人。由于P(w, m)对于一开始也成立,由不变性原理P对所有的状态都成立。
反证法,如果结束的时候有一个男士Bob没法结婚,即他的名单上所有的女性都拒绝了他(他的名单为空了),那么由于P对所有状态成立,所有的女性都有一个比Bob更好的候选人,由于男人和女人的数量是一样的,所以这是不成立的,因此结束时每一个人都会结婚。
2.2结婚后婚姻是稳定的:
我们可以证明匹配完成后不存在可能有暧昧关系的两个人。假设匹配完成后Jen和Brad两个人不是配偶,那么根据Brad的名单会有以下两种情况:
Case 1: Brad名单上已经没有Jen了,即他向Jen示爱过并被拒绝了。由上面的不变量P,Jen一定有一个比Brad更加喜欢候选人并和他结了婚,所以Jen不会被Brad吸引,即他们不会有暧昧关系。
Case 2: Jen还在Brad的名单上,由于Brad是按照好感顺序去示爱的,如果最后Jen还在他的名单上,Jen又没有和他结婚,那么Brad一定和一个他更有好感的女人结了婚,所以Brad不会在意Jen的“勾引”,也就不会和她有暧昧关系。
由于Brad和Jen的选择是随机的,所以匹配后任何人之间不会产生暧昧关系,即婚姻一定是稳定的。
这个方法对男人有利还是女人有利?
你可能觉得女人具有选择权——她们每天都能选择一个更好的配偶,男人只能被拒绝——只能选择越来越差的配偶,但实际上在该算法中女人是很弱势的一方!我们前面只证明了婚姻匹配方法得出来的匹配的正确性,事实上,稳定的匹配方法可能不止一种,例如,如果我们还是利用婚姻匹配算法,将匹配时的男女属性换一下就可能得到不同的结果(还是稳定的)。
称一个人对于另一个人是“可行配偶”如果在某一个的稳定匹配中他们可以成为夫妻。下面证明上面算法的状态机具有一个不变量Q:对于女人w和男人m,如果w被m从名单中划掉了,那么w对于m不可能是“可行配偶”。
反证法,假设某个时候Alice要被Bob从名单中划去因为Alice选择了另一位叫Frank的男性,如果Alice和Bob成为了配偶,那么Frank也就只能划掉Alice选择更“差”的一位女性,而Alice也就只能跟着不那么喜欢的Bob,所以Frank和Alice之间就可能发生暧昧关系,因此Alice和Bob不可能是可行配偶。
称在一个人所有的”可行配偶“中Ta最喜欢的那一个为”最理想配偶“,最不理想的那一个为”最不理想配偶“。下面证明如果使用上面的婚姻匹配算法,男人们总会娶到”最理想老婆“,而女人们总会娶到”最不理想老公“。
证明:如果Bob利用上面的算法和Alice结了婚,那么之前在名单中Alice之上的女性都被Bob划掉了,由不变性Q,被划掉的女性都不是”可行配偶“,而Alice又是划掉操作后最排行最高的女性,所以Alice是Bob的”最理想配偶“。另一方面,如果Alice对她的丈夫好感度低于对Bob的,那么Bob一定取了一位不是”最理想配偶“的人,这样Alice和Bob就可能发展暧昧关系,所以Bob一定是Alice的”最不理想配偶,证毕。
婚姻匹配算法的实际应用:
- 在50年代的时候,美国启动了一项名为国家公民匹配(National Resident Matching Program,NRMP)的计划,该计划主要是为了解决从学校毕业的学医学生和医院之间的匹配关系——尽量使学生和医院都满意,在该计划中就大量使用到了婚姻匹配算法,即医院和学生分别充当男人和女人。其发明人Shapley获得了2012年的诺贝尔经济学奖。
- 大量的交友网站使用到了该算法(当然男人不会向女人去示爱,都是计算机完成的)。
- 《Mathematics for Computer Science 》的作者之一Tom Leighton创立了互联网接口公司Akamai, 他们将婚姻匹配算法用到了服务器和用户的资源调配之中(CDN)。其中网络请求(客户)作为女人,网站服务器作为男人;网络请求对服务器的“好感度”取决于延迟和丢包率,网站服务器对于网络请求的“好感度” 取决于连接带宽和主机代管商的成本。
参考:


