Leetcode | Largest Rectangle in Histogram

Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

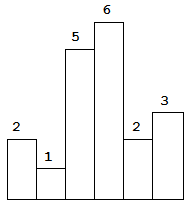
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

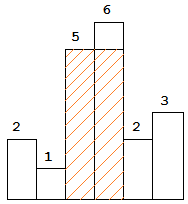
The largest rectangle is shown in the shaded area, which has area = 10 unit.

For example,
Given height = [2,1,5,6,2,3],
return 10.

做不出来。完全的O(n^2)过不了。看了水中的鱼的解法，自己再把这两种算法重写了一次。

Method I

brute force+剪枝。O(n^2)。只有当前值比下一个值大的时候，才有必要往回计算它的面积。比如图中的height[2]=5，height[3]=6。假设height[2]往回找到一个区间[i...2]面积最大，那么一定会有一个[i...3]的面积比它还大。所以只需要从height[3]往回找就行了。

class Solution {
public:
    int largestRectangleArea(vector<int> &height) {
        int n = height.size();
        if (n == 0) return 0;
        
        int max = 0, min, area;
        
        for (int i = 0; i < n; ++i) {
            if (i < n - 1 && height[i] <= height[i + 1]) continue;
            
            min = height[i];
            for (int j = i; j >= 0; --j) {
                if (height[j] < min) min = height[j];
                area = min * (i - j + 1);
                if (area > max) max = area;
            }
        }
        
        return max;
    }
};

Method II

用一个栈来实现。其实也是灵感来自于Method I。 对于一个呈上升趋势的多个点，只有最高的点需要往回扩展。假设height[i]>height[i+1]，那么我们从i往回扩展，扩展到什么位置呢？

假设我们扩展到height[j]<=height[i+1]，找到面积最大，那么我们一定能找到[j...i+1]比[j...i]的面积更大（高都为height[j]，宽度[j...+1]更大）。

为了记录这个宽度，我们在stack中push的是index。这个算法有点类似于Longest Valid Parentheses.

这个j怎么求呢？ 因为栈中元素是递增的，并且栈中元素的下标其实就对应于可以扩展的区间。height[i]>height[i+1]。对于栈中的元素，如果stack不为空，那么从stack中pop出height[i]后，[stack.top()+1...i-1]这一段就是可以扩展的区间。如果为空，那么说明[0...i-1]都是可以扩展的。

class Solution {
public:
    int largestRectangleArea(vector<int> &height) {
        int n = height.size();
        if (n == 0) return 0;
        
        int max = 0, last, area;
        
        stack<int> indexes;
        height.push_back(0);
        
        for (int i = 0; i < height.size(); ) {
            if (indexes.empty() || (height[i]>=height[indexes.top()])) {
                indexes.push(i);
                i++;
            } else {
                while (!indexes.empty() && height[indexes.top()] > height[i]) {
                    last = height[indexes.top()];
                    indexes.pop();
                    area = last * (indexes.empty() ? i : i - indexes.top() - 1);
                    if (area > max) max = area;
                }
            }
        }
        
        return max;
    }
};

Line 10 push一个0是为了处理最后栈不为空的情况。

注意Line 21之后并没有i++，这是为了继续处理height[i]。

内循环是出栈，因为栈最大只可能为n，同时也不能重复入栈，所以整个时间复杂度为O(2*n)，空间复杂度为栈大小O(n)。

水中的鱼提供了一个更简洁的实现代码。主要是将出栈的代码分摊到循环中了。于是我也重新实现一遍。

class Solution {
public:
    int largestRectangleArea(vector<int> &height) {
        int n = height.size();
        if (n == 0) return 0;
        
        int max = 0, last, area;
        
        stack<int> indexes;
        height.push_back(0);
        
        for (int i = 0; i < height.size(); ) {
            if (indexes.empty() || (height[i]>=height[indexes.top()])) {
                indexes.push(i);
                i++;
            } else {
                last = height[indexes.top()];
                indexes.pop();
                area = last * (indexes.empty() ? i : i - indexes.top() - 1);
                if (area > max) max = area;
            }
        }
        
        return max;
    }
};

 

事后诸葛：

如果可以找到一个区间，这个区间符合一定的出栈入栈规律，就可以像此题或者Longest Valid Parentheses用一个栈来定位区间。