博客作业06--图
1.学习总结(2分)
1.1图的思维导图
1.2 图结构学习体会
- 深度遍历算法：
常用递归方法实现 - 广度遍历算法：
借助队列实现
总的来说，这两个遍历相对后面的算法相对简单些 - Prim和Krukcal算法：
用于求最小生成树
两者方法各有各的特点，prim算法用lowcost数组存放最小的路是很巧妙地算法，而kruscal算法则是按从小到大的顺序取权值。 - Dijkstra算法：
用于找最短路径。但是不适合含有负权值的带权图求最短路径。 - 拓扑排序算法：
任何一个无环有向图,其全部顶点都可以排成一个拓扑序列。感觉拓扑排序理解起来简单，但是看代码还是不太明白。
总的来说，除了遍历算法，其他算法可能只是大概理解他的原理，对代码的书写还是不太行，还是得看着书写。
2.PTA实验作业（4分）
2.1 题目1：图着色问题
2.2 设计思路（伪代码或流程图）
int main()
{
定义图 g;
int n,e,k;//顶点数，边数，颜色数
输入顶点数，边数，颜色数
CreateMGraph(g,n,e);//建图
int m,b;//方案个数
输入方案个数
for i=0 to m
初始化存放颜色的数组
for j=1 to n {
输入颜色序号
将存有颜色序号的数组插入容器
}
如果 输入颜色个数不为k或者调用check函数发现有重色
输出"No"
else 调用check函数发现没有重色 输出"Yes"
}
}
int check(MGraph g){
for i=1 to g.n {
for j=1 to g.n {
if(g.edges[i][j]==1（有边）&&a[i]==a[j]（重色）)
返回0
}
}
返回 1；
}
2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）
2.4 PTA提交列表说明。
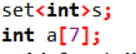一个问题是建栈的位置放在后面导致段错误（原因也不太清楚，和定义a数组顺序调换就对了），
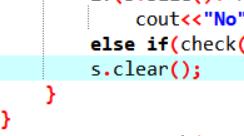还有一个是没注意把clear函数放在括号外了，导致答案错误
2.1 题目2： 修建道路
2.2 设计思路（伪代码或流程图）
定义整型变量q记录道路数,n为村庄的数目,flag表示村庄之间的距离;
定义a,b表示村庄的编号;
for i=1 to i=n
for j=1 to j=n
输入两个村庄之间的距离,用二维数组构建图;
for i=1 to i=Q
输入a,b;
将a,b两个村庄之间的距离改为1;
输出需要新建的路径长度min(n)-q;
2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）
2.4 PTA提交列表说明。
这题一开始不知道怎么解决区分已有路和新建路的问题，后来请教同学知道用1表示已有路径长度，部分正确是因为没有把两个端点相反顺序数组都置为1，修改后答案正确。
2.1 题目3：旅游规划
2.2 设计思路（伪代码或流程图）
Dijkstra函数：
在原有的Dijkstra算法上进行修改
增加一个money数组存储价格，dist数组用来存储距离
money数组初始化为初始点与每个节点的价格
在修改最短路径时
如果发现有更短的路径
则对money数组进行修正，即money[j]=money[u]+edges[u][j].price;
如果路径距离相同的话价格较低
则修正dist数组与money数组
修改前驱即path进行修改
2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）
2.4 PTA提交列表说明。
这题主要是听周同学上课讲的写出来的，原来没什么思路，但是写出来还是出了一些问题。一个是粗心==写成=导致参考数字过了结果部分正确，还有个就是漏了判断条件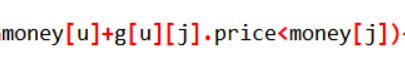
3.截图本周题目集的PTA最后排名（3分）
本次题目集总分：310分
3.1 PTA排名（截图带自己名字的排名）
3.2 我的总分：255分
4. 阅读代码（必做，1分）
#include<stdio.h>
#include<string.h>
#include<queue>
#define N 210
#define M 2010
#define INF 0x3f3f3f3f//定义无穷大
using namespace std;
int dis[N],vis[N],head[N],n,m,edgenum;
struct node{
int from,to,cost,next;
}edge[M];
void init(){
edgenum=0;
memset(head,-1,sizeof(head));
}
void add(int u,int v,int w){
node E={u,v,w,head[u]};
edge[edgenum]=E;
head[u]=edgenum++;
}
void spfa(int beg,int end){//SPFA算法核心
queue<int>q;
q.push(beg);//将起点加入队列
memset(vis,0,sizeof(vis));//用来标记是否在队列中
memset(dis,INF,sizeof(dis));
vis[beg]=1;
dis[beg]=0;
while(!q.empty()){
int u=q.front();
q.pop();
vis[u]=0;
int i;
for(i=head[u];i!=-1;i=edge[i].next){//遍历起点为U的所有的边。
int v=edge[i].to;
if(dis[v]>dis[u]+edge[i].cost){//更新点的最短路
dis[v]=dis[u]+edge[i].cost;
if(!vis[v]){
vis[v]=1;
q.push(v);
}
}
}
}
if(dis[end]==INF)
printf("-1\n");
else
printf("%d\n",dis[end]);
}
int main(){
while(scanf("%d%d",&n,&m)!=EOF&&n!=0&&m!=0){
init();//需要初始化邻接表的表头。
while(m--){
int a,b,cost;
scanf("%d%d%d",&a,&b,&cost);
add(a,b,cost);//对图进行输入，由于是无向图，所以正反两次输入，不用判断重边。
add(b,a,cost);
}
int beg,end;
scanf("%d%d",&beg,&end);
spfa(beg,end);
}
return 0;
-
spfa算法也是一种求最短路径的算法，用了队列和邻接表来实现，他的一个优点是相比Dijkstra算法他的权值可正可负，但是如果是负权值的话需要判断一下是否有负环存在。百度了一下负环的定义：点与点之间相互连接构成一个环，并且该环的总权值为负，那么这就是一个负环。（标记）
-
算法理解：建立一个队列q，初始时队列里只有一个起始点，在建立一个数组dis记录起始点到所有点的最短路径，并且初始化这个数组。然后进行松弛操作，用队列里面的点去刷新起始点到所有点的最短路，如果刷新成功且刷新点不再队列中则把该点加入到队列最后，重复执行直到队列为空。如果存在负环的话，需要建立一个数组来判断每个点进入队列了多少次，否则队列一直都不为空。
