[leetcode]Edit Distance
先给一个例子,两个字符串eeba和abca相似度是多少呢,edit distance是一个很好的度量,定义从字符串a变到字符串b,所需要的最少的操作步骤(插入,删除,更改)为两个字符串之间的编辑距离。
对于eeba,abca它们之间的编辑距离为3,可以按照上面的操作步骤(不是唯一的)将eeba变到abca,1.将e变为a 2.删除e 3.添加c 共3个步骤。
典型的动态规划问题。
EDIT[i,j]表示对于字符串a从1到i的子串和字符串b从1到j的字串的编辑距离。(字符串下标从1开始)
EDIT[i - 1,j] + 1表示对a 在i 位置删除delete操作
EDIT[i,j - 1] + 1 表示insert添加操作
EDIT[i-1, j - 1] + f(x[i],y[j])这里如果x[i] == y[j] 则 f(x[i],y[j]) == 0 否则 ==1
表示不变或者是modify操作。
如果需要记录编辑过程如第一幅图所示,需要用二维数组记录下动态规划过程的路径信息,即记录下前一步骤的位置索引信息。
如下图
class Solution { public: int minDistance(string word1, string word2) { // Start typing your C/C++ solution below // DO NOT write int main() function int row = word1.length() + 1; int col = word2.length() + 1; vector<vector<int> > f(row, vector<int>(col)); for (int i = 0; i < row; i++) f[i][0] = i; for (int i = 0; i < col; i++) f[0][i] = i; for (int i = 1; i < row; i++) for (int j = 1; j < col; j++){ if (word1[i-1] == word2[j-1]) f[i][j] = f[i-1][j-1]; else f[i][j] = f[i-1][j-1] + 1; f[i][j] = min(f[i][j], min(f[i-1][j]+1, f[i][j-1]+1)); } return f[row-1][col-1]; } };



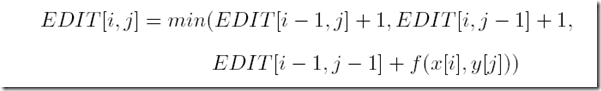



 浙公网安备 33010602011771号
浙公网安备 33010602011771号