coursera普林斯顿算法课part1里Programming Assignment 2最后的extra challenge
先附上challenge要求:
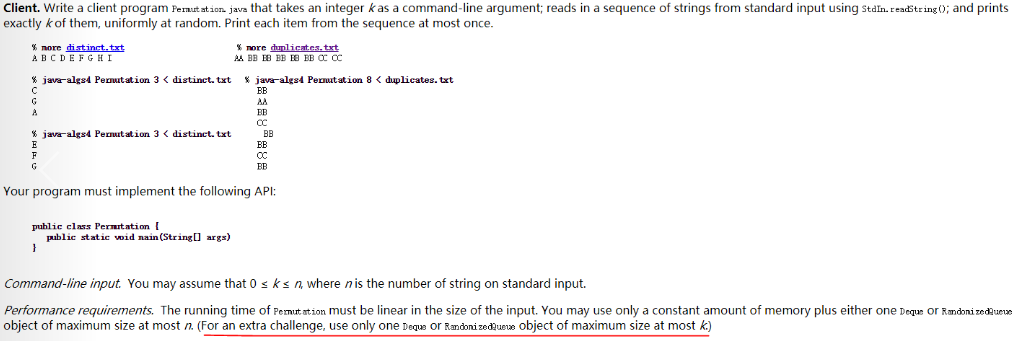
博主最近在刷coursera普林斯顿大学算法课part1部分的作业,Programming Assignment2最后的这个extra challenge当初想了一段时间。最开始的想法就是创建一个RandomizedQueue对象,然后先让前k个String入队,后面的每读一个String以一定概率让它入队,不过之前需要让RandomizedQueue出队一个String。标准输入读完之后,得到一个k个String的RandomizedQueue,然后随机出队打印。这样可以满足extra challenge对于内存的要求。但是比较让人苦恼的是前面的入队概率一直想不出合适的,试过等值概率和一些渐变序列都失败了,造成的结果就是最后的k个值可能的组合不是均匀分布的,那么最后的输出的k个值的排列也一定不是均匀分布的,不满足题目要求。
后来在看Elementary sort部分的时候,老师介绍了一种随机打乱数组顺序的方法,而且据说已经被证明可以产生均匀分布的随机排列(代码如下)
public static void shuffle(Object[] a)
{
int N = a.length;
for (int i = 0; i < N; i++)
{
int r = StdRandom.uniform(i + 1);
exch(a, i, r); //交换数组中的 i 和 r 项
}
}
当时就想着这种思路能不能应用在那个extra challenge上,后来把算法稍微做了修改发现还真可以。
先简要叙述一下算法思路:
1首先标准输入前k项入队
2检查标准输入有无剩余项,若有转3,没有转4
3读取下一个输入(第n项),随机产生一个在1~n之间的随机数r,如果r <= k,则从RandomizedQueue随机出队一项,然后这次读取的String入队,否则转2
4结束
这个算法能够从n个String中随机产生均匀分布的k项组合,下面附上简单的证明过程(主要利用数学归纳法)

最后附上算法代码:
public static void main(String[] args){
int k = Integer.parseInt(args[0]);
RandomizedQueue<String> x = new RandomizedQueue<String>();
// use only one RandomizedQueue object of maximum size at most k
for (int i = 0; i < k; i++)
x.enqueue(StdIn.readString());
int n = k;
while (!StdIn.isEmpty()){
String string = StdIn.readString();
n++;
if (StdRandom.uniform(n) < k){
x.dequeue();
x.enqueue(string);
}
}
for (int i = 0; i < k; i++)
StdOut.println(x.dequeue());
}



