LeetCode 笔记系列13 Jump Game II [去掉不必要的计算]
题目: Given an array of non-negative integers, you are initially positioned at the first index of the array.
Each element in the array represents your maximum jump length at that position.
Your goal is to reach the last index in the minimum number of jumps.
For example:
Given array A = [2,3,1,1,4]
The minimum number of jumps to reach the last index is 2. (Jump 1 step from index 0 to 1, then 3 steps to the last index.)
当本娃拿到这个题目的时候,第一反应必然是dp。
解法一:

1 public static int jump(int[] A) { 2 // Start typing your Java solution below 3 // DO NOT write main() function 4 if(A.length < 2) return 0; 5 int[] dist = new int[A.length]; 6 int[] to = new int[A.length]; 7 for(int i = 0; i < A.length; i++){ 8 dist[i] = INFINITE; 9 } 10 dist[A.length - 1] = 0; 11 for(int i = A.length - 2; i >= 0; i--){ 12 int minDist = INFINITE; 13 for(int j = 1; j <= A[i] && i + j < A.length; j++){ 14 int nextIdx = i + j; 15 if(nextIdx < A.length){ 16 int candidate = dist[nextIdx] + 1; 17 if(candidate < minDist){ 18 minDist = candidate; 19 to[i] = nextIdx; 20 } 21 } 22 } 23 dist[i] = minDist; 24 } 25 return dist[0]; 26 }
然后,提交,大集合再次不过。。。WTF。。。
左思右想不得其解。
好在有leetcode讨论版,看到大牛的一个几行的代码。
NB闪闪的,就不折叠鸟。
解法二:
/* * We use "last" to keep track of the maximum distance that has been reached * by using the minimum steps "ret", whereas "curr" is the maximum distance * that can be reached by using "ret+1" steps. Thus, * curr = max(i+A[i]) where 0 <= i <= last. */ class Solution { public: int jump(int A[], int n) { int ret = 0; int last = 0; int curr = 0; for (int i = 0; i < n; ++i) { if (i > last) { last = curr; ++ret; } curr = max(curr, i+A[i]); } return ret; } };
O(n)的。。。。#我和我的小伙伴们都惊呆了#。
要理解这个算法,首先明白,这个题只要我们求跳数,怎么跳,最后距离是多少,都没让求的。
大牛这个算法的思想主要是,扫描数组(废话。。。),以确定当前最远能覆盖的节点,放入curr。然后继续扫描,直到当前的路程超过了上一次算出的覆盖范围,那么更新覆盖范围,同时更新条数,因为我们是经过了多一跳才能继续前进的。
形象地说,这个是在争取每跳最远的greedy。举个栗子。
比如就是我们题目中的[2,3,1,1,4]。初始状态是这样的:cur表示最远能覆盖到的地方,用红色表示。last表示已经覆盖的地方,用箭头表示。它们都指在第一个元素上。

接下来,第一元素告诉cur,最远咱可以走2步。于是:

下一循环中,i指向1(图中的元素3),发现,哦,i小于last能到的范围,于是更新last(相当于说,进入了新的势力范围),步数ret加1.同时要更新cur。因为最远距离发现了。

接下来,i继续前进,发现i在当前的势力范围内,无需更新last和步数ret。更新cur。

i继续前进,接下来发现超过当前势力范围,更新last和步数。cur已然最大了。
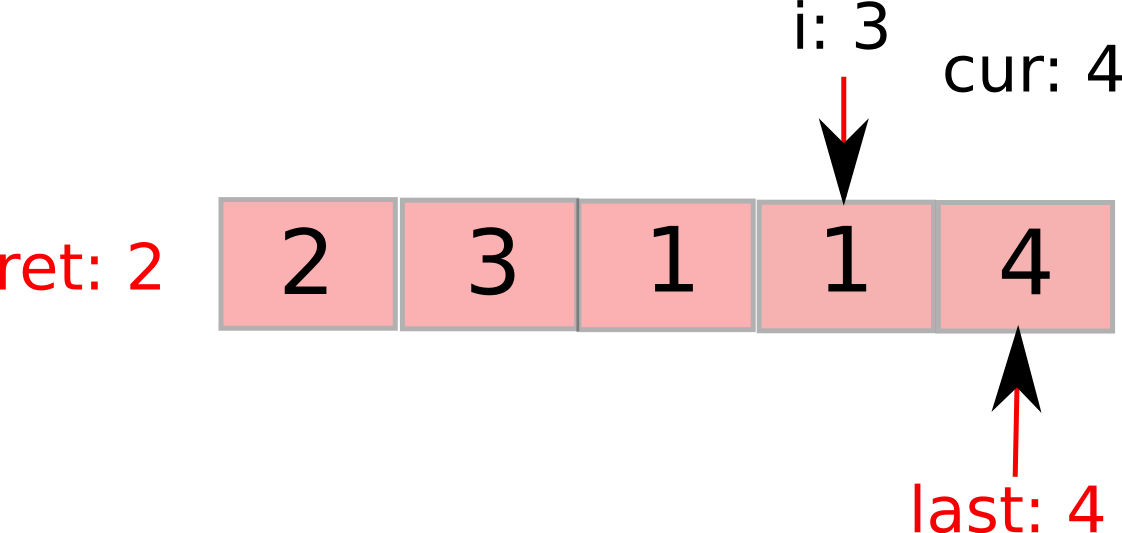
最后,i到最后一个元素。依然在势力范围内,遍历完成,返回ret。
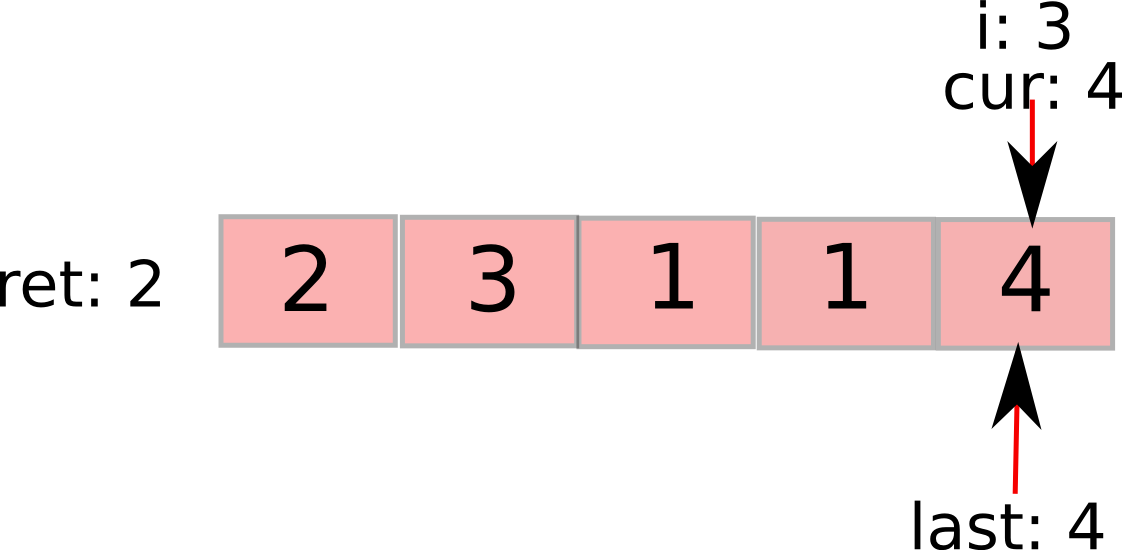
这道题让我们明白一个道理:
不要做无必要的计算。
对了,有同学会问,那为啥要用last,直接用curr跳不就行了。直接用curr跳那每次都是跳最远的,但是最优路径不不一定是这样。





【推荐】还在用 ECharts 开发大屏?试试这款永久免费的开源 BI 工具!
【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步