【可能产生的集合】

/*
无字典顺序集合 
说明： 
给定一组数字或符号 ， 产生所有可能的集合（包括空集合 ）， 例如给定1 2 3 ， 则可能的集合为 ：
{}、{1}、{1,2}、{1,2,3}、{1,3}、{2}、{2,3}、{3}。

解法： 
如果不考虑字典顺序，则有个简单的方法可以产生所有的集合，思考二进位数字加法，并注意
1出现的位置，如果每个位置都对应一个数字，则由1所对应的数字所产生的就是一个集合，例
如：
000     {}
001     {3}
010     {2}
011     {2,3}
100     {1}
101     {1,3}
110     {1,2}
111     {1,2,3}

了解这个方法之后，剩下的就是如何产生二进位数？有许多方法可以使用，您可以使用unsigne型别加上&位元运算来产生，这边则是
使用阵列搜 寻，首先阵列内容全为0，找第一个1，在还没找到之前将走访过的内容变为0，而第一个找到的0则变为 1，如此重复直
到所有的阵列元素都变为1为止，例如：
000 => 100 => 010 => 110 => 001 => 101 => 011 => 111
如果要产生字典顺序，例如若有4个元素，则：
{} => {1} => {1,2} => {1,2,3} => {1,2,3,4} =>
{1,2,4} =>
{1,3} => {1,3,4}  =>
{1,4} =>
{2} => {2,3} => {2,3,4} =>
{2,4} =>
{3} => {3,4} =>
{4}

简单的说，如果有n个元素要产生可能的集合，当依序产生集合时，如果最后一个元素是n，而倒数第二个元素是m的话，例如：
{a b c d e n}

则下一个集合就是{a b c d e+1}，再依序加入后续的元素。

例如有四个元素，而当产生{1 2 3 4}集合时，则下一个集合就是{1 2 3+1}，也就是{1 2 4} ，由 于最后一个元素还是4，所以下一
个集合就是{1 2+1}，也就是{1 3}，接下来再加入后续元素4，也就是{1 3 4}，由于又遇到元素4，所以下一个集合是{1 3+1}，也就是{1 4}。
*/


#include<stdio.h>
#include<stdlib.h>

#define MAXSIZE 20

int main(void)
{
    char digit[MAXSIZE];
    int i, j;
    int n;
    
    printf("输入集合个数：");
    scanf("%d", &n);
    
    for(i = 0; i < n; i++)
    {
        digit[i] = '0';
    }
    
    printf("\n{}");
    
    while(1)
    {
        for(i = 0; i < n && digit[i] == '1'; digit[i] = '0', i++);
        
        if(i == n)
        {
            break;
        }
        else
        {
            digit[i] = '1';
        }
        for(i = 0; i < n && digit[i] == '0'; i++);
        printf("\n{%d", i + 1);
        
        for(j = i + 1; j < n; j++)
        {
            if(digit[j] == '1')
            {
                printf("%d", j + 1);
            }
        }
        printf("}");
    }
    printf("\n");    
    return 0;
}

 运行结果：

 

 

/*
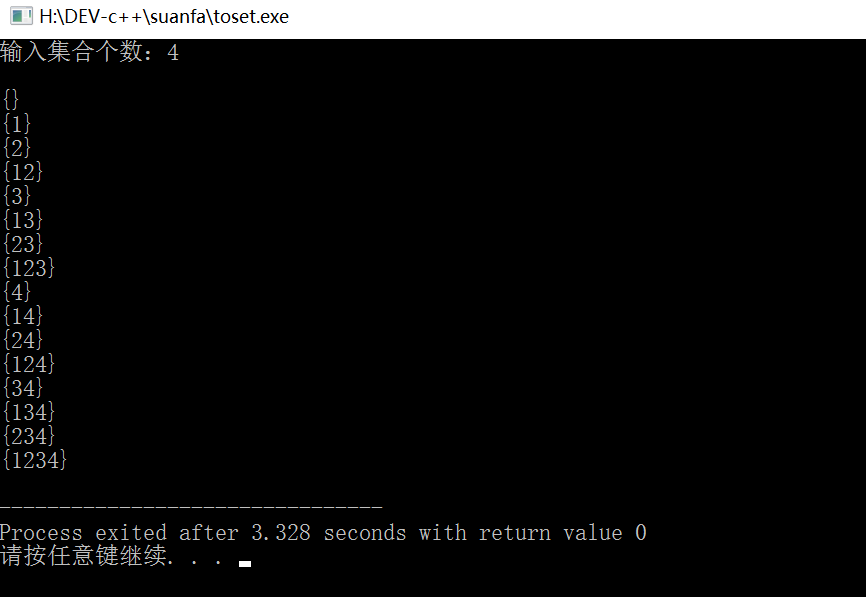
有字典顺序集合 
*/

#include<stdio.h>
#include<stdlib.h>

#define MAXSIZE 20

int main(void)
{
    int set[MAXSIZE];
    int i, n, position = 0;
    
    printf("输入集合个数：");
    scanf("%d", &n);
    printf("\n{}");
    set[position] = 1;
    
    while(1)
    {
        printf("\n{%d", set[0]);
        for(i = 1; i <= position; i++)
        {
            printf("%d", set[i]);
        }
        printf("}");
        if(set[position] < n)
        {
            set[position + 1] = set[position] + 1;
            position++;
        }
        else if(position != 0)
        {
            position--;
            set[position]++;
        }
        else
        {
            break;
        }
    }
    printf("\n");
    
    return 0;
}

 

运行结果：