【格雷码】
/* 格雷码 说明: Gray Code是一个数列集合 ,每个数使用二进位来表示 ,假设使用n位元来表示每个数好了 ,任两个数之间只有一个位元值不同, 例如以下为3位元的Gray Code: 000 001 011 010 110 111 101 100 由定义可以知道,Gray Code的顺序并不是唯一的,例如将上面的数列反过来写,也是一组GrayCode: 100 101 111 110 010 011 001 000 Gray Code是由贝尔实验室的Frank Gray在1940年代提出的,用来在使用PCM(Pusle CodeModulation)方法传送讯号时避免出错, 并于1953年三月十七日取得美国专利。 解法: 由于Gray Code相邻两数之间只改变一个位元,所以可观 察Gray Code从1变0或从0变1时的位置,假设有4位元的Gray Code如下: 0000 0001 0011 0010 0110 0111 0101 1000 1100 1101 1111 1110 1010 1011 1001 1000 观察奇数项的变化时,我们发现无论它是第几个Gray Code,永远只改变最右边的位元,如果是1就改为0,如果是0就改为1。 观察偶数项的变化时,我们发现所改变的位元,是由右边算来第一个1的左边位元。 以上两个变化规则是固定的,无论位元数为何;所以只要判断位元的位置是奇数还是偶数,就可以决定要改变哪一个位元的值,为了 程式撰写方便,将阵列索引 0当作最右边的值,而在列印结果时,是由索引数字大的开始反向列印。 将2位元的Gray Code当作平面座标来看,可以构成一个四边形,您可以发现从任一顶点出发,绕四边形周长绕一圈,所经过的顶点座 标就是一组Gray Code,所以您可以得到四组GrayCode。 同样的将3位元的Gray Code当作平面座标来看的话,可以构成一个正立方体,如果您可以从任一顶点出发,将所有的边长走过,并不 重复经过顶点的话,所经过的顶点座标顺序之组合也就是一组Gray Code。 */ #include<stdio.h> #include<stdlib.h> #define MAXBIT 20 #define TRUE 1 #define CHANGE_BIT(x) x = ((x) == '0' ? '1':'0') #define NEXT(x) x = (1 - (x)) int main(void) { char digit[MAXBIT]; int i, bits, odd; printf("输入位元数:"); scanf("%d", &bits); for(i = 0; i < bits; i++) { digit[i] = '0'; printf("0"); } printf("\n"); odd = TRUE; while(1) { if(odd) { CHANGE_BIT(digit[0]); } else { for(i = 0; i < bits && digit[i] == '0'; i++); if(i == bits - 1) { break; } CHANGE_BIT(digit[i+1]); } for(i = bits - 1; i >= 0; i--) { printf("%c", digit[i]); } printf("\n"); NEXT(odd); } return 0; }
运行结果:
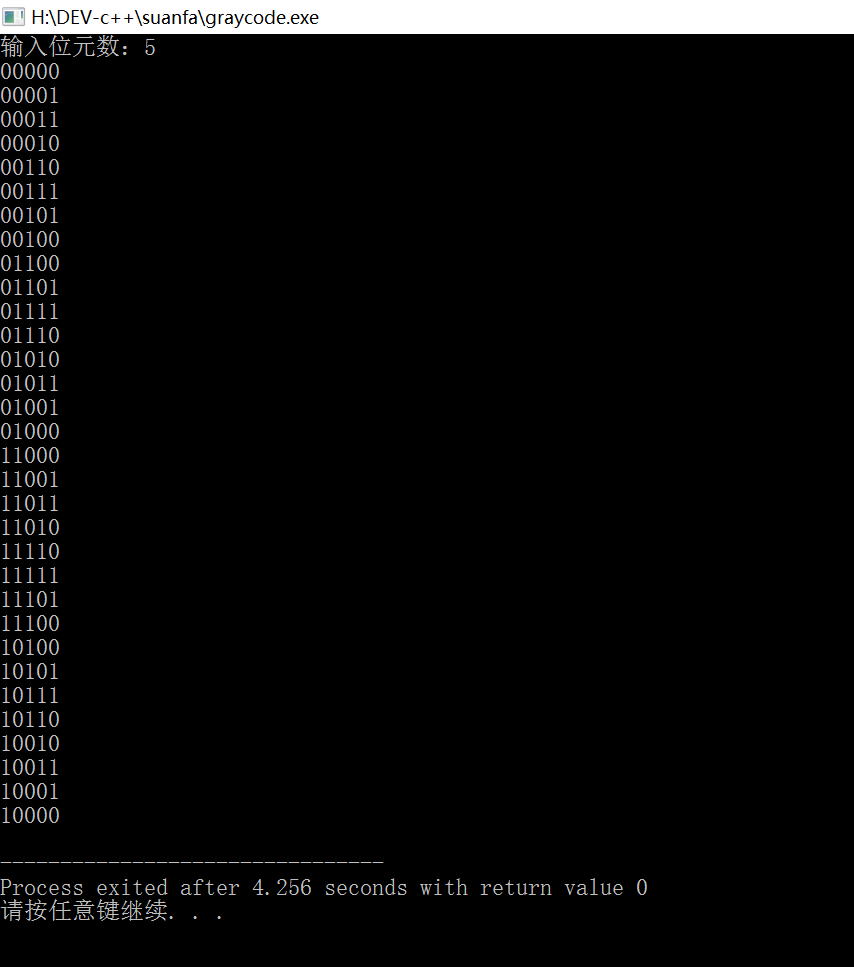
转载本博请联系作者! 如有问题请在评论区评论或者发邮件:@libras


