【完美数 】

/*
完美数 

说明：
如果有一数n ，其真因数 （Proper factor ） 的总和等于n ， 则称之为完美数（Perfect Number ），例如以下几个数都是完美数：
6 = 1 + 2 + 3
28 = 1 + 2 + 4 + 7 +  14
496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248
程式基本上不难，第一眼看到时会想到使用回圈求出所有真因数，再进一步求因数和，不过若n值很大，则此法会花费许多时间在回圈测试上，十分
没有效率，例如求小于10000的所有完美数 。

解法：
如何求小于10000的所有完美数？并将程式写的有效率？基本上有三个步骤：
1.求出一定数目的质数表
2.利用质数表求指定数的因式分解
3.利用因式分解求所有真因数和，并检查是否为完美数

步骤一 与 步骤二 在之前讨论过了，问题在步骤三，如何求真因数和？方法很简单，要先知道将所有真因数和加上该数本身，会等于该数的两倍，
例如：
2 * 28 = 1 + 2 + 4 + 7 + 14 + 28
等式后面可以化为：
2 * 28 = (2^0 + 2^1 + 2^2) * (7^0 + 7^1 )
所以只要求出因式分解，就可以利用回圈求得等式后面的值，将该值除以2就是真因数和了；等式后面第一眼看时可能想到使用等比级数公式来解,不
过会使用到次方运算，可以在回圈走访因式分解阵列时，同时计算出等式后面的值，这在下面的实作中可以看到


*/

#include <stdio.h>
#include <stdlib.h>

#define N 1000
#define P 10000

int prime(int*); // 求质数表
int factor(int*, int, int*); // 求factor
int fsum(int*, int); // sum ot proper factor

int main(void) {
    int ptable[N+1] = {0}; // 储存质数表
    int fact[N+1] = {0}; // 储存因式分解结果
    int count1, count2, i;
    
    count1 = prime(ptable);
    
    for(i = 0; i <= P; i++) {
        count2 = factor(ptable, i, fact);
        if(i == fsum(fact, count2))
            printf("Perfect Number: %d\n", i);
    }
    printf("\n");
    return 0;
}

int prime(int* pNum) {
    int i, j;
    int prime[N+1];
    for(i = 2; i <= N; i++)
        prime[i] = 1;
    for(i = 2; i*i <= N; i++) {
        if(prime[i] == 1) {
            for(j = 2*i; j <= N; j++) {
                if(j % i == 0)
                    prime[j] = 0;
            }
        }
    }
    for(i = 2, j = 0; i < N; i++) {
        if(prime[i] == 1)
            pNum[j++] = i;
    }
    return j;
}

int factor(int* table, int num, int* frecord) {
    int i, k;
    for(i = 0, k = 0; table[i] * table[i] <= num;) {
        if(num % table[i] == 0) {
            frecord[k] = table[i];
            k++;
            num /= table[i];
        }
        else
            i++;
    }
    frecord[k] = num;
    return k+1;
}

int fsum(int* farr, int c) {
    int i, r, s, q;
    i = 0;
    r = 1;
    s = 1;
    q = 1;
    while(i < c) {
        do {
            r *= farr[i];
            q += r;
            i++;
        } while(i < c-1 && farr[i-1] == farr[i]);
        s *= q;
        r = 1;
        q = 1;
    }
    return s / 2;
}

 

结果：

 ====================================================

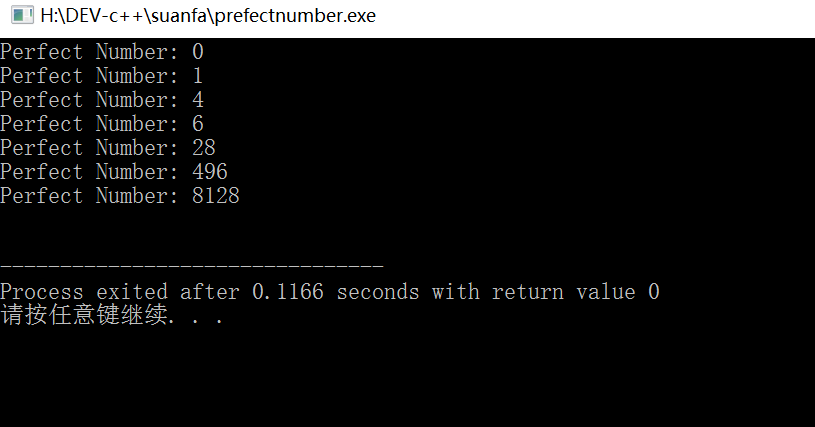
谢谢@小时候嘚小时候提醒，4，1，0确实不是完美数，程序应该存在bug，