【骑士走棋盘】

/*
骑士走棋盘
说明：
骑士旅游Knight tour在十八世纪初倍受数学家与拼图迷的注意，它什么时候被提出已不可考，骑士的走法为西洋
棋的走法，骑士可以由任一个位置出发，它要如何走完所有的位置。

解法:
骑士的走法,基本上可以用递回来解决,但是纯粹的递回在维度大时相当没有效率,一个聪明的解法由J.CWarnsdorff
在1823年提出， 简单地说，先将最难的位置走完，接下来的路就宽广了，骑士所想要的下一步，为下一不再 选
择时，所能走的步数最少的一步。使用这个方法，在不使用递回的情况下，可以有较高的机率找出走法（找不到走
的机率也是有的） 
*/ 
#include <stdio.h>

int pos[8][8] = {0};

int travel(int, int);

int main()
{
    int i, j, startX, startY;
    while(1)
    {
        printf("输入起始点：");
        scanf("%d%d", &startX, &startY);
        if(travel(startX, startY)) {
            printf("游历完成！\n");
        }else {
            printf("游历失败！\n");
        }
        for(i=0; i<8; i++) {
            for(j=0; j<8; j++) {
                printf("%2d ", pos[i][j]);
            }
            printf("\n");
        }
        printf("\n");
    }
    
    return 0;
}

int travel(int x, int y) {
    int i, j, k, l, m;
    int tmpX, tmpY;
    int count, min, tmp;

    //骑士可走的八个方向(顺时针)
    int ktmoveX[8] = {1, 2, 2, 1, -1, -2, -2, -1};
    int ktmoveY[8] = {-2, -1, 1, 2, 2, 1, -1, -2};

    //测试下一步坐标
    int nextX[8] = {0};
    int nextY[8] = {0};

    //记录每个方向的出路的个数
    int exists[8] = {0};

    //起始用1标记位置
    i = x;
    j = y;
    pos[i][j] = 1;

    //遍历棋盘
    for(m=2; m<=64; m++) {
        //初始化八个方向出口个数
        for(l=0; l<8; l++) {
            exists[l] = 0;
        }
        l = 0; //计算可走方向

        //试探八个方向
        for(k=0; k<8; k++) {
            tmpX = i + ktmoveX[k];
            tmpY = j + ktmoveY[k];
            //边界 跳过
            if(tmpX<0 || tmpY<0 || tmpX>7 || tmpY>7) {
                continue;
            }
            //可走 记录
            if(pos[tmpX][tmpY] == 0) {
                nextX[l] = tmpX;
                nextY[l] = tmpY;
                l++;    //可走方向加1
            }
        }
        count = l;
        //无路可走 返回
        if(count == 0) {
            return 0;
        //一个方向可走 标记
        }else if(count == 1) {
            min = 0;
        //找出下个位置出路个数
        }else {
            for(l=0; l<count; l++) {
                for(k=0; k<8; k++) {
                    tmpX = nextX[l] + ktmoveX[k];
                    tmpY = nextY[l] + ktmoveY[k];
                    if(tmpX<0 || tmpY<0 || tmpX>7 || tmpY>7) {
                        continue;
                    }
                    if(pos[tmpX][tmpY] == 0) {
                        exists[l]++;
                    }
                }
            }
            //找出下个位置出路最少的方向
            min = 0;
            tmp = exists[0];
            for(l=0; l<count; l++) {
                if(exists[l] < tmp) {
                    tmp = exists[l];
                    min = l;
                }
            }
        }
        //用序号标记走过的位置
        i = nextX[min];
        j = nextY[min];
        pos[i][j] = m;
    }
    return 1;
}

 

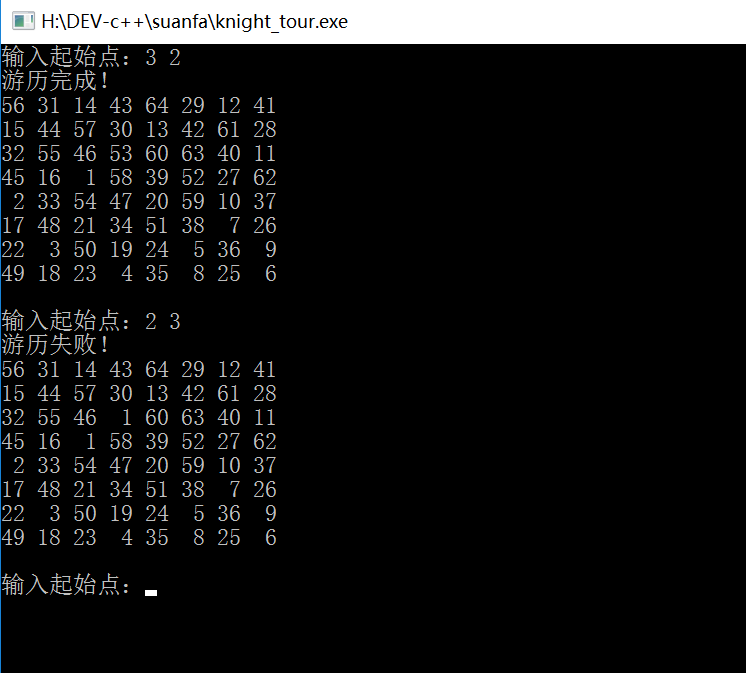
运行结果：