ng-深度学习-课程笔记-5: 深层神经网络(Week4)

1 深度L层神经网络( Deep L-layer Neural network )

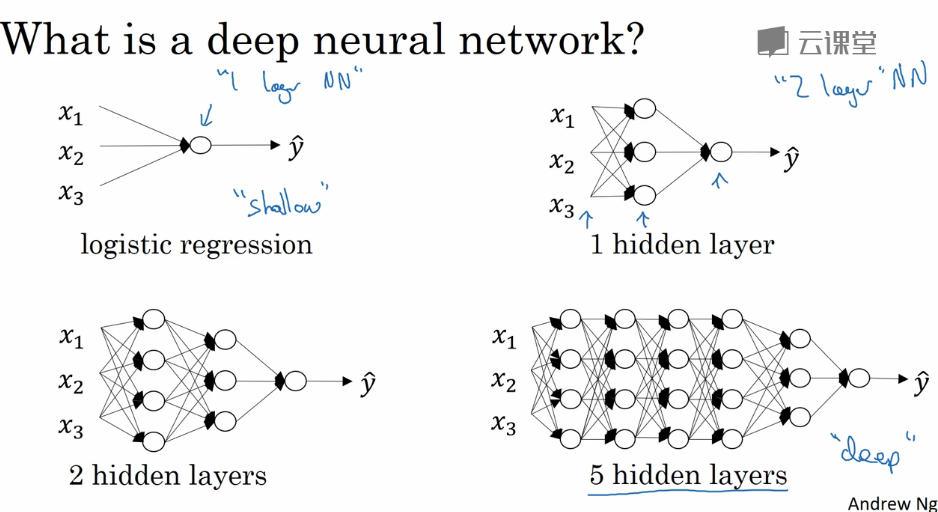
针对具体问题很难判断需要几层的网络，所以先试试逻辑回归是比较合理的做法，然后再试试单隐层，把隐层数量当作一个超参数，在验证集上进行评估。

对于深层神经网络，只是在单隐层的基础上拓展多几层，符号约定也类似。（深层没有官方的定义，一般三层或三层以上就可以认为是深层，这是相对单隐层的两层而言的，深浅是成程度上的相对）

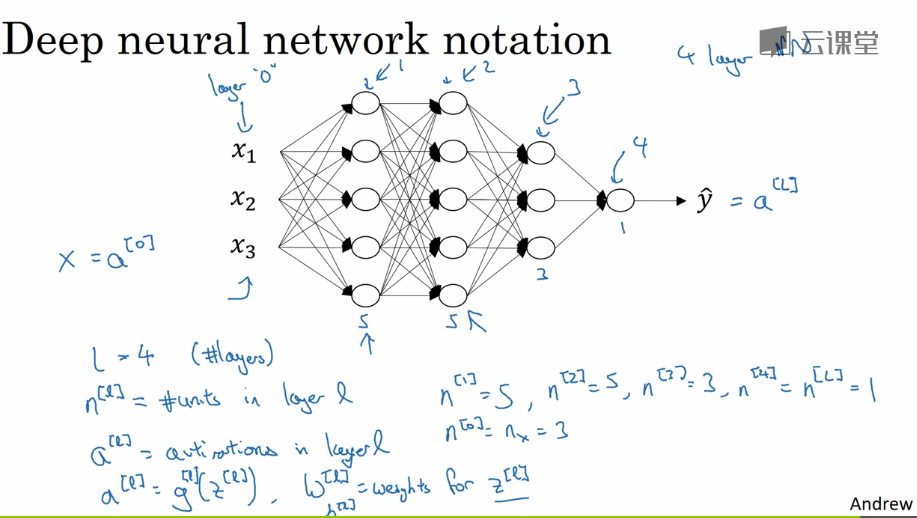
这里重新声明下，L表示层数，$n^{[0]}$代表输入层单元数（也写作$n_x$代表特征数），$n^{[1]}$代表第1个隐层的单元数，$n^{[2]}$代表第2个隐层的单元数，...，$n^{[L]}$代表输出层的单元数。

权重w，权重和z类似，上标l表示从l-1层到l层的权重，权重和。激活输出，上标l表示l层的输出。

 

 

2 前向传播( Forward Propagation in a Deep Network )

根据浅层网络的输出计算可以类推出深层网络的前向传播，公式其实都差不多，只不过是重复多几次，这里不再阐述。

计算时要用到for循环，没办法完全向量化，因为我们需要计算一层的激活，再用这个激活去计算下一层，这种情况只能用for循环。

 

3 核对矩阵维度( Getting your matrix dimensions right )

实现神经网络的时候，想减少出bug的概率，需要系统化地去思考矩阵的维度，ng表示在debug的时候会用笔纸很小心地过一遍矩阵维度的检查。

X维度为( $n^{[0]}$，m）；

ｗ上标l的维度为（$n^{[l]}$，$n^{[l-1]}$）；　b上标l的维度为（$n^{[l]}$，m）；

$dw^{[l]}$的维度和$w^{[l]}$一样，$db^{[l]}$的维度和$b^{[l]}$的维度一样；

A上标l的维度，Z上标i的维度，b上标i的维度一样。

 

4 为什么使用深层表示( Why deep representations )

一个解释就是图像识别中，用多层，前几层提取一些简单的特征，后几层组合特征，到比如第一层提取边缘，第二层提取眼鼻嘴耳，第三层得到的是眼鼻嘴耳组成的人脸。

再比如语音识别中，前几层用来学习每个音节的发音，后几层组成一个单词。

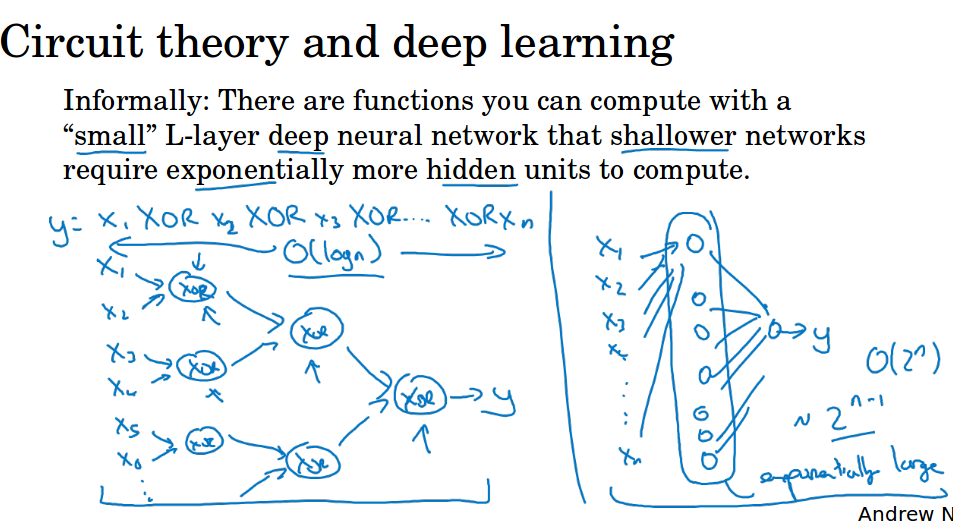
第二个解释就是，有很多数学函数用深网络比浅网络要容易学习得多，比如很多个数异或，用深网络，学习到一棵树，计算复杂度为logN。用单隐层学习的话，需要$2^{n-1}$个隐藏单元。

稍微解释一下这个$2^{n-1}$，两个数异或的逻辑表达式y = A‘B + AB'，需要两个乘式，也就是2的(2-1)次方个。

三个数异或的时候y = (A’B + AB') ' C +   (A’B + AB') C'，展开会有四个乘式，也就是2的(3-1)次方个。

容易推到，n个数异或的时候，需要$2^{n-1}$个乘式相加，所以我们需要$2^{n-1}$个隐藏单元。

从逻辑表达式就可以理解，因为每异或多一个数，我们的乘式会加倍。

 

5 前向和反向传播( Forward and backward propagation )

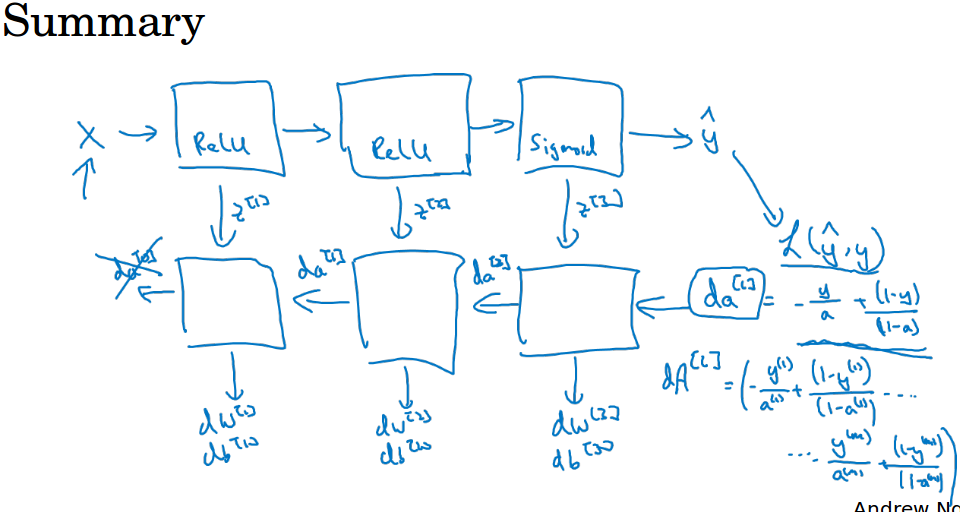
前向计算，对于每一层，输入$a^{[l-1]}$，输出$a^{[l]}$，其中输入层的$a^{[0]}$为原始特征。为了便于后面的求导，把中间的z也缓存起来。

反向传播，对于每一层，输入$da^{[l]}$，输出$da^{[l-1]}$，$dw^{[l]}$，$db^{[l]}$，为了求出这些，需要计算中间导数$dz^{[l]}$。

这些公式看起来有些繁琐复杂，ng的建议是自己动手做一下，做一下能让你更具体地掌握它，虽然在实现一个算法的时候，ng有时候也会惊讶，怎么莫名其妙就成功了。

那是机器学习里面的复杂性是来源于数据本身，而不是一行行的代码。所以有时候你实现了几行代表但是不太确定它具体做了什么，却神奇般的实现了。

 

 

 

6 参数和超参数( Ｐarameter and Hyperparameters )

随着梯度下降而更新的w和b称为参数。

学习率，迭代次数，隐层个数，每个隐层的单元数，激活函数的选择，batch大小，正则化参数，动量等等这些称为超参数，它们是事先选择确定的。

超参数对参数w和b有所影响，可以理解为参数的参数。实际中很难确切知道超参数的最优值是多少。

今天的深度学习还是很经验性的过程，超参数的选择有很多可能，你要尝试各种不同的选择。可以迭代多个值，画个图，寻找合适的值。

深度学习用于解决很多问题，计算机视觉，语音识别，自然语言处理，很多结构化的数据应用比如网络广告，网页搜索，产品推荐等等。

ng所看过的就有很多领域的研究员，这些领域的一个，尝试不同的设置，有时候这种超参数的直觉，可以推广，但有时又不会。

所以ng经常建议人们，特别是刚开始应用新问题的人，去试一定范围的值看看结果如何。

其实，就算已经用了很久的模型，比如网络广告，可能在你开发途中，很有可能学习率的最优数值或者其它超参数的最优值，是会变的。

所以即使你每天都在用当前最优的参数调试你的系统，还是会发现突然最优值怎么没用了，可能cpu，gpu，网络，数据什么东西改变了。

（我觉得有时可能是数据变了，像网络广告这种东西，随着人们的口味变化，你的模型需要做调整）

所以有一条经验规律：可能你的模型过几个月就需要调整，只要经常尝试不同的超参数，勤于检验结果，看看有没有更好的超参，相信你会慢慢得到设定超参的直觉，知道你的问题最好用什么样的参数。

深度学习比较让人不满的一部分也就是你必须尝试很多次不同可能性，但参数设定这个领域，深度学习研究还在进步中，相信过段时间会有比较好的方法出现。

 

7 这和大脑有什么关系( What does this have to do with the brain )

我们通常把人工神经元类比生物神经元，说它模拟大脑的行为，其实是过度简化了。

但这种形式（人工神经元）更为简洁，也让普通人更愿意公开讨论，也方便新闻媒体报道，并且吸引大众眼球。

但是这个类比还是很粗略的，用神经网络中的一个逻辑单元类比大脑中的生物神经元，输入的特征类比输入的电信号，当权重和被激活后，电信号沿着轴突传到另一个神经元。

至今为止其实连神经科学家们都很难解释究竟一个神经元能做什么，一个小小的神经元其实是极其复杂的。

它的一些功能，可能真的是类似逻辑回归的运算，但单个神经元究竟在做什么，目前没有人能够真正解释，大脑中的神经元是如何学习的，至今这仍是一个迷之过程。

虽然深度学习确实是个很好的工具，能学习到各种很灵活很复杂的函数，但这种和生物神经元的对比，在这个领域的早期也许值得一提，但现在这种类比已经逐渐过时了，ng自己也在尽量少用这种说法。