ng-深度学习-课程笔记-2: 神经网络中的逻辑回归(Week2)

1 二分类( Binary Classification )

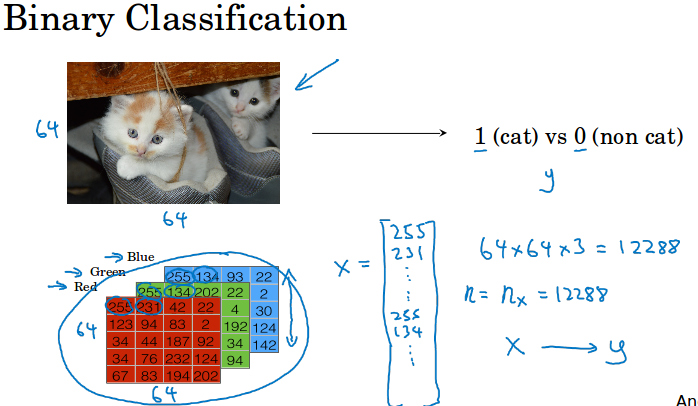
逻辑回归是一个二分类算法。下面是一个二分类的例子，输入一张图片，判断是不是猫。

输入x是64*64*3的像素矩阵，n或者nx代表特征x的数量，y代表标签0/1，m代表训练集的样本总数。

本门课中：X代表所有的输入x，x按列排列，每个x是一个列向量，Ｘ的shape是( n, m )。

同理Y也按列排序，shape为( 1, m )。

 

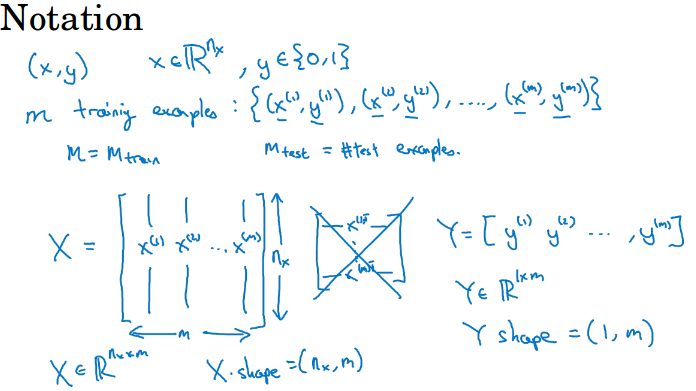
2 逻辑回归( Logistic Regression )

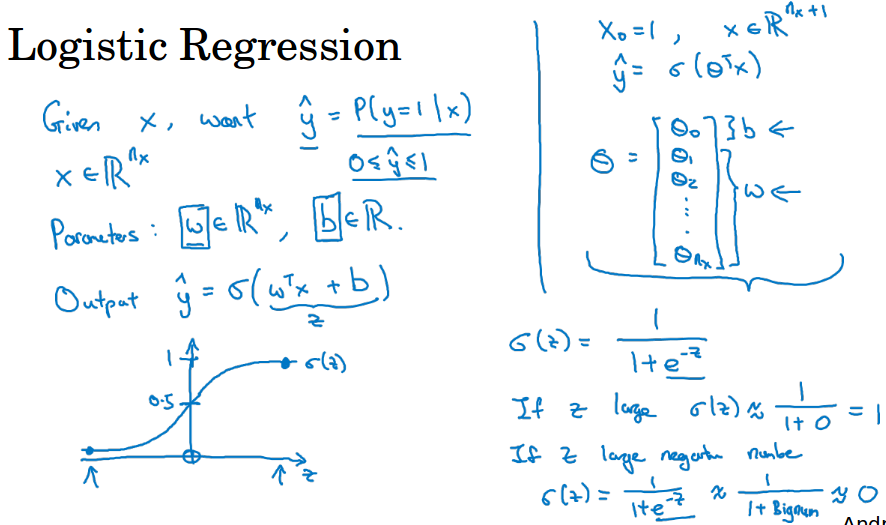
给定一个输入x ( 比如图像)，你想得到一个$ \;\hat{y}\; $ ，这个$ \;\hat{y}\; $为给定x的情况下y为1的概率，正如上一节的例子中图像为猫的概率。

参数w和x的维度相同，参数b是一个实数，所以给出输入和这些参数，如果你做$ w^{T}+b $，这往往用在线性回归模型。

这里你想要输出一个概率，所以我们加上一个sigmoid函数，它可以把所有实数压缩在0到1之间。

这里让$ z =  w^{T}+b $，有$ \;\hat{y}\; = \sigma (z) $，z无穷大的时候概率约等于1，z无穷小的时候概率约等于0。

所以我们要实现的就是找一组参数w和b使得$ \;\hat{y}\; $能够做出好的预测（预测y等于1的概率）。

有另一种写法，如下图右上角所示，把b变成w0，然后x0为1，这样w和x就多了一维，这里用θ来表示n+1维的w。注意一下本门课不这么用。

 

3 代价函数( Cost Function )

ps: 约定用上标表示训练集数据的编号，用下标表示特征编号。

代价函数表示模型预测结果和真实结果的差距度量，代价函数是所有样本的损失函数加起来。

损失函数( loss function)代表的是单个样本的损失，loss函数用L( loss )表示，通常均方损失( mean square error )用于线性回归。

在逻辑回归中我们不用均方损失，如果使用均方损失，损失函数是非凸的，在之后的梯度下降时会得到多个局部最小( local minimum )。

为了使loss为凸函数（利于优化），我们使用如图所示loss（下面那个L，带log的）。然后讲讲这个loss的合理性（这里没有按图中的解释）。

y等于1时候，对于该loss函数，当$ \;\hat{y}\; $越接近1时，loss越接近0，损失越小。

y等于0的时候，对于该loss函数，$ \;\hat{y}\; $越接近0时，loss越接近0，损失越小。

我们就是要让loss越小越好，所以对loss做梯度下降找最小值，恰恰对应了我们让$ \hat{y} $接近y的这个过程。

上面给的L是单个训练样本的损失函数，最后一行我们给出了整个训练集的代价函数J，就是把这些所有数据的损失累加起来。

所以我们要做的就是找到W和B，使得损失函数J最小。这里用大写W和B是因为考虑所有的数据，正如X和Y对应x和y一样。

 

4 梯度下降( gradient descent )

我们用梯度下降来找到w和b，使得代价函数J最小。下图给出了J(w, b)的曲线图，是一个凸函数。实际上w可以是高维向量，为了画图理解，这里w和b都用的实数。

当我们初始化w和b时，可能处在曲线上的某一个点，梯度下降要做的就是逐渐往谷底方向走一小步接近最小值，一般会迭代一定次数或者cost小于某个值的时候停止。

 

看看具体的计算公式，我们先只看w，不考虑b。

J(w)曲线如图所示，梯度下降就是一直重复$w = w - \alpha * J^{\;'} (w)$的过程。

α为学习率，控制着下降的步伐有多大，$J^{\;'} (w)$是导数( derivative )。

如图中的例子，假如从右边的初始点出发，$J^{\;'} (w)$为正，导数在这里也就是切线的斜率，我们让$w = w - \alpha * J^{\;'} (w)$就是让w向左减小，就是让初始点朝着最小点靠近。

假设从左边的初始点出发，$J^{\;'} (w)$为负，我们让$w = w - \alpha * J^{\;'} (w)$就是让w向右增加，也是让初始点朝着最小点靠近。

当把b考虑进来，J是含有两个变量的函数，原来的导数就变成了偏导数( partial derivative )，求导符号有所变化。

 

5 计算图的导数计算( derivatives with a computation graph )

当一个函数含有多个变量且内嵌了很多个函数时，求导比较麻烦，变量又多，又要用好多次链式法则，比如在利用bp算法训练神经网络的时候。

可以使用计算图来理解求导的过程，先列出前向计算公式，然后根据公式反向求导，这样去看思路就会比较清晰。

 

 

6 逻辑回归中的梯度下降( Logistic Regression Gradient Descent )

为了便于理解，ng使用计算图来讲解逻辑回归中的梯度下降（虽然在逻辑回归中没什么必要用计算图）。

这里假设有两个特征，第一张图用计算图展示了单个样本的求导过程，第二张图把所有样本的加起来做求导和梯度下降。

这里给出的算法用了两个for循环，实际上我们会利用向量化代替for循环来加速运算，向量化的内容见下一节课。

 

 

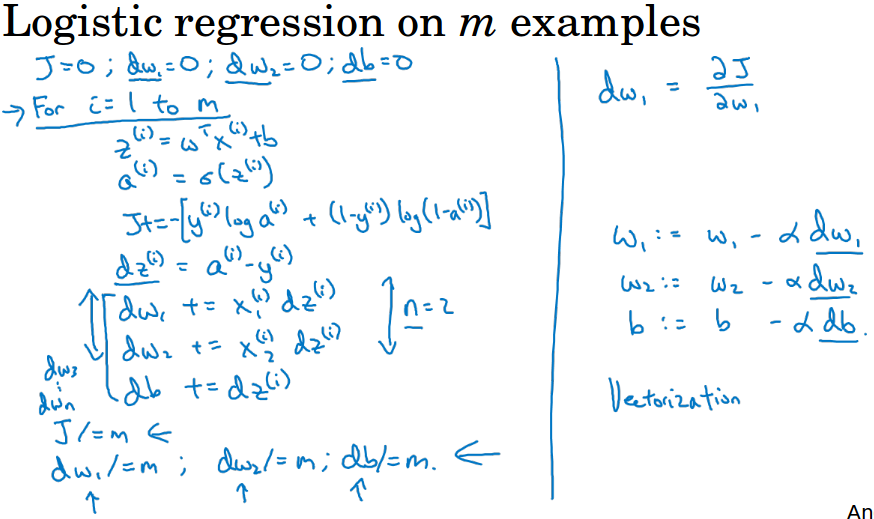
7 logistic代价函数的解释( Explanation of logistic regression cost function)

线性回归中的平方损失是很天然的想法就想到用这种损失来度量预测和真实之间的差距。

逻辑回归中的代价函数给人感觉很突然，怎么突然就有这么个东西。

虽然它符合了我们优化的思想（在最小化这个代价函数的过程对应了我们让预测值逼近真实值的过程），但是还是不知道它是怎么产生的。

这里ng给出了简洁的证明，解释了我们的代价函数为什么是这种形式。

 

7.1 单个样本的损失函数解释

$ \hat{y} $是给定x时y等于1的概率，$ \hat{y}  = P(\;y = 1\;|\;x\;) $，这是我们给出的预测概率。

那么当y的真实值为1时，在给定x下预测y正确的概率为$ \hat{y} $。

当y的真实值为0时，在给定x下预测y正确的概率为1 - $ \hat{y} $，也就是预测为0的概率。

$ If \quad y=1, \quad P(\;y\;|\;x\;) = \hat{y} $

$ If \quad y=0, \quad P(\;y\;|\;x\;) = 1 - \hat{y} $

合并后得到 $ P(\;y\;|\;x\;) = \hat{y}\;^{y}\;*(1-\hat{y})^{(1-y)} $

我们要使给定x下预测y正确的概率P ( y | x ) 最大，也就是使log P( y | x )最大，展开后得到的是：

$ log\;[\;\hat{y}\;^{y}\;*(1-\hat{y})^{(1-y)}\;]=y\;log\;\hat{y}\; + (1-y)\;log\;(1-\hat{y}) $

这个东西就是负的损失函数 $ - L( \hat{y}, y) $，损失函数之前讲过。

所以我们最大化这个$ log P(\;y\;|\;x\;) $，就是最小化损失函数，这样就和前面讲的损失函数串起来了。

事实上这个损失函数叫做交叉熵cross-entropy，是从信息论中引进来的。

关于交叉熵的相关知识我总结在另一篇博文：http://www.cnblogs.com/liaohuiqiang/p/7673681.html

 

以下是推导过程：

预测$ \quad\hat{y} = \sigma(w^{T}+b), \quad where \quad \sigma(z)= \frac{1}{1+e^{-z}} $

有　$ \hat{y} = P(\;y\;=1\;|\;x\;) $

可以推出：

　　$ \left.\begin{matrix}If \quad y=1, \quad P(\;y\;|\;x\;) = \hat{y} &  & \\If \quad y=0, \quad P(\;y\;|\;x\;) = 1 - \hat{y}&  & \end{matrix}\right\} \Rightarrow P(\;y\;|\;x\;) = \hat{y}\;^{y}\;*(1-\hat{y})^{(1-y)} $

最大化预测概率：

　　$max\left\{\;P(y|x)\;\right\} \Leftrightarrow max\left\{\;log\;P(y|x)\;\right\}$　

　　$log\;P(\;y\;|\;x\;) = log\;[\;\hat{y}\;^{y}\;*(1-\hat{y})^{(1-y)}\;]$

　　$=y\;log\;\hat{y}\; + (1-y)\;log\;(1-\hat{y})$

　　$=- L( \hat{y}, y) $

显然有：$max\left\{\;log\;P(\;y\;|\;x\;)\;\right\}\Leftrightarrow min\left\{\;L( \hat{y}, y) \;\right\} $

 

7.2 m个样本的代价函数解释

先假设训练样本中所有的样本服从同一分布且相互独立，那么整个训练集预测正确的概率P等于每个样本预测正确的概率的乘积。

有$ P = \prod _{i=1}^{m} P ( \;y^i\; | \;x^i\; ) $，根据极大似然估计法，你想要训练的模型能使得预测该分布下的所有数据的准确率最大，就是要使所有观测样本（也就是训练样本）预测正确的概率的乘积最大。

所以我们就是要最大化这个P，也就是最大化$ log P $，因为log是单调递增的。

$ log\;P = \sum_{i=1}^{m} log\;P ( \;y^i\; | \;x^i\; ) $。

而我们在上一小节已经得到$ log\;P ( \;y^i\; | \;x^i\; ) = - L( \hat{y}, y) $，所以我们只要累加这个负的损失函数，使这个和最大。

累加（负的损失函数）得到的和，也就是（累加损失函数的和）的负，也就对应了代价函数的负值，因为代价函数就是多个样本的损失函数的和，还需要除以m求平均。

要让代价函数的负值最大，也就是让代价函数J( w, b) 最小，这正对应了我们前面的优化目的。