图

1.学习总结(2分)

1.1图的思维导图

1.2 图结构学习体会

一、深度遍历算法

　　1.定义：首先访问出发点v，并将其标记为已访问过；然后依次从v出发搜索v的每个邻接点w。若w未曾访问过，则以w为新的出发点继续进行深度优先遍历，直至图中所有和源点v有路径相通的顶点(亦称为从源点可达的顶点)均已被访问为止。若此时图中仍有未访问的顶点，则另选一个尚未访问的顶点作为新的源点重复上述过程，直至图中所有顶点均已被访问为止。

　　2.体会：无论是以邻接表还是以邻接矩阵作为存储结构，核心思想是利用递归算法重复操作。通过一个赋初值为0的visited[]数组，在递归过程中若节点对应的visited数为0则说明未访问，继续递归并赋值一个非0数，反之继续访问下一个节点。

　　二、广度遍历算法

　　1.定义：（1）、从图中某个顶点V0出发，并访问此顶点；

　　　　　　（2）、从V0出发，访问V0的各个未曾访问的邻接点W1，W2，…,Wk;然后,依次从W1,W2,…,Wk出发访问各自未被访问的邻接点；

　　　　　　（3）、重复步骤2，直到全部顶点都被访问为止

　　2.体会：广度优先遍历是将一个节点的所有邻接点都访问后在访问下一个节点，比起深度优先遍历的递归算法相对更好理解，尤其是在以邻接表为存储结构的情况下，代码容易理解

　　三、Prim和Kruscal算法

　　1.共同点：都是加权连通图里搜索最小生成树的算法。

　　2.不同点：prim算法是通过两个集合U,V-U，分别选择两个集合中的一个数，组成边信息，并选择最短的一条边。选择完后将V-U中被选择数删除，并加入到U集合中。直至U-V集合中不存在元素。

　　　　　　　kruscal算法是通过判断是否产生回路来选择边，若产生回路就将其舍弃，得出路径。

　　3.关于时间复杂度：记顶点数v，边数e
　　　　　　　(1)prim算法->邻接矩阵:O(v) 邻接表:O(elog2v)

　　　　　　　(2)kruscal算法->O(e^2)

　　四、Dijkstra算法

　　体会：Dijkstra算法是利用path数组记录上一路径，利用dist数组记录路径长度。并用两个集合S,U来记录已遍历的节点。在遍历过程中不断对path，dist数组进行修正得到最短路径。

　　在近期学的堆排列可以将此算法进行优化。

　　五、拓扑排序算法

　　1.执行步骤：

　　由AOV网构造拓扑序列的拓扑排序算法主要是循环执行以下两步，直到不存在入度为0的顶点为止。

　　(1) 选择一个入度为0的顶点并输出之；

　　(2) 从网中删除此顶点及所有出边。

　　循环结束后，若输出的顶点数小于网中的顶点数，则输出“有回路”信息，否则输出的顶点序列就是一种拓扑序列。

　　2.应用：判断是否存在回路（深度优先遍历也可以判断）

2.PTA实验作业（4分）

2.1 题目1：7-1 图着色问题

2.2 设计思路

void judge(MGraph &g)
{
定义整形变量： i用于记方案数,j和k用于遍历邻接矩阵,n为方案数

　　　　　　　　flag用于标记合法性，count用于记颜色数
定义整形数组： a[MAXV]存储颜色数据;
cin>>n;
for(i=0;i<n;i++)
{初始化flag=1，count=0；
　　for(j=1;j<=g.v;j++)
　　　　依次输入颜色值
　　for(k=1;k<=g.v&&flag!=0;k++)
　　{
　　　　for(j=1;j<=g.v&&flag!=0;j++)
　　　　{　　　若g.edges[k][j]不为0，说明相邻；
　　　　{　　　若对应的颜色数据a[k]==a[j]
　　　　　　　说明相邻节点颜色相同flag=0;
　　　　}
　　　　}
}
for(j=1;j<=g.v;j++)
　　for(k=j+1;k<=g.v;k++)
　　将a[]中的相同颜色数据其中一个赋值为-1：a[k]=-1;
　　for(j=1;j<=g.v;j++)
　　if(a[j]!=-1)
　　数组内无重复颜色，统计非-1的颜色数
　　若count与颜色数m不相同
　　　　说明存在问题flag=0;

　　根据flag的值输出Yes or No

}

2.3 代码截图

2.4 PTA提交列表说明。

1.前几次1分提交是采用了邻接表的存储结构，但是一直出现错误，并且检查修改多次没成效。思考后，发现采用邻接矩阵的存储在取节点数据的时候比较方便。所以修改成邻接矩阵后大部分都正确

2.20分和22分的提交问题在于，前者忽略了超过颜色数也是错误的方案。后者是题目理解问题，方案中采用的颜色数必须与题目所给的颜色数相同，小于颜色数也是错误的。

2.1 题目2：7-2 排座位

2.2 设计思路

void chaxun(MGraph &g)
{
定义整形变量：a,b为查询的两宾客,flag标记两敌对客人是否有共同朋友,i,j用于循环;

for(i=1;i<=g.m;i++)
{
　　cin>>a>>b;
　　若g.edges[a][b]==0说明客人间无关系

　　　　所以直接输出OK；
　　若g.edges[a][b]==1说明客人为朋友关系
　　　　所以直接输出No problem；
　　若g.edges[a][b]==-1说明客人为敌对关系
{
for(j=1;j<=g.v;j++)
{
初始化flag=0；
遍历整个邻接矩阵，若g.edges[j][a]==1&&g.edges[j][b]==1则说明客人之间有共同朋友
将flag置1;
通过判断flag是否非0

输出OK or OK but......
}

2.3 代码截图

2.4 PTA提交列表说明。

1.21的提交在最小规模出现的错误，思考后发现最小规模的特殊情况该算法未包含，调试后解决。

2.22分提交，目前依旧没解决最大N，全连通环，全查询的情况。

2.1 题目3：7-1 图着色问题

2.2 设计思路

全局变量：layer【】用于记录层数（距离第一个节点的距离）visited【】（用于记录节点是否访问过）

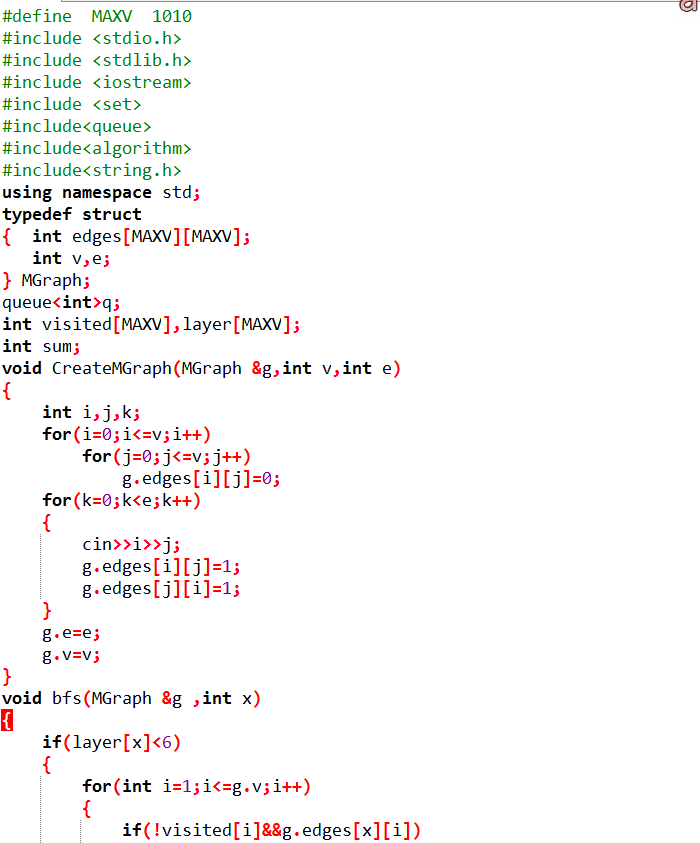
void bfs(MGraph &g ,int x)
{
　　若layer[x]<6 说明还未超过6层，执行
{
for(int i=1;i<=g.v;i++)
{
　　若节点未被访问过，且i，x节点连通
{
　　layer[i] 在layer[x]的基础上加上1层;
　　visited[i] 置1，标记为已访问节点;
　　节点总数sum++;
　　i入队

}
}
}
若队列不为空
{
　　取队顶元素，并删除该元素
　　递归bfs(g,x);
}
}

2.3 代码截图

2.4 PTA提交列表说明。

1.前几次的0分提交我采用了集合的递归算法，代码如下

但是尝试了多次始终错误，并且在测试过程中DEVC++出现直接跳出程序，无法输入的情况，无法解决问题。

2.前一次的答案正确是我复制网上查询的代码尝试是否正确。确认算法正确后，学习代码思想，采用了深度遍历的方法。

但是多次测试都是段错误，但把MAXV的范围缩小到1010后答案正确。

由此得出题目是有漏洞的，题目条件如下

所以MAXV的范围应该在10000+，但是在10000+的情况下出现段错误。因此题目存在漏洞