版权声明:本系列文章为博主原创文章,转载请注明出处!谢谢!
简介:本章是机器学习原理与算法系列博文的番外篇。。。
番外篇背景:
博主学习Machine Learning (CS229 powered by Standford)课程到第8课SVM的时候终于领悟到,之前碰到的很多算法,其实都是数学中的最优化问题。不幸的是,博主在本科和硕士阶段都没有上过最优化的课程。硕士期间学校要求至少选两门数学课,同学大部分都选了矩阵理论和最优化,而我当初别(nao)出(dai)心(chou)裁(jin)的选了矩阵理论和应用随机过程,因此优雅的错过了在机器学习领域甚为重要的一门课程。。。
博主已经意识到,如果能有一定的最优化理论知识基础,必然能极大地帮助理解课程中的大部分算法。因此,博主在这里强烈建议各位没有学习过最优化课程以及学习过但是都忘光光的诸君,在正式开始学习CS229之前,至少看完第3节。
本章索引:
1. 最优化问题概述
2. 函数等高线
3. 凸优化定义
4. 凸优化问题求解
1. 最优化问题概述
机器学习中的大多数问题可以归结为最优化问题。把一些典型的问题用最优化的方法建立数学模型,再最优化的方式求解。一般的优化问题定义和表示如下:
\begin{eqnarray*} min\ \ f_0(x) \qquad \qquad \\ s.t. \ \ f_i(x) \le 0, \ \ i=1,\cdots,m \\ h_i(x)=0,\ \ i=1,\cdots,p \end{eqnarray*}
其中$f_0(x)$是优化目标,也就是说,这个问题的最终目标是要找到一个$x$的值,使得$f_0(x)$取到最小值;那么在哪个范围内去找$x$呢? $s.t.$后面的两个式子就是约束x查找范围的,称作约束条件。 $f_i(x) \leq 0$称作不等式约束,方程组$h_i(x) = 0$称作等式约束。这两个约束都不是必须存在的,也可以只有一个,或者一个都没有。如果一个都没有,那么问题就变成了无约束问题。
2.函数等高线
在后续优化课程的学习中,将不断碰到函数等高线的概念,特别是梯度下降算法。博主以前也依稀接触过,但印象已经很模糊了,借着这个机会来温习下。由于我们用手来画三维图像很困难,我们可以用等高线图来描述图像会更加简单。等高线图用于描述两维输入和一维输出的函数,例如$f(x,y)=x^2+xy+y^2$。
本来三维函数的图像很复杂,如下图:
为了简化画图的流程故用等高线来表示。 把上图看做是一个一个的山包,现在我们用N把刀,分作N次,每次都从一个固定的高度把图上的山包做横切,得到的整个切面就是等高线。
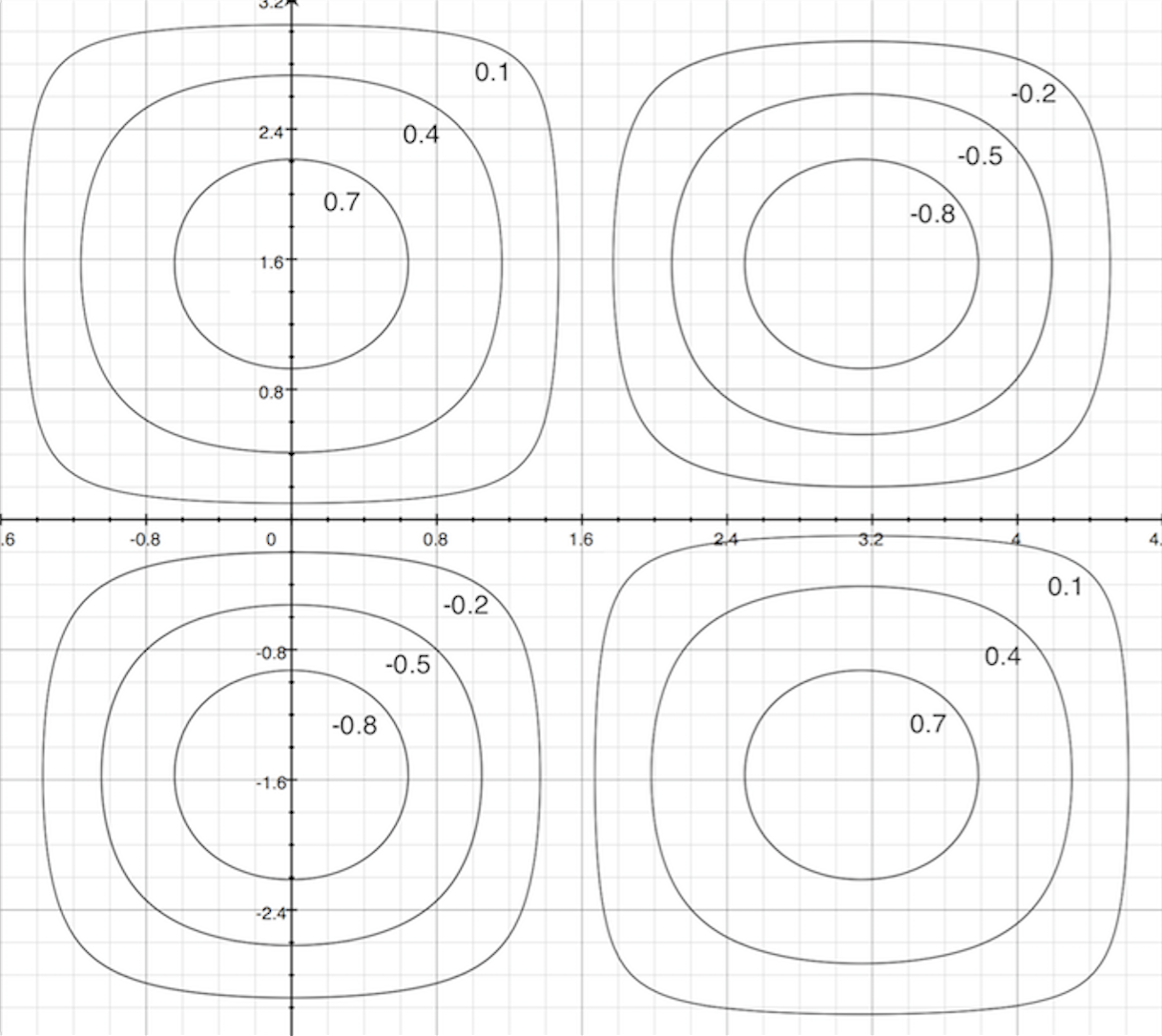
上图中,每一个圈都代表一个高度(高度其实就是函数的值$f(x,y)$)。圈与圈之间是等间隔的,因此,越密集的圈表示越陡峭,即函数值变化越快。我在这边不举具体的例子了,等用到的时候,回来一看就明白了。
3. 凸优化定义
在最优化的理论中,貌似凸优化是很特殊的算法?没错,就是很特殊。在查阅了大量的知乎后,终于从简书上找到了答案:
凸优化之所以如此重要,是因为:
1、其应用非常广泛,机器学习中很多优化问题都要通过凸优化来求解;
2、在非凸优化中,凸优化同样起到重要的作用,很多非凸优化问题,可以转化为凸优化问题来解决;
3、凸优化问题可以看作是具有成熟求解方法的问题,而其他优化问题则未必。
我们知道了凸优化很重要,而且算法很成熟,因此我们应当尽量把一般的优化问题向凸优化靠拢。凸优化的定义是什么呢?回顾第一节定义的一般优化问题,我们在此基础上再添加两个条件,那么一般优化问题就转化成了凸优化问题:
(1). 目标函数$f_0(x)$和不等式约束函数$f_i(x)$是凸函数。其中,凸函数的定义有很多种描述形式,最简单的一种是:如果一个函数的二阶导数大于等于零,那么这个函数就是凸函数。还有一种是Jensen不等式:$f(\frac{x+y}{2}) \le \frac{f(x)+f(y)}{2} $ <==> $f$是凸函数。线性函数、仿射函数、指数函数、范数、二次项系数为正的二次函数等,都是凸函数。这是凸函数在机器学习领域中的定义,在其他领域中可能有不同。
(2). 等式约束$h_i(x)$是仿射函数。所谓放射函数,就是最高次数为1的多项式函数。我们常见的线性函数(必须过原点)就是常数项为零的特殊仿射函数。
4. 凸优化问题求解
当一个问题确定为凸优化问题后,我们有很多种方法可以来求解,常用的方法包括梯度下降、牛顿法和拉格朗日乘数法等。这些问题在后续机器学习课程中都有讨论。



