Leetcode 373, Find K Pairs with smallest sums
You are given two integer arrays nums1 and nums2 sorted in ascending order and an integer k.
Define a pair (u,v) which consists of one element from the first array and one element from the second array.
Find the k pairs (u1,v1),(u2,v2) ...(uk,vk) with the smallest sums.
Example 1:
Given nums1 = [1,7,11], nums2 = [2,4,6], k = 3 Return: [1,2],[1,4],[1,6] The first 3 pairs are returned from the sequence: [1,2],[1,4],[1,6],[7,2],[7,4],[11,2],[7,6],[11,4],[11,6]
Example 2:
Given nums1 = [1,1,2], nums2 = [1,2,3], k = 2 Return: [1,1],[1,1] The first 2 pairs are returned from the sequence: [1,1],[1,1],[1,2],[2,1],[1,2],[2,2],[1,3],[1,3],[2,3]
Example 3:
Given nums1 = [1,2], nums2 = [3], k = 3 Return: [1,3],[2,3] All possible pairs are returned from the sequence: [1,3],[2,3]
本题的特点在于两个list nums1和nums2都是已经排序好的。本题如果把所有的(i, j)组合都排序出来,再取其中最小的K个。其实靠后的很多组合根本用不到,所以效率较低,会导致算法超时。为了简便,把nums1和nums2里面的元素写成A1,A2,...,A5, B1,...,B5. 维护一个最小堆。并逐渐往里面push and pop元素。
注意以下几点:1. 如果(Ai, Bj)大于堆顶的元素,那么没有必要把(Ai, Bj)和它之后的元素Push进堆。2. 为了便于管理,解法里其实只维护了一个指针idx2。如果 (A1,B[idx2])已经小于堆顶的元素,那么就把(A1,B[idx2]),...,(A5,B[idx2])全都推到堆里面。
第〇步,把一个最大元素放进堆。注意这一步很重要,否则可能会出现(A1,B2)大于所有(Ai,B1)的情况,也就是第二步中红色箭头大于蓝色箭头的情况始终不会出现,那么如果k足够大,就可能会出现pop一个空堆的bug。
第一步 把所有的(A1,B1),..., (A5,B1)推入堆。也就是把所有的黑色箭头连接的pair都放到堆里。
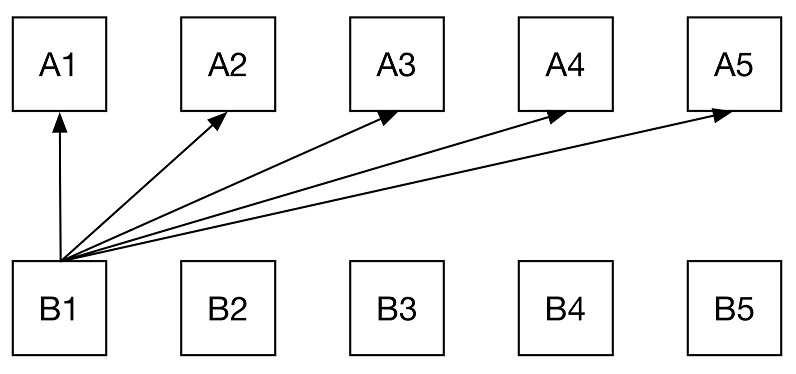
然后在逐个pop堆顶的元素。直到出现(A1,B2)小于堆顶的情况 (红色箭头小于蓝色箭头)。如果出现,把所有的(A1,B2),...,(A5,B2)放进堆。恢复pop堆顶元素,并且开始监视下一个红色箭头(A1,B3)是否小于堆顶的元素。
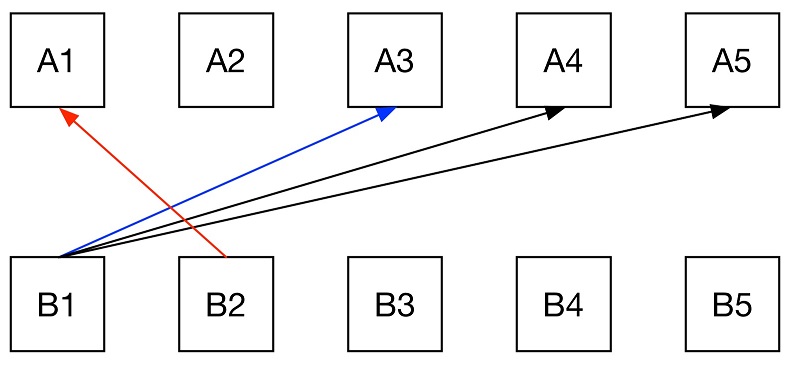
1 def kSmallestPairs(nums1, nums2, k): 2 """ 3 :type nums1: List[int] 4 :type nums2: List[int] 5 :type k: int 6 :rtype: List[List[int]] 7 """ 8 ans = [] 9 heap = [(0x7FFFFFFF, None, None)] 10 size1, size2 = len(nums1), len(nums2) 11 idx2 = 0 12 while len(ans) < min(k, size1 * size2): 13 if idx2 < size2: 14 sum, i, j = heap[0] 15 if nums2[idx2] + nums1[0] < sum: 16 for idx1 in range(size1): 17 heapq.heappush(heap, (nums1[idx1] + nums2[idx2], idx1, idx2)) 18 idx2 += 1 19 sum, i, j = heapq.heappop(heap) 20 ans.append((nums1[i], nums2[j])) 21 return ans



