网络流小记(EK&dinic&当前弧优化&费用流)
欢 迎 来 到 网 络 瘤 的 世 界
什么是网络流?
现在我们有一座水库,周围有n个村庄,每个村庄都需要水,所以会修水管(每个水管都有一定的容量,流过的水量不能超过容量)。最终水一定会流向唯一一个废水处理厂(至于为什么只有一个就不是我们能知道的了)。
最大流
神马是最大流?
要我们求能流向废水处理厂的最多的水量。
由于每个村庄的人都不想要水量过多导致爆掉水管结果水漫金村(雾),所以在水库到废水处理厂的一条路径流过的水量最多是这条路径上最小的水管容量。同时因为有不只一根水管和水库连接,所以水可以在多条路径上流。以及在各种物理因素下水不能倒流。
还是举个生动形象的栗子叭

其中水库是1,废水处理厂是6
最大流:
1--->3-->6 贡献流量:35
1-->2-->6 贡献流量:40
1--->4--->5--->6 贡献流量:30
1-->4-->3-->2-->6 贡献流量:10
1-->4-->3-->6 贡献流量:5
35+45+30+10+5=125
是不是流法很鬼畜?
那我们先来模拟一下找最大流的过程叭
在模拟之前先介绍点东西(大白话版本的定义\(ρωρ\)):
容量:这条边最多能流多少水
流量:这条边实际流了多少水
反向边:就是与原图的边方向相反的边辣。注意反向边的“容量”是正向边当前的流量
残量:正向边的容量-这条边上的残量
增广路:另一条能使得总流量更大的路径
从1出发,随便找一条路径
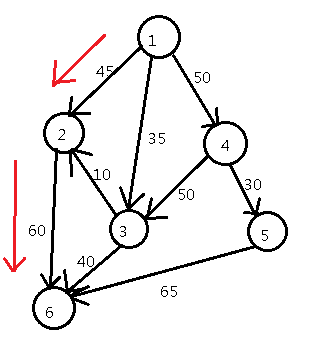
找到1-->2-->6这条路径,路径上的边的最小的容量是45,流满它,现在的流量是45,并且建反向边
路径上的边的流量减少45,所建的反向边的流量增加45
诶?反向边是干嘛的???别急,到后面就知道辣
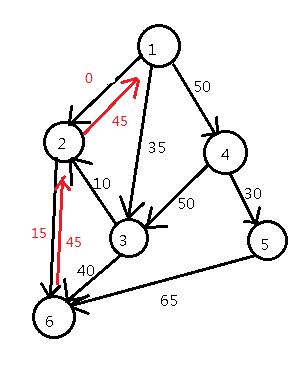
因为1-->2这条边的残量已经是0了,所以水就不能从这里流过去了。我们换一条能流的边
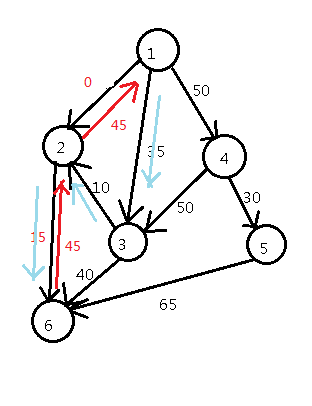
找到路径1--->3-->2-->6,总流量是55
同样进行建反向边的操作
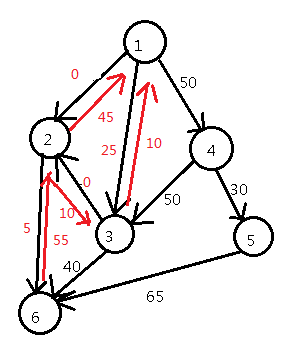
继续搞
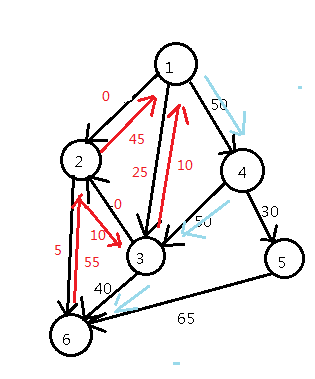
总流量:95
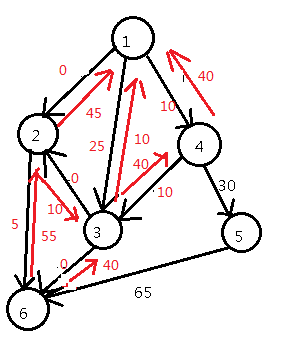
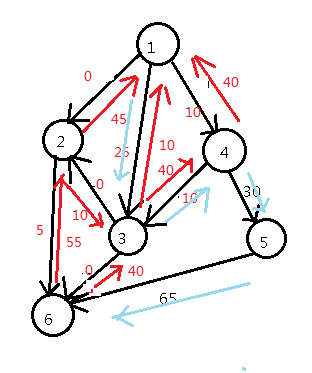
总流量:120

到了现在,只能走1--->4这条边了
总流量:125
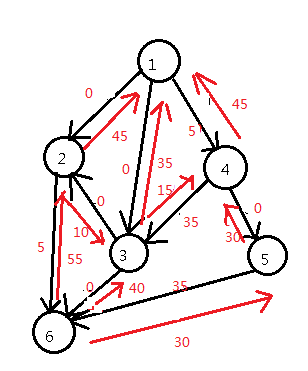
现在无法继续找出增广路,所以最大流为125
在上面的模拟过程中,注意到反向边也是可以走的,那么反向边到底有什么用呢?
感性李姐
反向边其实就是反悔标记,因为一下子就找出最优路径的可能性很低,我们要给自己留条后路。
注意到反向边的容量是正向边的流量。当路径上出现反向边的时候,反向边的容量减少,正向边的容量增加,就相当于把流量还给了正向边。在意义上,相当于你告诉之前找到的某条路径上的水,走反向边所到达的点会更优
可以看出来,跑最大流的核心是不断寻找增广路。在上面的模拟中,找不到增广路时的总流量就是最大流。
有关最大流的一些神奇的东西
1.最小割=最大流
什么是割?
给你一张图,让你去掉一些边,使得这张图分为不连通的两部分。去掉的所有边的边权之和就是割。
为什么最小割=最大流?不会证
个人的xjb证明:
如果把边权视为流量,则最大流保证从s到t的每一条路径上的有最小边权的那条边e的残量为0,最大流也是所有e的边权之和。而断开所有的e,也就是在s到t的所有路径上边权最小的边都被断开,s与t刚好不连通。此时所有e的边权之和就是一个割,又因为e是路径上边权最小的边,所以就是最小割。证毕。
2.二分图上的最大流=二分图最大匹配数(所有连边流量为1,建立超源超汇)
莫得证明
3.最短路径覆盖数=点数-二分图最大匹配数
看起来网络流很nb很有用的亚子,so我们怎么写粗来代码呢?
Dinic的最最最初版:\(EK\)
全名太长了没记住 \(Edmond\ Karp\),在XXXX年由Dinic提出(没错就是提出Dinic算法的这个人)
我们先来看看EK是怎么工作的。
在上面的模拟中,我们不断找增广路,直到没有为止。这也就是\(EK\)算法的思想。
通过BFS不断无脑找增广路就好辣
总之EK难写难用我们跳过
转自大神 乌克兰大野猪的代码
#include<iostream>
#include<stdio.h>
#include<queue>
#include<string.h>
using namespace std;
const int N = 205;
const int INF = 0x3f3f3f3f;
int c[N][N]; //记录i到j的剩余流量
int p[N]; //p[i]记录流向i点的前驱节点
int v[N]; //记录在一条增广路中,流到i点时,此刻增广路上残余量的最小值,直到i == m时就是整条增广路上的残余量最小值
int n, m;
int min(int a, int b){
return a <= b ? a : b;
}
void EK(){
//从1出发,不断找可以到达m的增广路
int ans = 0;
while(true){
//EK算法的核心是通过bfs不断查找增广路,同时建立反向弧
//每次循环都要对v数组和p数组进行清空,因为是意图查找一条新的增广路了
memset(p, 0, sizeof(p));
memset(v, 0, sizeof(v));
queue<int> q;
q.push(1);
v[1] = INF;
//每次只找一条增广路,同时修改c[i][j]的值
while(!q.empty()){
int f = q.front();
q.pop();
for(int i = 1; i <= m; i++){
if(v[i] == 0 && c[f][i] > 0){ //v[i]原本是记录增广路实时的残量最小值,v[i]==0代表这个点还没有走过,且从p到i的残量大于0说明通路
v[i] = min(v[f], c[f][i]); //实时更新v[i]的值,v[f]存储1条增广路中i点前所有水管残量的最小值,v[i]为该条增广路到i点为止,路径上的最小残量
p[i] = f; //p[i]实时保存i点的前驱节点,这样就当i==m时整条增广路就被记录下来
q.push(i); //将i点入队
}
}
}
if(v[m] == 0) break; //如果v[m]==0则代表找不到增广路了(中途出现了c[i][j]==0的情况)
ans += v[m];
int temp = m;
while(p[temp] != 0){ //类似并查集的查操作,不断查上一个元素且将剩余残量减去最小残联,反向弧增加最小残量
c[p[temp]][temp] -= v[m];
c[temp][p[temp]] += v[m];
temp = p[temp];
}
}
printf("%d\n", ans);
}
int main(){
while(scanf("%d%d", &n, &m) != EOF){
memset(c, 0, sizeof(c));
for(int i = 1; i <= n; i++){
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
c[x][y] += z; //初始时,从x流向y的剩余流量就是输入的值
}
EK();
}
return 0;
}
这个是自己调的+小部分处理借鉴lz大神的邻接表的代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
using namespace std;
inline int read()
{
char ch=getchar();
int x=0;bool f=0;
while(ch<'0'||ch>'9')
{
if(ch=='-')f=1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<3)+(x<<1)+(ch^48);
ch=getchar();
}
return f?-x:x;
}
int n,m,s,t,cnt=1,head[100009],ans,flow;
int vis[100009];
int par[100009];
const int inf=214748364;
queue<int> q;
struct E
{
int to,nxt,dis;
}ed[300009];
void add(int fr,int to,int dis)
{
cnt++;
ed[cnt].to=to;
ed[cnt].dis=dis;
ed[cnt].nxt=head[fr];
head[fr]=cnt;
}
bool bfs()
{
while(!q.empty())q.pop();//队列不清空害死人
memset(vis,0,sizeof(int)*(n+5));
memset(par,0,sizeof(int)*(m+5));
vis[s]=inf;
q.push(s);
while(!q.empty())
{
int u=q.front();
q.pop();
if(u==t)return 1;
for(int e=head[u];e;e=ed[e].nxt)
{
int v=ed[e].to;
if(!vis[v]&&ed[e].dis)
{
par[v]=e;//一个神奇的记录路线的方式
vis[v]=min(vis[u],ed[e].dis);//vis数组类似上面的v数组
q.push(v);
}
}
}
return 0;
}
void EK()
{
while(bfs())
{
int tmp=par[t];
while(tmp)
{
ed[tmp].dis-=vis[t];
ed[tmp^1].dis+=vis[t];
tmp=par[ed[tmp^1].to];//tmp^1就是tmp的反向边,通过反向边来找回起点
}
ans+=vis[t];
}
}
int main()
{
n=read();m=read();s=read();t=read();
for(int i=1;i<=m;i++)
{
int fr=read(),to=read(),dis=read();
add(fr,to,dis);add(to,fr,0);
}
EK();
printf("%d",ans);
}
\(EK\)模板题:洛谷P3376
(\(ps:\)要使用邻接表的EK,在洛谷数据面前EK表现良好)
\(EK\)看起来很简单的亚子\(QwQ\)
\(EK\)复杂度与容量有关
\(for\ example\)这种毒瘤图会让\(EK\)痛不欲生
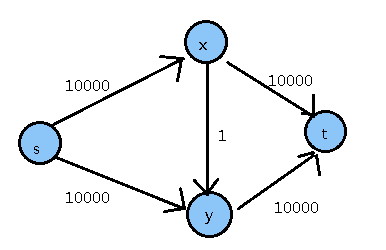
在这张图里,最坏情况下要跑20000次最大流,而最少只要2次
好吧实测并卡不了EK
复杂度和脸有关(这时候窝这个非酋就该哭了),运气不好运行时间就是运气好的2倍左右
我们当然想要稳一点的了
\(Dinic\)
\(EK\)需要欧气,那么对于非酋来说有没有一种更稳定的算法呢?
为了介绍Dinic让程序更快,\(Dinic\)引入了分层图的概念
莫得慌,这里的分层图不是改造路,飞行路线那种十分麻烦的分层图
这里的分层图,按照每个点到s的最短距离,分出每个点的深度,把同一深度的点分成一个组(当然代码里面不用分辣),就很像一层一层的。这就是\(Dinic\)里面的分层图。
深度先用bfs处理出来,然后按照深度进行dfs。强制当前点i只能dfs到比i深度多1的点。就会比EK快很多,稳很多
\(Dinic\)还有更秀的操作——————一次dfs实现多路增广
在dfs时,多传入一个参数in,表示传递到当前点的流量。如果找到了一条增广路,则in要减去这条增广路上贡献的流量,同时用out记录流出去的流量(out+=增广路贡献的流量),表示当前点有一些流量流出去了。当dfs回溯到当前点的时候,如果in不为0,则说明当前点还有剩余的没有流出去的流量,可以考虑继续找增广路。
一次dfs返回的是进行多路增广后,能流出去的最大流量(也就是out)
注意为了方便搞反向边,第一条边的编号是2
先来看看dfs的代码
int dfs(int u,int in)//in是当前点可以流出去的流量
{
if(u==t) return in;
int out=0;
for(register int e=head[u];e;e=ed[e].nxt)
{
int v=ed[e].to;
if(ed[e].dis&&dep[v]==dep[u]+1)
{
int ret=dfs(v,min(in,ed[e].dis));//要考虑每条边上容量的约束(当然dfs是先一条路走到黑)
ed[e].dis-=ret;//找到增广路后维护容量
ed[e^1].dis+=ret;
in-=ret;//流量流出去就没了,所以in要减去
out+=ret;//记录当前点流出去多少流量
if(in==0)return out;
}
}
return out;
}
感性李姐
好了接下来是全部代码
inline bool bfs()//看能否找到增广路&搞一下每个点的深度
{
bj=0;
memset(dep,0,sizeof(int)*(n+5+m));
dep[s]=1;
q.push(s);
while(!q.empty())
{
int u=q.front();
q.pop();
for(int e=head[u];e;e=ed[e].nxt)
{
int v=ed[e].to;
if(ed[e].dis&&!dep[v])//只有没有分配过深度的,且还能流过去水的点才考虑
{
dep[v]=dep[u]+1;
q.push(v);
}
}
if(u==t) bj=1;
}
return bj;
}
int dfs(int u,int in)
{
if(u==t) return in;
int out=0;
for(register int e=head[u];e;e=ed[e].nxt)
{
int v=ed[e].to;
if(ed[e].dis&&dep[v]==dep[u]+1)
{
int ret=dfs(v,min(in,ed[e].dis));
ed[e].dis-=ret;
ed[e^1].dis+=ret;
in-=ret;
out+=ret;
if(in==0)return out;
}
}
return out;
}
inline void dinic()
{
while(bfs())
{
ans+=dfs(s,200000000);//最开始的in是无限大(一般用2e9)
}
}
其实这个\(Dinic\)已经很\(nb\)了,但是它还可以变的更\(nb\)
秉着要刷最优解用时更少的心态,我们看看它还可以怎么优化
在dfs的时候,duliu出题人会给的一些十分恶心的图会出现这种情况:第x次dfs到一个点i,i有10000条边,但是前9999条边都流干了(dis值为0)。但是上面的程序还会把前9999条边再判断一次,从而导致if执行过多然后华丽的\(*TLE*\)
为了过掉duliu出题人给的图,我们可以用cur[i]记录下来每个点上一次循环到的边(显然cur[i]之前的边都流干了)。然后从cur[i]开始考虑每条边。
在bfs的时候,我们就把head数组备份一份到cur数组里,在dfs的时候进行更新
代码:
inline bool bfs()
{
bj=0;
memset(dep,0,sizeof(int)*(n+5+m));
for(int i=1;i<=n+m+5;i++)//注意初始化
cur[i]=head[i];
dep[s]=1;
q.push(s);
while(!q.empty())
{
int u=q.front();
q.pop();
for(int e=head[u];e;e=ed[e].nxt)
{
int v=ed[e].to;
if(ed[e].dis&&!dep[v])
{
dep[v]=dep[u]+1;
q.push(v);
}
}
if(u==t) bj=1;
}
return bj;
}
int dfs(int u,int in)
{
if(u==t) return in;
int out=0;
for(register int e=cur[u];e;e=ed[e].nxt)
{
cur[u]=e;//其实就是多加了个这个东西
int v=ed[e].to;
if(ed[e].dis&&dep[v]==dep[u]+1)
{
int ret=dfs(v,min(in,ed[e].dis));
ed[e].dis-=ret;
ed[e^1].dis+=ret;
in-=ret;
out+=ret;
if(in==0)return out;
}
}
return out;
}
int an;
inline void dinic()
{
while(bfs())
{
int ret=0;
while(ret=dfs(s,20000000)) ans+=ret;
}
}
费用流
神马又是费用流???
每条边又多了一项属性:单位费用
单位费用是干毛用的?
家里收水费484按照字收的?
单位费用就是一个字的价格
水流过这条边产生的费用就是单位费用\(\cdot\)流量
我们要做的就是在保证最大流的情况下,求出最小的费用
(据说这个东西叫做最小费用最大流,又名费用流)
咋求呢?
所有最大流中,一条可行流产生的费用=最大流\(\cdot\ \sum_{可行流经过的边i}边i的单位费用\)
那\(\sum_{可行流经过的边i}边i的费用\)越小,费用就越小
我们成功把问题转化成了在所有可行流中,找到单位费用最小的那一条流
显然这是个最短路
我们上面求最大流的程序显然不能记录下来所有最大流的可行流,所以我们考虑边求最大流边搞最短路
在上面的EK算法里面,通过不断bfs求最大流。这里我们可以采用类似EK的思想,不过是把bfs换成了spfa。用spfa更新当前找的这条增广路上的单位费用之和,同时记录最大流。因为找到最大流后,还得在经过的边上减去对应的流量(反向边是加),所以要记录路径。(记录路径的方式和邻接表的EK的记录方式一样)
诶spfa不是死了吗?为什么不用dij?因为在建反向边的时候,反向边的费用是负的,代表程序反悔了,把原来收的水费要回来了。出现了负边权,显然普通的dij跑不了
如果非要用dij,那么加个势(就是先对每条边加一个非常大的数,使所有边的边权为正,最后最短路再减去这个数)也是可以过的。但是我不会
发不哆嗦,来康康代码
const int inf=214748364;
int di[10009];//spfa用的dis数组(记录最短路)(为了~~少打一个字母~~不与其他的dis重叠,所以叫di)
int pre[10009];//记录当前找到的增广路的路径,pre[i]表示到点i的那条边
bool vis[10009];
ll liu,cost,flo[10009];//liu是最大流,cost是最小花费,flo[i]表示到点i的流量
struct E{
int to,nxt,dis,flow;//flow 是这条边的流量,dis是这条边的单位花费
}ed[2060100];//不要在意数组大小
//建边的函数懒得写了
inline bool spfa()
{
for(int i=1;i<=n;i++)
vis[i]=0,di[i]=inf;
//手动初始化大法好,memset害人不浅
vis[s]=1;di[s]=0;pre[t]=-1;
flo[s]=di[t];
q.push(s);
while(!q.empty())
{
int u=q.front();
q.pop();
vis[u]=0;
for(int e=head[u];e;e=ed[e].nxt)
{
int v=ed[e].to;
if(di[v]>di[u]+ed[e].dis&&ed[e].flow)
{
flo[v]=min((int)flo[u],ed[e].flow);
pre[v]=e;
di[v]=di[u]+ed[e].dis;
if(!vis[v])
{
vis[v]=1;
q.push(v);
}
}
}
}
return di[t]!=flo[s];//如果能够找到增广路就返回真
}
inline void MCMF()
{
while(spfa())
{
liu+=flo[t];//每次找增广路,flo[t]都是这条增广路贡献的流量,所以是liu+=flo[t],而不是liu=flo[t]
cost+=flo[t]*di[t];
int now=t;
while(now!=s)//一直回溯到起点
{
ed[pre[now]].flow-=flo[t];
ed[pre[now]^1].flow+=flo[t];
now=ed[pre[now]^1].to;//走反向边的终点,也就是这条边的起点,一直往前回溯
}
}
printf("%lld %lld",liu,cost);
}
鸣谢fzy神仙找错
\(QwQ\)



