机器学习：scipy和sklearn中普通最小二乘法与多项式回归的使用对

 

相关内容连接：

 机器学习：Python中如何使用最小二乘法(以下简称文一)

 机器学习:形如抛物线的散点图在python和R中的非线性回归拟合方法(以下简称文二)

     有些内容已经在上面两篇博文中提到了，所以就不重复了。这里主要讲的是sklearn包与scipy包中相关函数的区别。并且多项式回归和普通最小二乘法联系比较紧密，所以也放到此处讲了。

1.普通最小二乘法

   1）文一中的数据采用sklearn包的函数拟合    

from sklearn import linear_model
import numpy as np
import matplotlib.pyplot as plt

##样本数据(Xi,Yi)，需要转换成数组(列表)形式
Xi=np.array([6.19,2.51,7.29,7.01,5.7,2.66,3.98,2.5,9.1,4.2]).reshape(-1,1)
Yi=np.array([5.25,2.83,6.41,6.71,5.1,4.23,5.05,1.98,10.5,6.3]).reshape(-1,1)

##设置模型
model = linear_model.LinearRegression()
##训练数据
model.fit(Xi, Yi)
##用训练得出的模型预测数据
y_plot = model.predict(Xi)
##打印线性方程的权重
print(model.coef_) ## 0.90045842
##绘图
plt.scatter(Xi, Yi, color='red',label="样本数据",linewidth=2)
plt.plot(Xi, y_plot, color='green',label="拟合直线",linewidth=2)
plt.legend(loc='lower right')
plt.show()

   2）结果图

     

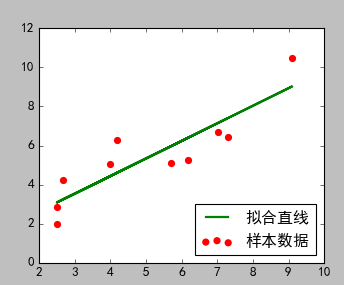
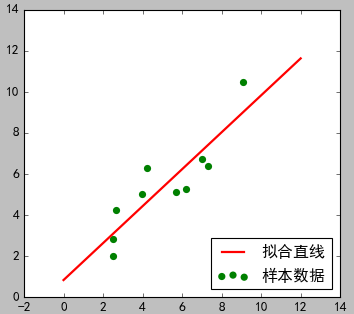
            （当前代码图）                                                   （文一图片）

    3）分析说明

          从结果看，两种方式的拟合结果相似。但是这里只有一个可知参数：0.90045842，而且拟合的线性方程具体形式未知。文一的方式可以自己设置线性方程形式，并且所有参数都可以求的结果。

 

2.多项式回归

      多项式回归其实是对普通最小二乘法的一个扩展，即当标准的直线方程(一元一次方程)无法满足拟合要求的时候，可以扩展到多元多次方程，例如文二中的例子就简单的扩展了一下：一元二次方程。

      下面要说的sklearn包中多项式回归的使用方式其实和文二中的方式一样：指定一个基函数，但是我查看了官网的大部分例子，发现只能使用sklearn包中的线性回归函数，无法像文二一样自定义基函数

      下面是使用例子：

from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge

##样本数据(Xi,Yi)，需要转换成数组(列表)形式
Xi=np.array([1,2,3,4,5,6]).reshape(-1,1)
#Yi=np.array([9,18,31,48,69,94])
Yi=np.array([9.1,18.3,32,47,69.5,94.8]).reshape(-1,1)
##这里指定使用岭回归作为基函数
model = make_pipeline(PolynomialFeatures(2), Ridge())
model.fit(Xi, Yi)
##根据模型预测结果
y_plot = model.predict(Xi)

##绘图
plt.scatter(Xi, Yi, color='red',label="样本数据",linewidth=2)
plt.plot(Xi, y_plot, color='green',label="拟合直线",linewidth=2)
plt.legend(loc='lower right')
plt.show()

       

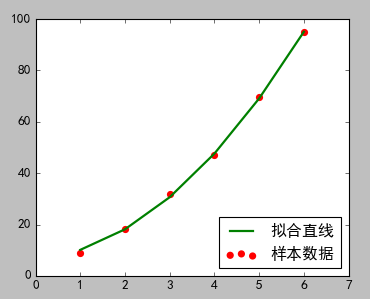
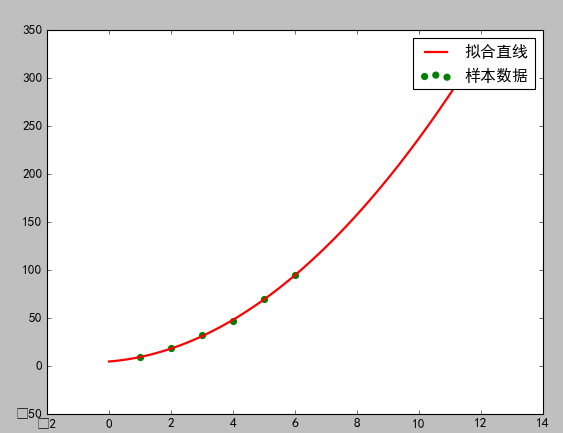
               （本例结果图）                                                              (文二图)

 

     在本例中完全得不到关于参数的任何信息。

 

3.总结

    1.多项式回归是线性模型的一个扩展 

    2.scipy包中关于最小二乘法或者多项式回归的使用方式比较方便灵活