机器学习:浅析使用二元决策树进行回归分析
1.引言
学过数据结构的同学对二叉树应该不陌生:二叉树是一个连通的无环图,每个节点最多有两个子树的树结构。如下图(一)就是一个深度k=3的二叉树。
(图一) (图二)
二元决策树与此类似。不过二元决策树是基于属性做一系列二元(是/否)决策。每次决策从下面的两种决策中选择一种,然后又会引出另外两种决策,依次类推直到叶子节点:即最终的结果。也可以理解为是对二叉树的遍历,或者很多层的if-else嵌套。
这里需要特别说明的是:二元决策树中的深度算法与二叉树中的深度算法是不一样的。二叉树的深度是指有多少层,而二元决策树的深度是指经过多少层计算。以上图(一)为例,二叉树的深度k=3,而在二元决策树中深度k=2。
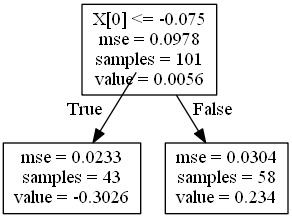
图二就是一个二元决策树的例子,其中最关键的是如何选择切割点:即X[0]<=-0.075中的-0.0751是如何选择出来的?
2.二元决策树切割点的选择
切割点的选择是二元决策树最核心的部分,其基本思路是:遍历所有数据,尝试每个数据作为分割点,并计算此时左右两侧的数据的离差平方和,并从中找到最小值,然后找到离差平方和最小时对应的数据,它就是最佳分割点。下面通过具体的代码讲解这一过程:
import numpy import matplotlib.pyplot as plot #建立一个100数据的测试集 nPoints = 100 #x的取值范围:-0.5~+0.5的nPoints等分 xPlot = [-0.5+1/nPoints*i for i in range(nPoints + 1)] #y值:在x的取值上加一定的随机值或者叫噪音数据 #设置随机数算法生成数据时的开始值,保证随机生成的数值一致 numpy.random.seed(1) ##随机生成宽度为0.1的标准正态分布的数值 ##上面的设置是为了保证numpy.random这步生成的数据一致 y = [s + numpy.random.normal(scale=0.1) for s in xPlot] #离差平方和列表 sumSSE = [] for i in range(1, len(xPlot)): #以xPlot[i]为界,分成左侧数据和右侧数据 lhList = list(xPlot[0:i]) rhList = list(xPlot[i:len(xPlot)]) #计算每侧的平均值 lhAvg = sum(lhList) / len(lhList) rhAvg = sum(rhList) / len(rhList) #计算每侧的离差平方和 lhSse = sum([(s - lhAvg) * (s - lhAvg) for s in lhList]) rhSse = sum([(s - rhAvg) * (s - rhAvg) for s in rhList]) #统计总的离差平方和,即误差和 sumSSE.append(lhSse + rhSse) ##找到最小的误差和 minSse = min(sumSSE) ##产生最小误差和时对应的数据索引 idxMin = sumSSE.index(minSse) ##打印切割点数据及切割点位置 print("切割点位置:"+str(idxMin)) ##49 print("切割点数据:"+str(xPlot[idxMin]))##-0.010000000000000009 ##绘制离差平方和随切割点变化而变化的曲线 plot.plot(range(1, len(xPlot)), sumSSE) plot.xlabel('Split Point Index') plot.ylabel('Sum Squared Error') plot.show()
3.使用二元决策树拟合数据
这里使用sklearn.tree.DecisionTreeRegressor函数。下面只显示了主要代码,数据生成部分同上:
from sklearn import tree from sklearn.tree import DecisionTreeRegressor ##使用二元决策树拟合数据:深度为1 ##说明numpy.array(xPlot).reshape(1, -1):这是传入参数的需要:list->narray simpleTree = DecisionTreeRegressor(max_depth=1) simpleTree.fit(numpy.array(xPlot).reshape(-1,1), numpy.array(y).reshape(-1,1)) ##读取训练后的预测数据 y_pred = simpleTree.predict(numpy.array(xPlot).reshape(-1,1)) ##绘图 plot.figure() plot.plot(xPlot, y, label='True y') plot.plot(xPlot, y_pred, label='Tree Prediction ', linestyle='--') plot.legend(bbox_to_anchor=(1,0.2)) plot.axis('tight') plot.xlabel('x') plot.ylabel('y') plot.show()
结果如下图:
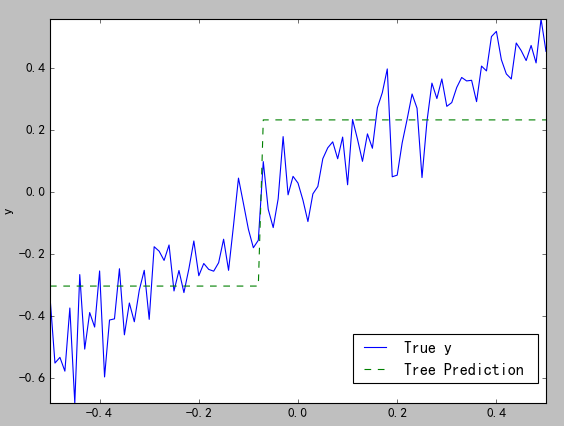
(图三)
当深度依次为2(图四)、深度为6(图5)时的结果:
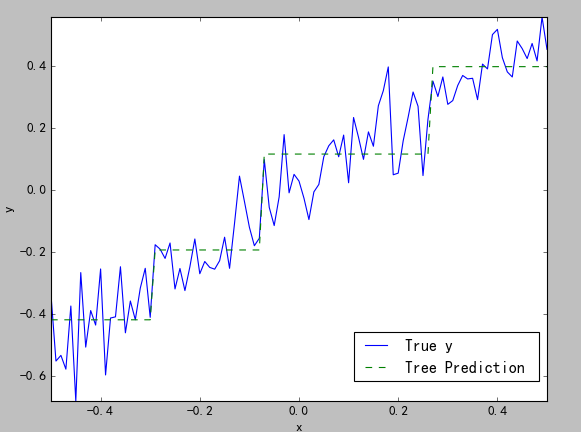
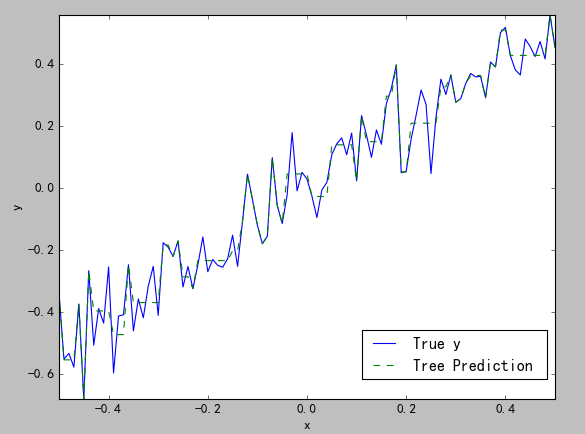
(图四) (图五)
4.二元决策树的过度拟合
二元决策树同普通最小二乘法一样,都存在拟合过度的情况,如图五所示,几乎看不到预测值的曲线,这就是拟合过度了。判断是否拟合过度有两种方法:
1)观察结果图。这个很好理解,就是直接看绘制的对比图。
2)比较决策树终止节点的数目与数据的规模。生产图五的曲线的深度是6(最深会有7层),即会有26=64个节点,而数据集中一共才有100个数据,也就是说有很多节点是只包括一个数据的。
5.二元决策树深度的选择
一般是通过不同深度二元决策树的交叉验证(前面已讲过原理)来确定最佳深度的,基本思路:
1)确定深度列表:
2)设置采用几折交叉验证
3)计算每折交叉验证时的样本外数据的均方误差
4)绘图,观察结果
下面就通过深度分别为1~7的10折交叉验证来检验下最佳深度。
import numpy import matplotlib.pyplot as plot from sklearn import tree from sklearn.tree import DecisionTreeRegressor #建立一个100数据的测试集 nPoints = 100 #x的取值范围:-0.5~+0.5的nPoints等分 xPlot = [-0.5+1/nPoints*i for i in range(nPoints + 1)] #y值:在x的取值上加一定的随机值或者叫噪音数据 #设置随机数算法生成数据时的开始值,保证随机生成的数值一致 numpy.random.seed(1) ##随机生成宽度为0.1的标准正态分布的数值 ##上面的设置是为了保证numpy.random这步生成的数据一致 y = [s + numpy.random.normal(scale=0.1) for s in xPlot] ##测试数据的长度 nrow = len(xPlot) ##设置二元决策树的深度列表 depthList = [1, 2, 3, 4, 5, 6, 7] ##每个深度下的离差平方和 xvalMSE = [] ##设置n折交叉验证 nxval = 10 ##外层循环:深度循环 for iDepth in depthList: ##每个深度下的样本外均方误差 oosErrors =0 ##内层循环:交叉验证循环 for ixval in range(nxval+1): #定义训练集和测试集标签 xTrain = [] #训练集 xTest = [] #测试集 yTrain = [] #训练集标签 yTest = [] #测试集标签 for a in range(nrow): ##如果采用a%ixval==0的方式写,会有除数为0的错误 if a%nxval != ixval%nxval: xTrain.append(xPlot[a]) yTrain.append(y[a]) else : xTest.append(xPlot[a]) yTest.append(y[a]) ##深度为max_depth=iDepth的训练 treeModel = DecisionTreeRegressor(max_depth=iDepth) ##转换参数类型 treeModel.fit(numpy.array(xTrain).reshape(-1, 1), numpy.array(yTrain).reshape(-1, 1)) ##读取预测值:使用测试集获取样本外误差 treePrediction = treeModel.predict(numpy.array(xTest).reshape(-1, 1)) ##离差列表:使用测试标签获取样本外误差 error = [yTest[r] - treePrediction[r] for r in range(len(yTest))] ##每个深度下的样本外均方误差和 oosErrors += sum([e * e for e in error]) #计算每个深度下的样本外平均离差平方和 mse = oosErrors/nrow ##添加到离差平方和列表 xvalMSE.append(mse) ##绘图---样本外离差和的平方平均值随深度变化的曲线 plot.plot(depthList, xvalMSE) plot.axis('tight') plot.xlabel('Tree Depth') plot.ylabel('Mean Squared Error') plot.show()
结果如图:
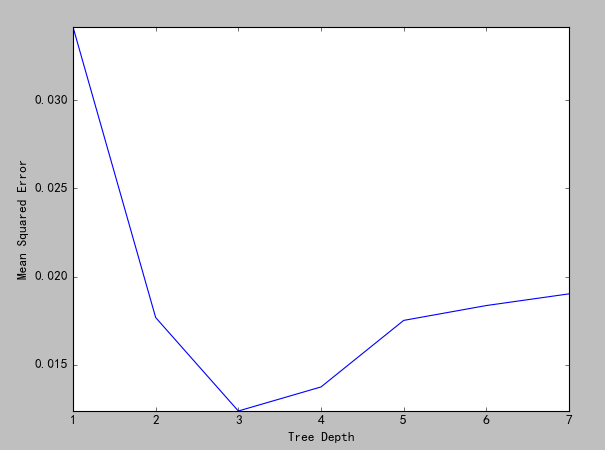
(图六)
从图中可以看出,当深度为3时的效果最好,下面我们把深度调成3,观察结果(为了效果调整了上面代码的颜色值):

(图七)


