机器学习:形如抛物线的散点图在python和R中的非线性回归拟合方法

   对于样本数据的散点图形如函数y=ax²+bx+c的图像的数据， 在python中的拟合过程为：

   

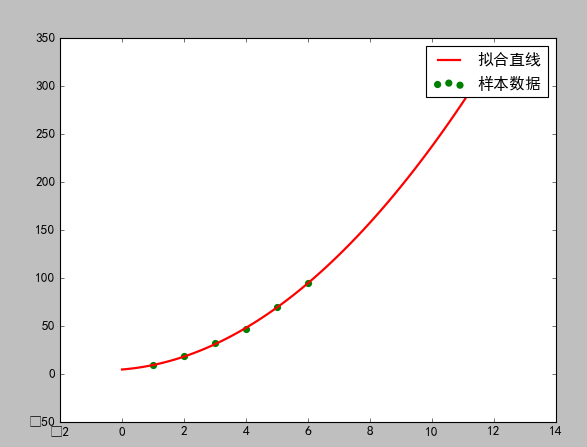
##最小二乘法
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
from scipy.optimize import leastsq

'''
     设置样本数据，真实数据需要在这里处理
'''
##样本数据(Xi,Yi)，需要转换成数组(列表)形式
Xi=np.array([1,2,3,4,5,6])
#Yi=np.array([9,18,31,48,69,94])
Yi=np.array([9.1,18.3,32,47,69.5,94.8])

'''
    设定拟合函数和偏差函数
    函数的形状确定过程：
    1.先画样本图像
    2.根据样本图像大致形状确定函数形式(直线、抛物线、正弦余弦等)
'''

##需要拟合的函数func :指定函数的形状
def func(p,x):
    a,b,c=p
    return a*x*x+b*x+c

##偏差函数：x,y都是列表:这里的x,y更上面的Xi,Yi中是一一对应的
def error(p,x,y):
    return func(p,x)-y

'''
    主要部分：附带部分说明
    1.leastsq函数的返回值tuple，第一个元素是求解结果，第二个是求解的代价值(个人理解)
    2.官网的原话（第二个值）：Value of the cost function at the solution
    3.实例：Para=>(array([ 0.61349535,  1.79409255]), 3)
    4.返回值元组中第一个值的数量跟需要求解的参数的数量一致
'''

#k,b的初始值，可以任意设定,经过几次试验，发现p0的值会影响cost的值：Para[1]
p0=[10,10,10]

#把error函数中除了p0以外的参数打包到args中(使用要求)
Para=leastsq(error,p0,args=(Xi,Yi))

#读取结果
a,b,c=Para[0]
print("a=",a,"b=",b,"c=",c)
print("cost："+str(Para[1]))
print("求解的拟合直线为:")
print("y="+str(round(a,2))+"x*x+"+str(round(b,2))+"x+"+str(c))

'''
   绘图，看拟合效果.
   matplotlib默认不支持中文，label设置中文的话需要另行设置
   如果报错，改成英文就可以
'''

#画样本点
plt.figure(figsize=(8,6)) ##指定图像比例： 8：6
plt.scatter(Xi,Yi,color="green",label="样本数据",linewidth=2) 

#画拟合直线
x=np.linspace(0,12,100) ##在0-15直接画100个连续点
y=a*x*x+b*x+c ##函数式
plt.plot(x,y,color="red",label="拟合直线",linewidth=2) 
plt.legend() #绘制图例
plt.show()

 运行结果：

 

a= 2.06607141425 b= 2.5975001036 c= 4.68999985496
cost：1
求解的拟合直线为:
y=2.07x*x+2.6x+4.68999985496

 

 

 在R中的拟合过程：（在控制台直接敲入或者放入脚本都可以）  

###设置函数形式
func<-function(a,b,c){
a*x*x+b*x+c
}
###设置样本数据
x<-c(1,2,3,4,5,6)
y<-c(9.1,18.3,32,47,69.5,94.8)
###把样本数据转换为符合nls函数需要的格式
d<-data.frame(y,x)
###执行求解过程：如果x,y值完全一一对应，汇报错误(循环次数超过了50这个最大值)
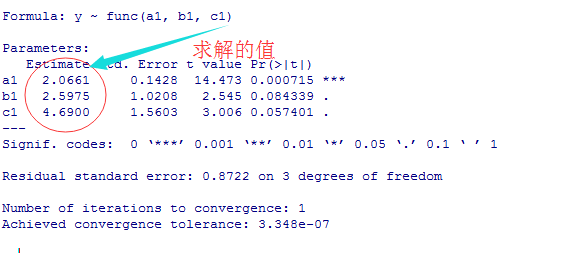
nlmod<-nls(y ~ func(a1,b1,c1),data=d,start=list(a1=1,b1=1,c1=1),trace=F)
###分析结果
summary(nlmod)

 运行结果：