leetcode解题笔记--part1--array
目录
18. 4Sum ★★
33. Search in Rotated Sorted Array ★
78. Subsets ★★
80. Remove Duplicates from Sorted Array II
81. Search in Rotated Sorted Array II ★
105. Construct Binary Tree from Preorder and Inorder Traversal ★★
106. Construct Binary Tree from Inorder and Postorder Traversal
152. Maximum Product Subarray ★★
153. Find Minimum in Rotated Sorted Array ★
209. Minimum Size Subarray Sum ★★
238. Product of Array Except Self ★
287. Find the Duplicate Number ★★
380. Insert Delete GetRandom O(1) ★
442. Find All Duplicates in an Array ★★
713. Subarray Product Less Than K ★
714. Best Time to Buy and Sell Stock with Transaction Fee ★★★
718. Maximum Length of Repeated Subarray
11.Container With Most Water【Medium】 返回目录
题目:


解题思路:
没有叫你返回具体坐标,只要求最大面积的话,那么用一个变量记录下,然后两边开始往中间移动
对于长边来讲,往里边移动一个坐标,无论更长或者更短,都不会使面积变大,所以每次都移动短边,这样每移动一次,最大面积都有可能更新
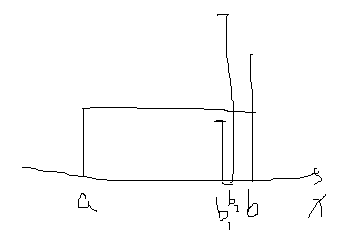
Tip:如果不采用两边移动的话,就是要进行两两遍历,也就是O(n2), 两边移动就是O(n)
code:
1 def maxArea(self, height): 2 """ 3 :type height: List[int] 4 :rtype: int 5 """ 6 i = 0 7 j = len(height)-1 8 maxarea = 0 9 while i < j: 10 maxarea = max((j-i)*min(height[i],height[j]), maxarea) 11 if height[i] < height[j]: 12 i += 1 13 else: 14 j -= 1 15 return maxarea
15. 3Sum【Medium】 返回目录
题目:
Given an array S of n integers, are there elements a, b, c in S such that a + b + c = 0? Find all unique triplets in the array which gives the sum of zero

解题思路:
做2Sum的时候用的是hash算法O(N)就可以做完,那么这个3Sum其实就是一个O(N)的2Sum, 于是乎就是O(N*N)的算法
2Sum算法如下:O(N)
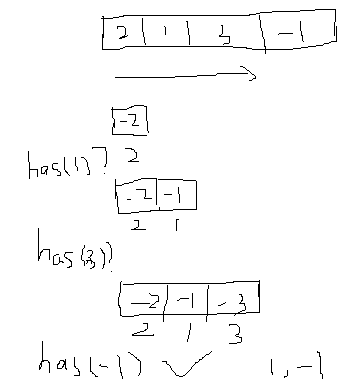
所以3Sum只需进行O(N)次2Sum就行了,写个循环完成
Tip:数组题要是涉及到找数字,记得用hash法,用空间换时间
code:
1 def threeSum(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: List[List[int]] 5 """ 6 length = len(nums) 7 if length < 3: 8 return [] 9 result = [] 10 nums.sort() 11 for i in range(length-2): 12 if i>0 and nums[i]==nums[i-1]: 13 continue 14 hash_table = {} 15 res = 0-nums[i] 16 for j in range(i+1,len(nums)): 17 if j>3 and nums[j]==nums[j-3]: 18 continue 19 if nums[j] in hash_table: 20 result.append([nums[i],res-nums[j],nums[j]]) 21 hash_table.pop(nums[j]) 22 else: 23 hash_table[res-nums[j]] = nums[j] 24 return result
哇,这道题处理重复很头疼啊,对于[1,0,-1,1]结果为[[1,0,-1],[0,-1,1]]显示说答案错误
如果找到一组解的时候,在result里面查询是否已经存在的话就会多一层循环,结果会超时。
所以这里预先将数组进行排序,让可行的结果呈顺序状,更好地防止结果重复。
但是面对大量重复数字的时候,出现很多问题, 比如[0,0,0,0,0,0,0,0,0,0,0,0], [-4,2,2,2,2,2,2,2,3]
这里就要求固定第一个数字的时候,希望不重复,也就是要跳过nums[i]==nums[i-1]的情况
对于第二个数字呢,因为只要求2sum,所以对于重复大于3的情况不需要考虑。即跳过nums[j]==nums[j-3]
很奇怪为什么我的算法ac时间很长,统计数据只打败了2.9%提交的python代码,看下别人的解法
code_writen_by_others:
1 def threeSum(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: List[List[int]] 5 """ 6 length = len(nums) 7 if length < 3: 8 return [] 9 result = [] 10 nums.sort() 11 for i in range(length-2): 12 if i>0 and nums[i]==nums[i-1]: 13 continue 14 res = 0 - nums[i] 15 low = i+1 16 high = length-1 17 while(low < high): 18 if(nums[low]+nums[high]==res): 19 result.append([nums[i],nums[low],nums[high]]) 20 while(low<high and nums[low]==nums[low+1]): 21 low += 1 22 while(low<high and nums[high]==nums[high-1]): 23 high -= 1 24 low +=1 25 high -=1 26 else: 27 if(nums[low]+nums[high]<res): 28 low += 1 29 else: 30 high -= 1 31 return result
我好笨啊,因为已经排好序了,所以没必要用hash,直接两头做加法往中间移动,比hash省了空间还省了时间
但是2Sum用hash更好,因为排序算法是O(NlogN)的,hash是O(N)的,所以追求效率的话还是hash
16. 3Sum Closest【Medium】 返回目录
题目:

解题思路:
与15题类似,只不过需要一个额外的哨兵记录下与目标的差异,遍历完留下差异最小的值
同时在遍历的过程中,如果比target要更大,需要移动更大的数变小,如果比target更小,需要移动更小的数变大
Tips:如果算法的时间复杂度为O(N*N), 那么最好事先就先排序,排好序之后就没有必要hash了,本来两头遍历复杂度也为O(N)
code:
1 def threeSumClosest(self, nums, target): 2 """ 3 :type nums: List[int] 4 :type target: int 5 :rtype: int 6 """ 7 nums.sort() 8 min_diff = float("inf") 9 for i in range(len(nums)): 10 res = target-nums[i] 11 low,high = i+1,len(nums)-1 12 while low < high: 13 diff = nums[low]+nums[high]-res 14 if diff == 0: 15 return target 16 if abs(diff) < min_diff: 17 min_diff = abs(diff) 18 result = nums[i]+nums[low]+nums[high] 19 if diff > 0: 20 high -= 1 21 else: 22 low += 1 23 return result
18. 4Sum【Medium】 返回目录
题目:

解题思路:
在网上看了一个特别brilliant的解法,让人觉得代码很有美感,而且还非常高效,就是把所有不需要的测试全部略过,让人赞叹不已
而且这道题还结合了前几道题的操作,这道题必须mark上两颗星
Tips:去除一些不必要的操作,虽然时间复杂度没有变,但是实际运行时间是减少的
code:
1 def fourSum(self, nums, target): 2 """ 3 :type nums: List[int] 4 :type target: int 5 :rtype: List[List[int]] 6 """ 7 nums.sort() 8 res = [] 9 if len(nums)<4 or 4*nums[0]>target or 4*nums[-1]<target: 10 return res 11 for i in range(len(nums)): 12 if i>0 and nums[i]==nums[i-1]: 13 continue 14 if nums[i] + 3*nums[-1] < target: 15 continue 16 if 4*nums[i] > target: 17 break 18 if 4*nums[i] == target: 19 if i+3<len(nums) and nums[i+3]==nums[i]: 20 res.append([nums[i],nums[i],nums[i],nums[i]]) 21 break 22 res.extend(self.threeSum(nums[i+1:],target-nums[i],nums[i])) 23 return res 24 25 def threeSum(self,nums,target,a): 26 res = [] 27 if len(nums)<3 or 3*nums[0]>target or 3*nums[-1]<target: 28 return res 29 for i in range(len(nums)): 30 if i>0 and nums[i]==nums[i-1]: 31 continue 32 if nums[i] + 2*nums[-1] < target: 33 continue 34 if 3*nums[i] > target: 35 break 36 if 3*nums[i] == target: 37 if i+2<len(nums) and nums[i+2] == nums[i]: 38 res.append([a,nums[i],nums[i],nums[i]]) 39 break 40 res.extend(self.twoSum(nums[i+1:],target-nums[i],a,nums[i])) 41 return res 42 43 def twoSum(self,nums,target,a,b): 44 res = [] 45 if len(nums)<2 or 2*nums[0]>target or 2*nums[-1]<target: 46 return res 47 i,j = 0,len(nums)-1 48 while i<j: 49 sum_temp = nums[i]+nums[j] 50 if sum_temp == target: 51 res.append([a,b,nums[i],nums[j]]) 52 i += 1 53 j -= 1 54 elif sum_temp > target: 55 j -= 1 56 else: 57 i += 1 58 while i>0 and i<len(nums) and nums[i]==nums[i-1]: 59 i += 1 60 while j>0 and j<len(nums)-1 and nums[j]==nums[j+1]: 61 j -= 1 62 return res
31. Next Permutation【Medium】 返回目录
题目:
给你一个排列,要你求出,作为全排列组合中它的下一个排列。一般都是指一个升序数列的全排列An^n个,比如说:
[1,2,3] --> [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] --> [1,2,3]
本题要求:找到给出排列的下一个排列


解题思路:
观察找到全排列的规律,发现是个多重循环,按位置从小到大,可以得到的规律如下:【借鉴别人给出的例子,侵删】
1 2 7 4 3 1 --> 1 3 1 2 4 7
从末尾往前看,数字逐渐变大,找到第一个开始变小的数字,也就是2
1 2 7 4 3 1 然后从后面往前找到第一个大于2的数字,也就是3,这里是想说第二个位置2后面的已经全排列完了,可以换成3了
1 3 7 4 2 1 换成三后面的又要重新进行全排列,全排列最后一个是逆序,第一个是顺序,所以只需要将3后面的翻转一下就可以
1 3 1 2 4 7
code:
1 def nextPermutation(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: void Do not return anything, modify nums in-place instead. 5 """ 6 a = -1 7 for i in range(len(nums)-1,0,-1): 8 if nums[i] > nums[i-1]: 9 a = i-1 10 break 11 if a==-1: 12 return nums.reverse() 13 b = a+1 14 for j in range(len(nums)-1,a,-1): 15 if nums[j]>nums[a]: 16 b = j 17 break 18 nums[a],nums[b] = nums[b],nums[a] 19 i,j = a+1,len(nums)-1 20 while i<j: 21 nums[i],nums[j] = nums[j],nums[i] 22 i += 1 23 j -= 1
33. Search in Rotated Sorted Array【Medium】 返回目录
题目:

就是说给定的数组是由一个升序数组就某个点翻转得到的,然后要在这样一个数组中查找某个数字,返回下标
解题思路:
直接暴力搜索,O(N) 我以为会超时,结果Accepted 可以没有利用到给定数组的特性,如果是升序数组的话可以用二分法是O(logN), 所以可以设计一个改进版二分法来处理这个问题
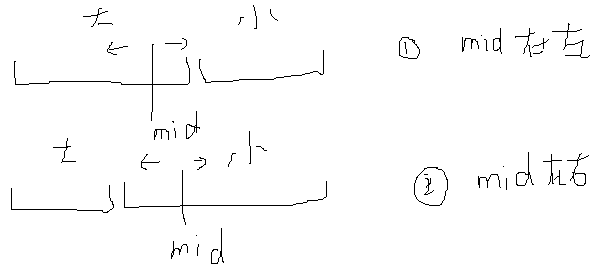
分两种情况:
a)mid如果在左边 : target在mid左 high=mid-1 target在mid右 low=mid+1
b)mid如果在右边 : target在mid左 high=mid-1 target在mid右 low=mid+1
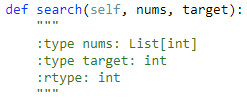
code:(暴力法) beat 16.87%
1 def search(self, nums, target): 2 """ 3 :type nums: List[int] 4 :type target: int 5 :rtype: int 6 """ 7 for i in range(len(nums)): 8 if nums[i] == target: 9 return i 10 return -1
code:(改进二分法) beat 25.32%
1 def search(self, nums, target): 2 """ 3 :type nums: List[int] 4 :type target: int 5 :rtype: int 6 """ 7 if len(nums) < 1: 8 return -1 9 low,high = 0, len(nums)-1 10 while(low<high): 11 mid = (low + high) // 2 12 if nums[mid] == target: 13 return mid 14 if nums[low] <= nums[mid]: 15 if target >= nums[low] and target < nums[mid]: 16 high = mid - 1 17 else: 18 low = mid + 1 19 else: 20 if target > nums[mid] and target <= nums[high]: 21 low = mid + 1 22 else: 23 high = mid -1 24 if nums[low] == target: 25 return low 26 else: 27 return -1
34. Search for a Range 【Medium】 返回目录
题目:

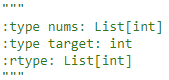
解题思路:
要求在O(logn)时间内,那么就是希望我们用二分法进行查找,首先先用二分法找到相应的值,然后再向左判断边界,再向右判断边界,向左向右的过程中都是使用二分法
code: beat 21.43%
1 def searchRange(self, nums, target): 2 """ 3 :type nums: List[int] 4 :type target: int 5 :rtype: List[int] 6 """ 7 if len(nums) < 1: 8 return [-1,-1] 9 low,high = 0,len(nums)-1 10 if nums[0]>target or nums[-1]<target: 11 return [-1,-1] 12 while(low <= high): 13 mid = (low+high)//2 14 if nums[mid] < target: 15 low = mid + 1 16 elif nums[mid] == target: 17 b = mid 18 high = mid - 1 19 else: 20 high = mid - 1 21 if nums[high+1] != target: 22 return [-1,-1] 23 a = high+1 24 high = len(nums)-1 25 while(low <= high): 26 mid = (low+high)//2 27 if nums[mid] > target: 28 high = mid - 1 29 else: 30 low = mid + 1 31 return [a,low-1]
39. Combination Sum 【Medium】 返回目录
题目:

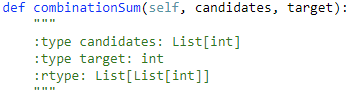
解题思路:
搜索+回溯 这道题很经典,理清楚怎么递归和回溯很重要
主要思路就是先第一个数字,再递归的求target-第一个数字,可以的话继续递归,不可以就回溯
我发现我真是有点笨,经常想不通怎么回溯
dfs的算法一定要非常熟悉,在python中通常都是要把path和result作为参数传入dfs函数中,用以记录可行的结果
Tips:求所有可能的解的时候就要想到搜索和递归
code: 参考的别人写的代码 beat 69.7% (大神就是厉害)
1 def combinationSum(self, candidates, target): 2 """ 3 :type candidates: List[int] 4 :type target: int 5 :rtype: List[List[int]] 6 """ 7 res = [] 8 self.dfs(candidates,target,0,[],res) 9 return res 10 def dfs(self,nums,target,index,path,res): 11 if target<0: 12 return 13 elif target==0: 14 res.append(path) 15 return 16 else: 17 for i in range(index,len(nums)): 18 self.dfs(nums,target-nums[i],i,path+[nums[i]],res)
上面的是递归回溯,下面是栈回溯
code: beat 68.18%
1 def combinationSum(self, candidates, target): 2 """ 3 :type candidates: List[int] 4 :type target: int 5 :rtype: List[List[int]] 6 """ 7 res = [] 8 self.dfs(candidates,target,0,[],res) 9 return res 10 def dfs(self,nums,target,index,path,res): 11 if target<0: 12 return 13 elif target==0: 14 res.append(path[:]) 15 return 16 else: 17 for i in range(index,len(nums)): 18 path.append(nums[i]) 19 self.dfs(nums,target-nums[i],i,path,res) 20 path.pop()
而且我今天还对python中的赋值机制进行了深入的学习,起因是第14行代码 如果直接写成 res.append(path)的话,后面修改path是在原地址上修改,起不到保存结果的作用,所以用path[:]切片操作,相当于创建了一个新的对象进行保存,就可以让代码正常运行了
学习链接是: https://my.oschina.net/leejun2005/blog/145911 这个博客解释得相当清楚
40. Combination Sum II 【Medium】 返回目录
题目: 同39 只是要求一个数只能用一次,所以只是循环的时候要求index+1,具体细节看39题
code: beat 73.81%
1 def combinationSum2(self, candidates, target): 2 """ 3 :type candidates: List[int] 4 :type target: int 5 :rtype: List[List[int]] 6 """ 7 res = [] 8 candidates.sort() 9 print(candidates) 10 self.dfs(candidates,target,[],0,res) 11 return res 12 def dfs(self,nums,target,path,index,res): 13 if target<0: 14 return 15 elif target==0: 16 res.append(path) 17 return 18 else: 19 for i in range(index,len(nums)): 20 if i>index and nums[i]==nums[i-1]: 21 continue 22 self.dfs(nums,target-nums[i],path+[nums[i]],i+1,res)
48. Rotate Image 【Medium】 返回目录
题目:
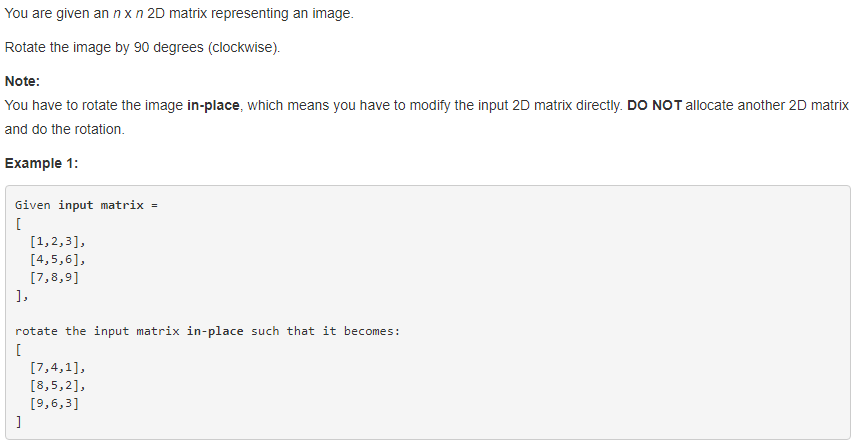

解题思路:
主要是寻找旋转前和旋转后坐标位置的对应关系,我们发现

所以就是对每一个正方形框的上边进行逐个元素的旋转置位,就可以了
code: beat 70.69% 完全自己写的,好有成就感哈哈哈~
1 def rotate(self, matrix): 2 """ 3 :type matrix: List[List[int]] 4 :rtype: void Do not return anything, modify matrix in-place instead. 5 """ 6 n = len(matrix)-1 7 for i in range(n//2+1): 8 for j in range(n-2*i): 9 matrix[i][i+j],matrix[i+j][n-i],matrix[n-i][n-i-j],matrix[n-i-j][i] = matrix[n-i-j][i],matrix[i][i+j],matrix[i+j][n-i],matrix[n-i][n-i-j]
然后看了下别人的解法
code: 比我的解法简单太多了,膜拜大神
1 def rotate(self, matrix): 2 """ 3 :type matrix: List[List[int]] 4 :rtype: void Do not return anything, modify matrix in-place instead. 5 """ 6 ''' 7 clockwise rotate 8 first reverse up to down, then swap the symmetry 9 1 2 3 7 8 9 7 4 1 10 4 5 6 => 4 5 6 => 8 5 2 11 7 8 9 1 2 3 9 6 3 12 ''' 13 matrix.reverse() 14 n = len(matrix) 15 for i in range(n-1): 16 for j in range(i+1,n): 17 matrix[i][j],matrix[j][i] = matrix[j][i],matrix[i][j]
54. Spiral Matrix【Medium】 返回目录
题目:把矩阵螺旋展开,不一定是方阵

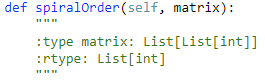
解题思路:
每个回路都对四条边进行遍历,坐标规律自己找,就是需要考虑好多情况,代码时完全debug出来的
code: beat 87%
1 def spiralOrder(self, matrix): 2 """ 3 :type matrix: List[List[int]] 4 :rtype: List[int] 5 """ 6 res = [] 7 if not len(matrix): 8 return [] 9 h,w = len(matrix),len(matrix[0]) 10 if not w: 11 return [] 12 n = (min(h,w)-1)//2 13 for i in range(n+1): 14 for j in range(w): 15 res.append(matrix[i][i+j]) 16 if h-1: 17 for j in range(1,h): 18 res.append(matrix[i+j][i+w-1]) 19 if h-1 and w-1: 20 for j in range(1,w): 21 res.append(matrix[i+h-1][i+w-j-1]) 22 if w-1 and h-1: 23 for j in range(1,h-1): 24 res.append(matrix[i+h-j-1][i]) 25 h -= 2 26 w -= 2 27 return res
参考别人的代码,我发现我想的太过于复杂或者说细节要考虑的太多,导致需要大量时间调试,舍本求末,其实很简单,只需要colbegin<=colend and rowbegin<=rowend这一个限制条件就可以了,没必要对所有的坐标特点都清楚
Tips:如果对于矩阵中的遍历,清楚地知道begin and end那么就没有必要知道i,j的变化细节
code:
1 def spiralOrder(self, matrix): 2 """ 3 :type matrix: List[List[int]] 4 :rtype: List[int] 5 """ 6 if not len(matrix): 7 return [] 8 if not len(matrix[0]): 9 return [] 10 res = [] 11 rowbegin,rowend = 0,len(matrix)-1 12 colbegin,colend = 0,len(matrix[0])-1 13 while(rowbegin<=rowend and colbegin<=colend): 14 for j in range(colbegin,colend+1): 15 res.append(matrix[rowbegin][j]) 16 rowbegin += 1 17 for j in range(rowbegin,rowend+1): 18 res.append(matrix[j][colend]) 19 colend -= 1 20 if rowbegin<=rowend: 21 for j in range(colend,colbegin-1,-1): 22 res.append(matrix[rowend][j]) 23 rowend -=1 24 if colbegin<=colend: 25 for j in range(rowend,rowbegin-1,-1): 26 res.append(matrix[j][colbegin]) 27 colbegin += 1 28 return res
注意,当遍历到下边和左边的时候,要进行判断,是否满足还可以遍历的条件
55. Jump Game 【Medium】 返回目录
题目:


解题思路:
我看到这个题目,第一眼就想到用递归深搜去做,结果直接超时,因为这个分支太多,用dfs适合那种分支较少的题目,比如说 39 ,像这种比较多情况的容易重复计算的题目就适合用动态规划做,这样就可以节省时间
动态规划的题最大的点就是要找到最优子结构:
for i in range(1,nums[i]):
dp[index] += dp[i]
如果用递归的话,dp[i]要被反复计算, 用动态规划的话,dp[i]只需要计算一次然后记录下来,整个过程应该是倒着来的
Tips:如果发现递归会有很多重复的求解,那么就改成动态规划
code:
我的超时解法:
1 def canJump(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: bool 5 """ 6 dp = nums[:] 7 dp[len(nums)-1] = True 8 for i in range(len(nums)-2,-1,-1): 9 dp[i] = False 10 for j in range(i+1,i+nums[i]+1): 11 if dp[j]: 12 dp[i] = True 13 break 14 return dp[0]
然后看别人的解法,发现,没有必要对每个点可以到达的地方都进行遍历,只需要对最大能到达的地方进行记录,当最大能到达的地方大于终点说明就能到达终点
code:
1 def canJump(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: bool 5 """ 6 i = 0 7 reach = 0 8 for i in range(len(nums)): 9 if i>reach: 10 break 11 reach = max(i+nums[i],reach) 12 return reach>=len(nums)-1
56. Merge Intervals【Medium】 返回目录
题目:
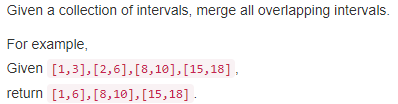
解题思路:
本来想用初中学的数轴法,也就是用一个flag记录是否需要覆盖,可是发现数轴法不适用,所以还是先排序,再遍历吧
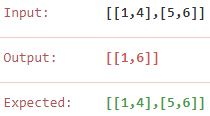
code: 数轴法[wrong error]
1 # Definition for an interval. 2 # class Interval: 3 # def __init__(self, s=0, e=0): 4 # self.start = s 5 # self.end = e 6 7 class Solution: 8 def merge(self, intervals): 9 """ 10 :type intervals: List[Interval] 11 :rtype: List[Interval] 12 """ 13 flag = [] 14 for i in range(len(intervals)): 15 for j in range(len(flag),intervals[i].start): 16 flag.append(0) 17 end = min(intervals[i].end+1,len(flag)) 18 for j in range(intervals[i].start,end): 19 flag[j] = 1 20 for j in range(end,intervals[i].end+1): 21 flag.append(1) 22 res = [] 23 i = 0 24 while i<len(flag): 25 if flag[i]: 26 temp = Interval(s=i) 27 while i<len(flag) and flag[i]: 28 i += 1 29 temp.end = i-1 30 res.append(temp) 31 else: 32 i += 1 33 return res 34
code: Accepted
1 # Definition for an interval. 2 # class Interval: 3 # def __init__(self, s=0, e=0): 4 # self.start = s 5 # self.end = e 6 7 class Solution: 8 def merge(self, intervals): 9 """ 10 :type intervals: List[Interval] 11 :rtype: List[Interval] 12 """ 13 if not intervals: 14 return [] 15 intervals.sort(key=self.getKey) 16 temp = intervals[0] 17 res = [] 18 for i in range(1,len(intervals)): 19 if intervals[i].start<=temp.end: 20 temp.end = max(intervals[i].end,temp.end) 21 else: 22 res.append(temp) 23 temp = intervals[i] 24 res.append(temp) 25 return res 26 27 def getKey(self, interval): 28 return interval.start
学会了结构体排序的方法 sorted(intervals, key=lambda i: i.start) list.sort(intervals, key=lambda i: i.start) 或者写成显示的函数
59. Spiral Matrix II 【Medium】 返回目录
题目:
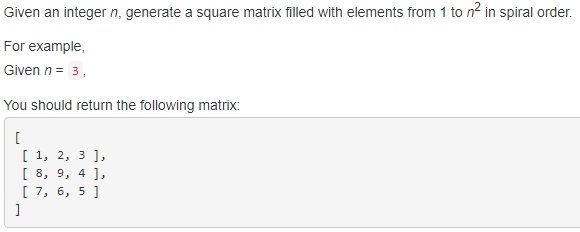
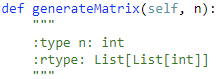
解题思路:
同 54 题, 使用的是第二种解法
code:
1 def generateMatrix(self, n): 2 """ 3 :type n: int 4 :rtype: List[List[int]] 5 """ 6 rowbegin = colbegin = 0 7 rowend = colend = n-1 8 res = [ [ 0 for i in range(n) ] for j in range(n) ] 9 count = 1 10 while rowbegin <= rowend and colbegin <= colend: 11 for i in range(colbegin,colend+1): 12 res[rowbegin][i] = count 13 count += 1 14 rowbegin += 1 15 for i in range(rowbegin,rowend+1): 16 res[i][colend] = count 17 count += 1 18 colend -= 1 19 if rowbegin<=rowend: 20 for i in range(colend,colbegin-1,-1): 21 res[rowend][i] = count 22 count += 1 23 rowend -= 1 24 if colbegin<=colend: 25 for i in range(rowend,rowbegin-1,-1): 26 res[i][colbegin] = count 27 count += 1 28 colbegin += 1 29 return res
62. Unique Paths 【Medium】 返回目录
题目:
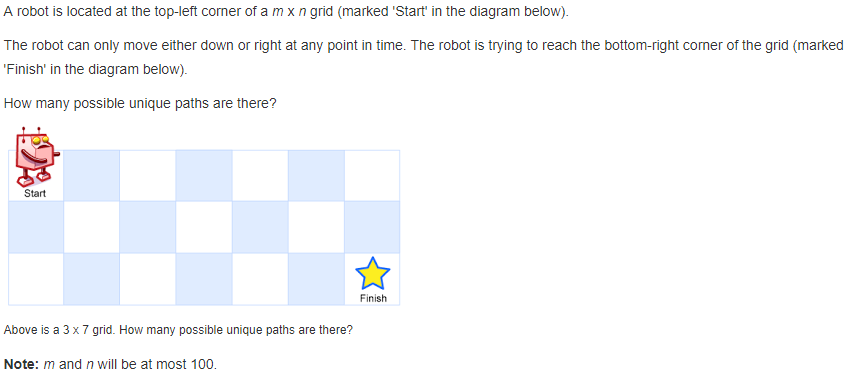
解题思路:
因为有很多子路是重复的,所以用动态规划比较好,最优子结构是 dp[i][j] = dp[i-1][j] + dp[i][j+1] 然后从目的地开始倒着填这张动态规划表就可以,倒着从行开始,再倒着列
code: 第一次写完代码一遍过,开心,决定再写一道
1 def uniquePaths(self, m, n): 2 """ 3 :type m: int 4 :type n: int 5 :rtype: int 6 """ 7 dp = [[1 for i in range(n)] for j in range(m)] 8 for i in range(m-2,-1,-1): 9 for j in range(n-2,-1,-1): 10 dp[i][j] = dp[i+1][j] + dp[i][j+1] 11 return dp[0][0]
对算法进行优化,时间复杂度变不了了O(mn), 看答案发现空间复杂度可以进行优化成O(min(m,n)), 可以只留下一行空间:
code:
1 def uniquePaths(self, m, n): 2 """ 3 :type m: int 4 :type n: int 5 :rtype: int 6 """ 7 if m > n: 8 return self.uniquePaths(n, m) 9 dp = [1 for i in range(m)] 10 for j in range(1,n): 11 for i in range(1,m): 12 dp[i] += dp[i-1] 13 return dp[m-1]
63. Unique Paths II 【Medium】 返回目录
题目:
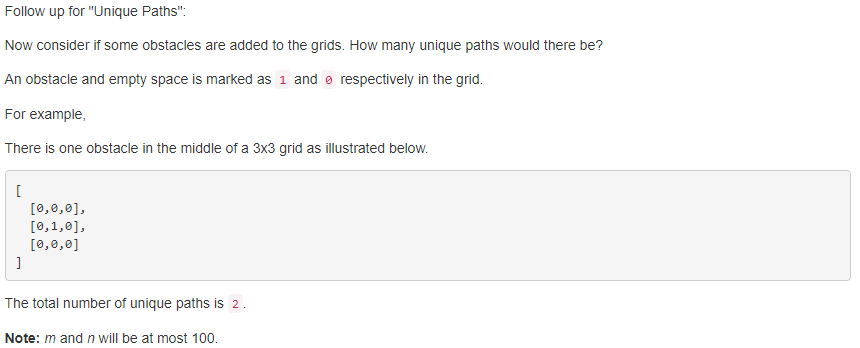
解题思路:
和上面一题一样,只不过多加了个障碍物,做法一样,倒着填dp表,只不过需要些限制条件,如果位置为1的话,那么计算的时候不能把它算在里面
首先要将0,1反过来,用0表示障碍物会方便计算
code:
1 def uniquePathsWithObstacles(self, obstacleGrid): 2 """ 3 :type obstacleGrid: List[List[int]] 4 :rtype: int 5 """ 6 m = len(obstacleGrid) 7 if not m: 8 return 0 9 n = len(obstacleGrid[0]) 10 if obstacleGrid[m-1][n-1] or obstacleGrid[0][0]: 11 return 0 12 dp = [[1-obstacleGrid[i][j] for j in range(n)] for i in range(m)] 13 for i in range(m-2,-1,-1): 14 dp[i][n-1] = dp[i+1][n-1] & dp[i][n-1] 15 for j in range(n-2,-1,-1): 16 dp[m-1][j] = dp[m-1][j+1] & dp[m-1][j] 17 for i in range(m-2,-1,-1): 18 for j in range(n-2,-1,-1): 19 print(i,j) 20 if dp[i][j]: 21 dp[i][j] = dp[i+1][j] + dp[i][j+1] 22 return dp[0][0]
64. Minimum Path Sum 【Medium】 返回目录
题目:


解题思路:
和前面两题一样,用动态规划做 dp[i][j] = min(dp[i+1][j],dp[i][j+1])+matrix[i][j]
code: 感觉现在自己做这种题都能一遍过呀,厉害厉害,鼓掌~
1 def minPathSum(self, grid): 2 """ 3 :type grid: List[List[int]] 4 :rtype: int 5 """ 6 m = len(grid) 7 if not m: 8 return 0 9 n = len(grid[0]) 10 for i in range(m-2,-1,-1): 11 grid[i][n-1] = grid[i][n-1] + grid[i+1][n-1] 12 for j in range(n-2,-1,-1): 13 grid[m-1][j] = grid[m-1][j] + grid[m-1][j+1] 14 for i in range(m-2,-1,-1): 15 for j in range(n-2,-1,-1): 16 grid[i][j] = min(grid[i+1][j],grid[i][j+1])+grid[i][j] 17 return grid[0][0]
73. Set Matrix Zeroes 【Medium】 返回目录
题目:


解题思路:
这道题看起来好像很容易,但是注意要求in place也就是不能用额外的空间,主要问题是当你处理遇到的第一个0的时候,你把当行当列都置为0,那么其他0的位置信息就被覆盖了,所以需要额外的空间存储之前0的位置信息,但是要求in place
所以就需要高效利用本身的空间,并且不冲掉已有信息,所以这里用每行的第一个位置记录每行的状态,每列的第一个位置记录每列的状态,因为row0 col0的位置重合了,所以需要额外的一个空间 O(1)算法
code: 这道题折腾了一下,想叉了,参考别人做法的
1 def setZeroes(self, matrix): 2 """ 3 :type matrix: List[List[int]] 4 :rtype: void Do not return anything, modify matrix in-place instead. 5 """ 6 m = len(matrix) 7 if not m: 8 return 9 n = len(matrix[0]) 10 col0 = 1 11 for i in range(m): 12 for j in range(n): 13 if not matrix[i][j]: 14 if not j: 15 col0 = 0 16 else: 17 matrix[0][j] = 0 18 matrix[i][0] = 0 19 for i in range(1,m): 20 for j in range(1,n): 21 if matrix[i][0]==0 or matrix[0][j]==0: 22 matrix[i][j] = 0 23 if not matrix[0][0]: 24 for j in range(1,n): 25 matrix[0][j] = 0 26 if not col0: 27 for i in range(m): 28 matrix[i][0] = 0
74. Search a 2D Matrix 【Medium】 返回目录
题目:
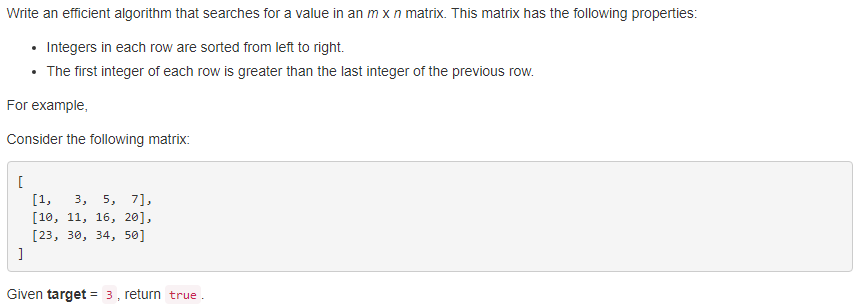
解题思路:
感觉这道题很简单,先按行使用二分法,确定target具体在哪一行,然后对于确定的行再用二分法,确定具体的列index
code:
1 def searchMatrix(self, matrix, target): 2 """ 3 :type matrix: List[List[int]] 4 :type target: int 5 :rtype: bool 6 """ 7 rowbegin = 0 8 rowend = len(matrix)-1 9 if rowend<0: 10 return False 11 colbegin = 0 12 colend = len(matrix[0])-1 13 if colend < 0: 14 return False 15 res = False 16 while rowbegin<=rowend: 17 midrow = (rowbegin+rowend)//2 18 if matrix[midrow][colbegin] <= target <= matrix[midrow][colend]: 19 while colbegin<=colend: 20 midcol = (colbegin+colend)//2 21 if matrix[midrow][midcol]==target: 22 res = True 23 return res 24 elif matrix[midrow][midcol]<target: 25 colbegin = midcol + 1 26 else: 27 colend = midcol - 1 28 return res 29 elif target > matrix[midrow][colend]: 30 rowbegin = midrow + 1 31 elif target < matrix[midrow][colbegin]: 32 rowend = midrow - 1 33 return res
code: 我的解法有点啰嗦,看了别人的解法,简洁才是美, 不要把它看成是一个二维数组,应该把它当做是一个一维数组直接使用二分法进行查找
1 def searchMatrix(self, matrix, target): 2 """ 3 :type matrix: List[List[int]] 4 :type target: int 5 :rtype: bool 6 """ 7 m = len(matrix) 8 if not m: 9 return False 10 n = len(matrix[0]) 11 l, r = 0, m*n-1 12 while l <= r: 13 mid = (l+r) // 2 14 if matrix[mid//n][mid%n] == target: 15 return True 16 elif matrix[mid//n][mid%n] < target: 17 l = mid + 1 18 else: 19 r = mid -1 20 return False
75. Sort Colors 【Medium】 返回目录
题目:


解题思路:
题目意思不是很好懂,就是说一个数组中有一堆0,1,2要你给排好序,相同数组排在一起,直接用nums.sort() 确实可以Accepted,但是因为是O(nlogn),所以时间很慢,提示要求只遍历一遍而且使用常数空间
我想的是用两个变量记录下1和2的开始的index,遇到相应的0,1就直接交换
code:
1 def sortColors(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: void Do not return anything, modify nums in-place instead. 5 """ 6 one = 0 7 two = 0 8 for i in range(len(nums)): 9 if nums[i] == 0: 10 if i>=one: 11 nums[i],nums[one] = nums[one],nums[i] 12 one += 1 13 if two < one: 14 two = one 15 if nums[i] == 1: 16 if i>=two: 17 nums[i],nums[two] = nums[two],nums[i] 18 two += 1
78. Subsets【Medium】 返回目录
题目:
解题思路:
递归求解,res做为参数传递
code:
1 def subsets(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: List[List[int]] 5 """ 6 res = [] 7 self.findset(res,0,[],nums) 8 return res 9 def findset(self,res,index,path,nums): 10 res.append(path) 11 for i in range(index,len(nums)): 12 self.findset(res,i+1,path+[nums[i]],nums) #这里注意不要把i+1写成了index+1导致报错
看了下其他的参考答案,觉得真的很精妙啊,有用位运算的,也有迭代算法,位运算是非常切合子集运算这个任务了
code: 位运算
1 def subsets(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: List[List[int]] 5 """ 6 res = [] 7 for i in range(1<<len(nums)): 8 tmp = [] 9 for j in range(len(nums)): 10 if i & 1<<j: #if i>>j & 1 看第j位是否为1,如果是就要加入到当前子集中 11 tmp.append(nums[j]) 12 res.append(tmp) 13 return res
code: 迭代算法
1 def subsets(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: List[List[int]] 5 """ 6 res = [[]] 7 for num in nums: 8 res += [item+[num] for item in res] 9 return res
79. Word Search【Medium】 返回目录
题目:

解题思路:
先通过二层循环找到第一个字符,然后再展开dfs,自己按死方法写了个代码,超时了,注意,每一个位置只能visit一次
code: 超时算法
1 def exist(self, board, word): 2 """ 3 :type board: List[List[str]] 4 :type word: str 5 :rtype: bool 6 """ 7 m = len(board) 8 if not m or not word: 9 return False 10 n = len(board[0]) 11 if not n: 12 return False 13 for i in range(m): 14 for j in range(n): 15 visit = [[0 for j in range(n)] for i in range(m)] 16 if board[i][j] == word[0]: 17 visit[i][j] = 1 18 if self.neiborfind(i,j,word,1,board,visit): 19 return True 20 return False 21 def neiborfind(self,i,j,word,index,board,visit): 22 if index==len(word): 23 return True 24 if i>0 and word[index]==board[i-1][j] and not visit[i-1][j]: 25 visit[i-1][j] = 1 26 if self.neiborfind(i-1,j,word,index+1,board,visit): 27 return True 28 visit[i-1][j] = 0 29 if j>0 and word[index]==board[i][j-1] and not visit[i][j-1]: 30 visit[i][j-1] = 1 31 if self.neiborfind(i,j-1,word,index+1,board,visit): 32 return True 33 visit[i][j-1] = 0 34 if i<len(board)-1 and word[index]==board[i+1][j] and not visit[i+1][j]: 35 visit[i+1][j] = 1 36 if self.neiborfind(i+1,j,word,index+1,board,visit): 37 return True 38 visit[i+1][j] = 0 39 if j<len(board[0])-1 and word[index]==board[i][j+1] and not visit[i][j+1]: 40 visit[i][j+1] = 1 41 if self.neiborfind(i,j+1,word,index+1,board,visit): 42 return True 43 visit[i][j+1] = 0 44 return False
code: Accepted 算法, 参考别人的, 发现原理和我自己写的几乎一样,就是写法高超了很多,膜拜膜拜
1 def exist(self, board, word): 2 if not board: 3 return False 4 for i in range(len(board)): 5 for j in range(len(board[0])): 6 if self.dfs(board, i, j, word): 7 return True 8 return False 9 10 def dfs(self, board, i, j, word): 11 if len(word) == 0: 12 return True 13 if i<0 or i>=len(board) or j<0 or j>=len(board[0]) or word[0]!=board[i][j]: 14 return False 15 tmp = board[i][j] 16 board[i][j] = "#" 17 res = self.dfs(board, i+1, j, word[1:]) or self.dfs(board, i-1, j, word[1:]) \ 18 or self.dfs(board, i, j+1, word[1:]) or self.dfs(board, i, j-1, word[1:]) 19 board[i][j] = tmp 20 return res
80. Remove Duplicates from Sorted Array II 【Medium】 返回目录
题目:

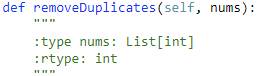
解题思路:
就简单遍历吧
code:
1 def removeDuplicates(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: int 5 """ 6 i = 0 7 while i < len(nums): 8 if i>0 and nums[i]==nums[i-1]: 9 j = i+1 10 while j<len(nums) and nums[j]==nums[i]: 11 nums.pop(j) 12 i += 1 13 return len(nums)
我的解法还是不够简洁,其实没有必要pop的,参考别人的算法(主要利用了题目的条件,数组是已经升序排列好的,并且It doesn't matter what you leave beyond the new length)
code:
1 def removeDuplicates(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: int 5 """ 6 i = 0 7 for num in nums: 8 if i<2 or num>nums[i-2]: 9 nums[i] = num #注意题目要求nums[:i+1]是剔除后的结果 10 i += 1 11 return i
81. Search in Rotated Sorted Array II 【Medium】 返回目录
题目:

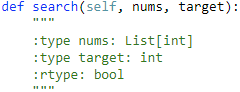
解题思路:
是 33 题中包含duplicates的情况,这样呢,就不方便事先判断mid是在左边还是在右边,如下面的情况

然后呢,就在判断左右边的情况下增加一种新的情况,就是当nums[mid] == nums[l], 那么就l++, 这样就可以转换成普通的情况了
比如上面,就转换成 [3,1,1,1]
code:
1 def search(self, nums, target): 2 """ 3 :type nums: List[int] 4 :type target: int 5 :rtype: bool 6 """ 7 l,r = 0,len(nums)-1 8 while l<=r: 9 mid = (l+r)//2 10 print(l,r,mid) 11 if nums[mid] == target: 12 return True 13 if nums[mid] > nums[l]: # left 14 if target>=nums[l] and target<nums[mid]: 15 r = mid -1 16 else: 17 l = mid + 1 18 elif nums[mid] < nums[l]: # right 19 if nums[mid]<target<=nums[r]: 20 l = mid + 1 21 else: 22 r = mid - 1 23 else: 24 l = l + 1 25 return False
90. Subsets II 【Medium】 返回目录
题目:
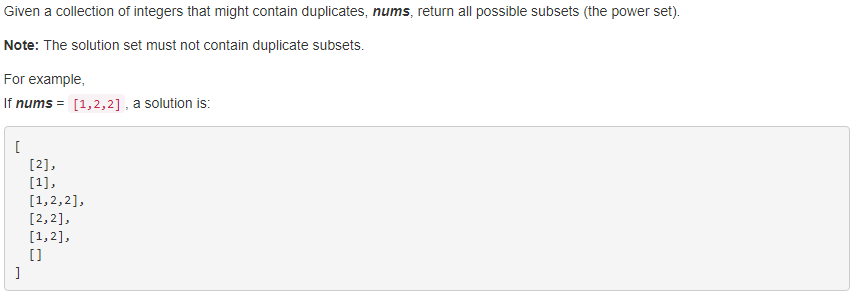

解题思路:
类似于78 subset, 但是在找到一个答案要加入到最终结果list时,进行判断是否已经存在
因为使用了if tmp not in res: res+=[tmp] 但是在list中[1,4]和[4,1]不是相同的,所以要事先进行排序,nums.sort()
code:
1 def subsetsWithDup(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: List[List[int]] 5 """ 6 nums.sort() 7 res = [[]] 8 for num in nums: 9 res += [n+[num] for n in res if n+[num] not in res] 10 return res
用位操作或者dfs也是相同地进行判断操作就行
105. Construct Binary Tree from Preorder and Inorder Traversal 【Medium】 返回目录
题目:


给前向遍历和中序遍历的序列,要求构建唯一的二叉树
解题思路:
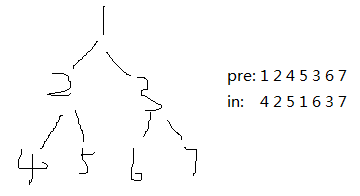
可以利用inorder找到对preorder的左右子树的划分
code: 参考答案的 解法真是精妙绝伦
1 # Definition for a binary tree node. 2 # class TreeNode: 3 # def __init__(self, x): 4 # self.val = x 5 # self.left = None 6 # self.right = None 7 8 class Solution: 9 def buildTree(self, preorder, inorder): 10 """ 11 :type preorder: List[int] 12 :type inorder: List[int] 13 :rtype: TreeNode 14 """ 15 if inorder: 16 ind = inorder.index(preorder.pop(0)) 17 root = TreeNode(inorder[ind]) 18 root.left = self.buildTree(preorder,inorder[0:ind]) 19 root.right = self.buildTree(preorder,inorder[ind+1:]) 20 return root
106. Construct Binary Tree from Inorder and Postorder Traversal 【Medium】 返回目录
题目:


解题思路:
同上面那题,只不过顺序是倒着的
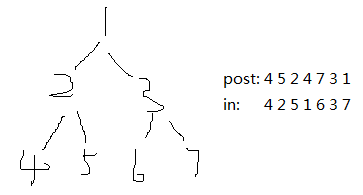
code:
1 # Definition for a binary tree node. 2 # class TreeNode: 3 # def __init__(self, x): 4 # self.val = x 5 # self.left = None 6 # self.right = None 7 8 class Solution: 9 def buildTree(self, inorder, postorder): 10 """ 11 :type inorder: List[int] 12 :type postorder: List[int] 13 :rtype: TreeNode 14 """ 15 if inorder: 16 ind = inorder.index(postorder.pop()) 17 root = TreeNode(inorder[ind]) 18 root.right = self.buildTree(inorder[ind+1:],postorder) 19 root.left = self.buildTree(inorder[0:ind],postorder) 20 return root
120. Triangle 【Medium】 返回目录
题目:
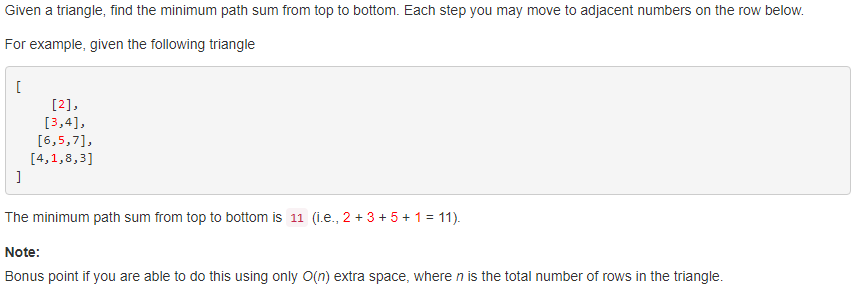
解题思路:
用了递归求解的方法,类似求二叉树的最大深度,进行左右子树的递归求解,但是在最后一个测试样例超时了,想了想发现很多路都是重复求解的,所以换成动态规划
code: 递归求解超时
1 def minimumTotal(self, triangle): 2 """ 3 :type triangle: List[List[int]] 4 :rtype: int 5 """ 6 return self.miniTree(triangle,0,0) 7 def miniTree(self,triangle,i,j): 8 if len(triangle)-1 == i: 9 return triangle[i][j] 10 return triangle[i][j] + min(self.miniTree(triangle,i+1,j),self.miniTree(triangle,i+1,j+1))
code: 动态规划
1 def minimumTotal(self, triangle): 2 """ 3 :type triangle: List[List[int]] 4 :rtype: int 5 """ 6 for i in range(len(triangle)-2,-1,-1): 7 for j in range(len(triangle[i])): 8 triangle[i][j] += min(triangle[i+1][j],triangle[i+1][j+1]) 9 return triangle[0][0]
152. Maximum Product Subarray 【Medium】 返回目录
题目:

解题思路:
用一个nxn数组 存dp[i][j]的结果 O(n^2)超时
这个时候就要看题目的特点了,进行简化运算
用一个变量来记录当前最好的结果,并不断比较更新,连乘到当前值的结果与当前值比较,如果还更小,直接断了连乘从当前位置重新开始
Tips:如果在一个数组中要求连续相乘或者相加的最大或最小值,那么当连续的结果还不如当前单个元素时,就要断了重新开始,对于有正负数的乘法时,只需要swap(max,min)
code: 参考答案
1 def maxProduct(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: int 5 """ 6 if not len(nums): 7 return 0 8 res = nums[0] 9 imax = imin = res 10 for i in range(1,len(nums)): 11 if nums[i] < 0: 12 imax,imin = imin,imax 13 imax = max(nums[i],imax*nums[i]) 14 imin = min(nums[i],imin*nums[i]) 15 16 res = max(res,imax) 17 return res 18
153. Find Minimum in Rotated Sorted Array【Medium】 返回目录
题目:

解题思路:
类似于 81. Search in Rotated Sorted Array II 进行二分搜索, 最小值要么在第一个位置,要么在右边的第一个
code:
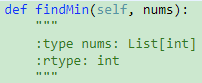
1 def findMin(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: int 5 """ 6 l,r = 0,len(nums)-1 7 if r<0: 8 return 9 imin = nums[0] 10 while l<=r: 11 mid = (l+r)//2 12 if nums[mid]<nums[mid-1]: 13 return min(imin,nums[mid]) 14 if nums[0] == nums[mid]: 15 l += 1 16 elif nums[0] < nums[mid]: #left 17 l = mid + 1 18 else: #right 19 r = mid - 1 20 return imin
看了下别人的解法,发现大神们往往都更加注重数据的特点,不会盲目地求解,都是高效利用数据的特点
code: 别人解法
1 def findMin(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: int 5 """ 6 l,r = 0,len(nums)-1 7 while l < r: 8 if nums[l] < nums[r]: 9 return nums[l] 10 mid = (l+r)//2 11 if nums[mid] >= nums[l]: 12 l = mid + 1 13 else: 14 r = mid 15 return nums[l]
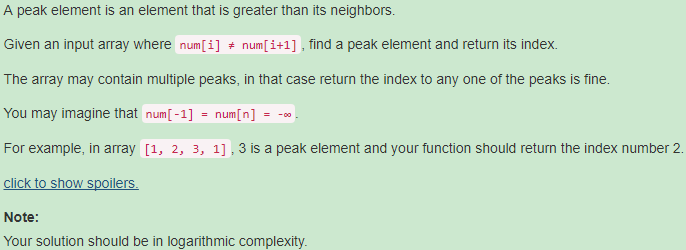
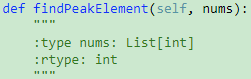
162. Find Peak Element【Medium】 返回目录
题目:
解题思路:要求O(logn),那么就是二分法了,直接二分法进行查询即可
code:
1 def findPeakElement(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: int 5 """ 6 l,r = 0,len(nums)-1 7 if not r: 8 return 0 9 while l <= r: 10 mid = (l+r)//2 11 if not mid and nums[mid]>nums[mid+1]: 12 return mid 13 if mid==len(nums) and nums[mid]>nums[mid-1]: 14 return mid 15 if 0<mid<len(nums)-1 and nums[mid-1]<nums[mid] and nums[mid]>nums[mid+1]: 16 return mid 17 elif mid>0 and nums[mid]>nums[mid-1]: 18 l = mid + 1 19 elif mid>0 and nums[mid]<nums[mid-1]: 20 r = mid - 1 21 else: 22 l = l + 1 23 return mid
一道这么简单的题都有好多种算法,算法真是美妙啊
参考别人的优美的解法
code: sequential search O(n)
1 def findPeakElement(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: int 5 """ 6 for i in range(1,len(nums)): 7 if nums[i]<nums[i-1]: 8 return i-1 9 return len(nums)-1
code: binary search
1 def findPeakElement(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: int 5 """ 6 l,r = 0,len(nums)-1 7 while l<r: 8 mid = (l+r)//2 9 if nums[mid]<nums[mid+1]: 10 l = mid + 1 11 else: 12 r = mid 13 return l
学到了,当l<r时,mid+1<=r的,所以一定取得到这个值,就不需要判断范围了,非常简约
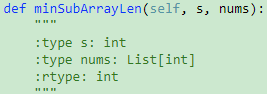
209. Minimum Size Subarray Sum【Medium】 返回目录
题目:

解题思路:我自己的想法之前就是数组所有元素加起来,然后不断减去两头比较小的数,但是有个问题就是当两头数字一样时就不确定要减去哪个,所以行不通
参考别人做法,O(n)算法就是使用两个指针,这样不断r++,l--就保持住了中间结果,只需要加减一个元素; O(nlogn)的做法就是先用O(n)算出个累加和的数组,然后又二分法进行查找
比如说:nums = [2, 3, 1, 2, 4, 3] sums = [0, 2, 5, 6, 8, 12, 15] 然后遍历数组作为i, r就在后面的数字中二分查找第一个>=sums[i]+s的数, 为什么要作累加和呢,因为这样就可以保证数组是升序的,可以很方便的利用二分法
code: O(N)
1 def minSubArrayLen(self, s, nums): 2 """ 3 :type s: int 4 :type nums: List[int] 5 :rtype: int 6 """ 7 res = 0 8 l,r = 0,-1 9 min_len = len(nums) 10 flag = False 11 while r<len(nums)-1: 12 r += 1 13 res += nums[r] 14 while res >= s: 15 flag = True 16 min_len = min(min_len, r-l+1) 17 res -= nums[l] 18 l += 1 19 return min_len if flag else 0
code: O(NlogN)
1 def minSubArrayLen(self, s, nums): 2 """ 3 :type s: int 4 :type nums: List[int] 5 :rtype: int 6 """ 7 sums = [0] 8 nums_len = len(nums) 9 for i in range(nums_len): 10 sums.append(nums[i]+sums[i]) 11 min_len = float('inf') 12 for i in range(nums_len): 13 j = self.binary_search(sums,i,nums_len+1,sums[i]+s) 14 if j==-1: 15 break 16 min_len = min(min_len,j-i) 17 return min_len if min_len!=float('inf') else 0 18 def binary_search(self,nums,i,nums_len,target): 19 l,r = i,nums_len-1 20 while l<r: 21 mid = (l+r)//2 22 if nums[mid]>=target: 23 r = mid 24 else: 25 l = mid + 1 26 return l if nums[l]>=target else -1
216. Combination Sum III【Medium】 返回目录
题目:
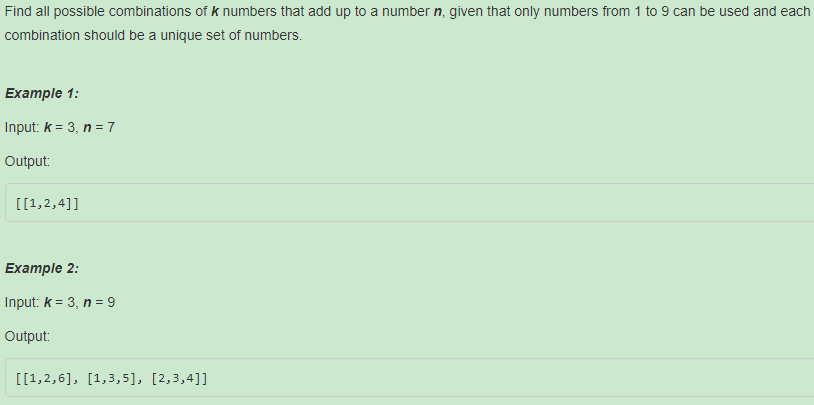

解题思路:和之前的 39. Combination Sum 一个套路
code:
1 def combinationSum3(self, k, n): 2 """ 3 :type k: int 4 :type n: int 5 :rtype: List[List[int]] 6 """ 7 nums = [1,2,3,4,5,6,7,8,9] 8 res = [] 9 self.find(res,nums,0,k,[],n) 10 return res 11 def find(self,res,nums,index,k,path,remains): 12 if len(path)==k and not remains: 13 res.append(path) 14 return 15 if len(path)==k: 16 return 17 for i in range(index,len(nums)): 18 self.find(res,nums,i+1,k,path+[nums[i]],remains-nums[i]) 19
228. Summary Ranges【Medium】 返回目录
题目:

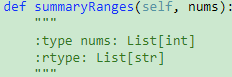
解题思路:直接从左到右遍历一遍 O(N)
code:
1 def summaryRanges(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: List[str] 5 """ 6 res = [] 7 i = 0 8 while i<len(nums)-1: 9 temp = str(nums[i]) 10 while i<len(nums)-1 and nums[i+1] == nums[i]+1: 11 i += 1 12 if i>0 and nums[i]==nums[i-1]+1: 13 temp = temp + "->" + str(nums[i]) 14 res.append(temp) 15 i += 1 16 if i==len(nums)-1: 17 res.append(str(nums[-1])) 18 return res
229. Majority Element II【Medium】 返回目录
题目:

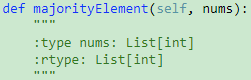
解题思路:
自己完全没想法,看了参考答案,发现了一个叫做 Boyer-Moore Majority Vote algorithm(摩尔投票算法),可以解决求无序数列中多于n/2, n/3....的元素。
对于大于一半的数很简单,就是用两个变量,一个candidate记录可能是结果的元素,一个count记录当前的个数,当count为0时,candidate就设置为当前数字,如果当前数字和candidate一样,count++, 如果不同,count--,就相当于一直在找不一样的一对数字,找到了就消去这两个数字(类似于连连看),那么最后剩下的数字就是最终结果了,对于大于n/3的元素,就需要设置两个candidate,算法同上,只不过最后判断是否是真的结果时,还需要遍历一遍进行确认。
code: 参考
1 def majorityElement(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: List[int] 5 """ 6 count1 = count2 = 0 7 candidate1 = candidate2 = None 8 for i in range(len(nums)): 9 if nums[i] == candidate1: 10 count1 += 1 11 elif nums[i] == candidate2: 12 count2 += 1 13 elif not count1: 14 candidate1 = nums[i] 15 count1 += 1 16 elif not count2: 17 candidate2 = nums[i] 18 count2 += 1 19 else: 20 count1 -= 1 21 count2 -= 1 22 res = [] 23 if nums.count(candidate1) > len(nums)//3: 24 res.append(candidate1) 25 if nums.count(candidate2) > len(nums)//3: 26 res.append(candidate2) 27 return res
感觉自己写代码还是不够简洁,虽然思想一样,但是大神的代码看起来就是简洁有美感
1 def majorityElement(self, nums): 2 if not nums: 3 return [] 4 count1, count2, candidate1, candidate2 = 0, 0, 0, 1 5 for n in nums: 6 if n == candidate1: 7 count1 += 1 8 elif n == candidate2: 9 count2 += 1 10 elif count1 == 0: 11 candidate1, count1 = n, 1 12 elif count2 == 0: 13 candidate2, count2 = n, 1 14 else: 15 count1, count2 = count1 - 1, count2 - 1 16 return [n for n in (candidate1, candidate2) 17 if nums.count(n) > len(nums) // 3]
238. Product of Array Except Self【Medium】 返回目录
题目:


解题思路:
不让用除法,那么就用乘法,用两个数组left_mul和right_mul分别记录从左到右和从右到左累乘的结果,然后res[i]=left[i-1]*right[i+1]
这样的话花费时间 O(n) 花费空间也是O(n)
额外的奖励就是希望能用O(1)的空间解决
code: O(n) time O(n) space
1 def productExceptSelf(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: List[int] 5 """ 6 left_mul = [1] 7 for num in nums: 8 left_mul.append(num*left_mul[-1]) 9 right_mul = [ 1 for i in range(len(nums)+1)] 10 for i in range(len(nums)-1,-1,-1): 11 right_mul[i] = nums[i]*right_mul[i+1] 12 res = [] 13 for i in range(len(nums)): 14 res.append(left_mul[i]*right_mul[i+1]) 15 return res
我这个思路是正确的,怎么将上面的代码修改成O(1) space呢(不包括res占的空间),那么就只能用res数组表示left_mul,然后right数组用一个right变量表示就行
code: 参考别人的
1 def productExceptSelf(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: List[int] 5 """ 6 res = [1] 7 for i in range(1,len(nums)): 8 res.append(res[i-1]*nums[i-1]) 9 right = 1 10 for i in range(len(nums)-1,-1,-1): 11 res[i] *= right 12 right *= nums[i] 13 return res
287. Find the Duplicate Number 【Medium】 返回目录
题目:

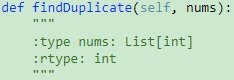
解题思路:
不能修改原数组且只能用O(1) space,也就是说不能对原数组进行排序,参考别人的解法,发现用链表进行判断环路的方法可以用O(n)的方法实现
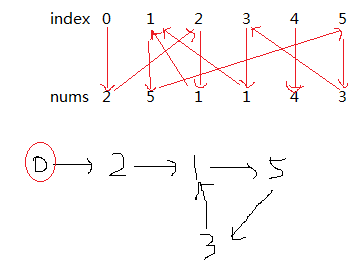
有两个箭头指向1,说明有环路了,而重复的数字呢就是这个环路的入口元素,首先要找到这个环路,然后再找到入口元素。
找环路过程用两个指针,一个fast,一个slow,fast一次走两步,slow一次走一步,它们两个总是会在环路内部相遇的
设环路前面的一段路长k,当slow走到入口处时,fast已经走到环路上的k处,假设它们再走c次相遇,那么c = n-k,也就是说他们的相遇点在slow走上环路后的c位置
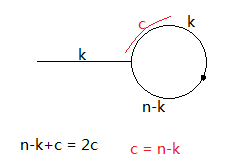
那么求入口位置就可以很好计算了,因为c = n-k, 那么用一个A指针从头开始走起,然后从相遇的地方B指针走起,两个指针都是一次走一步,那么相遇的地方就是入口处,因为两个指针都走k步就相同了
code: O(n) 判断链表中的环路
1 def findDuplicate(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: int 5 """ 6 if not len(nums): 7 return 8 slow,fast = nums[0],nums[nums[0]] 9 while slow!= fast: 10 slow = nums[slow] 11 fast = nums[nums[fast]] 12 fast = 0 13 while fast!=slow: 14 fast = nums[fast] 15 slow = nums[slow] 16 return slow
还看到有一种二分的解法O(nlogn)就是对[1,n]二分查找,对mid,统计小于mid的个数O(n),如果count[mid]>mid,说明在[1,mid]部分有重复的元素,否则就在[mid:]里面
总的时间复杂度就是O(nlogn)
code: O(nlogn)
1 def findDuplicate(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: int 5 """ 6 if not len(nums): 7 return 8 l,r = 1,len(nums)-1 9 while l<r: 10 mid = (l+r)//2 11 count = 0 12 for num in nums: 13 if num<= mid: 14 count += 1 15 if count>mid: 16 r = mid 17 else: 18 l = mid+1 19 return l
注意一个问题,我经常把r=mid 写成r=mid-1 当nums<=mid情况下左边是包含mid的,注意是否要考虑mid的情况
289. Game of Life 【Medium】 返回目录
题目:


解题思路:
要求in-place所以不能有额外的空间,所有信息都必须存在当前board上,但是又不能冲刷掉前面的信息,想不到怎么弄,看参考答案
说是用2bit数[0-3]来代表第一个bit表示下个状态,第二个bit表示当前状态,这样既可以存当前信息也可以存历史信息,bravo!!!!!!
比如说 00 当前状态dead 下一个状态dead 01 当前状态live 下个状态dead
而且还有个好处就是这样设置就可以很方便地使用位操作 取当前状态 board[i][j] & 1 取下一个状态 board[i][j] >> 1
code: O(mn) time O(1) space
1 def gameOfLife(self, board): 2 """ 3 :type board: List[List[int]] 4 :rtype: void Do not return anything, modify board in-place instead. 5 """ 6 m = len(board) 7 if not m: 8 return 9 n = len(board[0]) 10 for i in range(m): 11 for j in range(n): 12 live = self.neibor(board,m,n,i,j) 13 if board[i][j] == 1 and live>=2 and live<=3: #current alive 14 board[i][j] = 3 15 elif not board[i][j] and live==3: #current dead 16 board[i][j] = 2 17 for i in range(m): 18 for j in range(n): 19 board[i][j] >>= 1 20 def neibor(self,board,m,n,i,j): 21 live = 0 - (board[i][j] & 1) 22 for p in range(max(i-1,0),min(i+2,m)): 23 for q in range(max(j-1,0),min(j+2,n)): 24 live += board[p][q] & 1 25 return live
注意: 0 - 1 & 1结果是1 要加上括号才是正确结果-1 +/-的优先级比 &高 比&&低
最后一段关于边界判断的看别人写法是在太妙,自己写都是额外的if判断
380. Insert Delete GetRandom O(1) 【Medium】 返回目录
题目:
解题思路:
O(1)时间复杂度,不就是hash表吗,在python中体现为dict字典,可是对于字典它remove的时候不太好操作,因为要遍历index,所以这里就需要用列表存数据,用dict存index
1 import random 2 class RandomizedSet: 3 4 def __init__(self): 5 """ 6 Initialize your data structure here. 7 """ 8 self.nums = [] 9 self.length = 0 10 self.index = {} 11 12 13 def insert(self, val): 14 """ 15 Inserts a value to the set. Returns true if the set did not already contain the specified element. 16 :type val: int 17 :rtype: bool 18 """ 19 if val not in self.index: 20 self.nums.append(val) 21 self.length += 1 22 self.index[val] = self.length - 1 23 return True 24 return False 25 26 27 def remove(self, val): 28 """ 29 Removes a value from the set. Returns true if the set contained the specified element. 30 :type val: int 31 :rtype: bool 32 """ 33 if val in self.index: 34 ind,last = self.index[val],self.nums[-1] 35 self.nums[ind],self.index[last] = last,ind 36 self.nums.pop() 37 self.index.pop(val) 38 self.length -= 1 39 return True 40 return False 41 42 43 def getRandom(self): 44 """ 45 Get a random element from the set. 46 :rtype: int 47 """ 48 return self.nums[random.randint(0, self.length-1)] 49 50 51 # Your RandomizedSet object will be instantiated and called as such: 52 # obj = RandomizedSet() 53 # param_1 = obj.insert(val) 54 # param_2 = obj.remove(val) 55 # param_3 = obj.getRandom()
442. Find All Duplicates in an Array【Medium】 返回目录
题目:

解题思路:
O(n)时间 不许有额外空间 好难啊,想不出,看参考答案,真是精妙啊,感觉每天都要被各种设计巧妙的算法惊艳
如果不能使用额外的空间,那么就需要在当前已有的数组上看能否存上额外的信息,比如289. Game of Life 本身是0/1扩展成多位数据,用多出来的位数存储额外信息
这里使用当前元素的正负号作为额外的信息保存到当前数组,对数字i 用i-1(减一是因为1~n换成index从0开始)位置上元素负号表示已经出现过一次了,这样遍历完成后,所有负数对应index+1就是duplicates
code: O(n) beat 100% 第一次100% 虽然是参考的答案,但是还是很感动啊,算法真的是很美妙,我爱算法!!
1 def findDuplicates(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: List[int] 5 """ 6 res = [] 7 for num in nums: 8 num = abs(num) 9 if nums[num-1]<0: 10 res.append(num) 11 else: 12 nums[num-1] = -nums[num-1] 13 return res
还看到了另外一种算法也是beat100% 666~

将数组中的值与index对应,对应不上的多余值 [2,3]就是duplicates
code:
1 def findDuplicates(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: List[int] 5 """ 6 i = 0 7 res = [] 8 while i < len(nums): 9 if nums[i]!=nums[nums[i]-1]: 10 temp = nums[nums[i]-1] 11 nums[nums[i]-1] = nums[i] 12 nums[i] = temp 13 #nums[i],nums[nums[i]-1] = nums[nums[i]-1],nums[i] wrong because nums[nums[i]-1]中也用到了nums[i] 14 else: 15 i += 1 16 for i in range(len(nums)): 17 if nums[i]!=i+1: 18 res.append(nums[i]) 19 return res
从头遍历循环,对于i直到找到与它相同的元素否则不断交换,每一次交换都一定确定了一个位置的正确对应,然后再移到下一个位置
495. Teemo Attacking【Medium】 返回目录
题目:


解题思路:
这道题很简单,就是一个数轴覆盖长度问题,用一个end变量记录下当前覆盖到的最大长度,然后再进行覆盖的时候和它比较一下
code: beat 2.5%
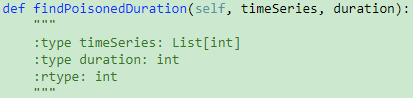
1 def findPoisonedDuration(self, timeSeries, duration): 2 """ 3 :type timeSeries: List[int] 4 :type duration: int 5 :rtype: int 6 """ 7 res = 0 8 end = 0 9 for i in range(len(timeSeries)): 10 if timeSeries[i]+duration > end: 11 res += min(timeSeries[i]+duration-end,duration) 12 end = max(end,timeSeries[i]+duration) 13 return res
别人的解法: beat 25%
1 def findPoisonedDuration(self, timeSeries, duration): 2 ans = duration * len(timeSeries) 3 for i in range(1,len(timeSeries)): 4 ans -= max(0, duration - (timeSeries[i] - timeSeries[i-1])) 5 return ans
560. Subarray Sum Equals K【Medium】 返回目录
题目:
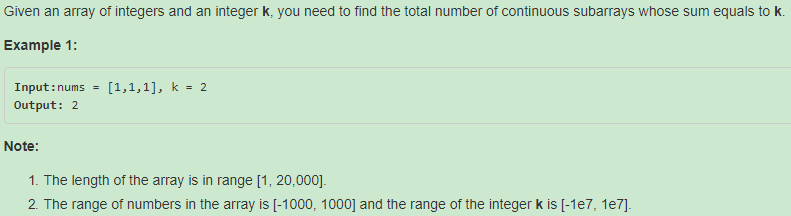
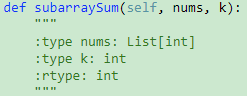
解题思路:
这道题指明是整数,没有说是正整数,所以用变量保存当前和,然后减去头加上尾的方式不可行,那么首先先想暴力方法O(n) sum(i,j)
想要进行优化,那么就事先求出presum sum(i,j)=sum(j)-sum(i)
在遍历过程中同时寻找满足sum(j)-sum(i)==k 的i
code: O(n) time O(n) space
1 def subarraySum(self, nums, k): 2 """ 3 :type nums: List[int] 4 :type k: int 5 :rtype: int 6 """ 7 accu_sum = {0:1} 8 res = s = 0 9 for num in nums: 10 s += num 11 res += accu_sum.get(s-k,0) 12 accu_sum[s] = accu_sum.get(s,0)+1 13 return res
565. Array Nesting【Medium】 返回目录
题目:

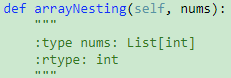
解题思路:
暴力搜索呗,$O(n^2)$ 超时了
1 def arrayNesting(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: int 5 """ 6 res = 0 7 for i in range(len(nums)): 8 count = 0 9 k = i 10 while(nums[k]>0 and nums[k]!=i): 11 k = nums[k] 12 count += 1 13 res = max(res,count+1) 14 return res
想想改进的方法:想不出,参考别人答案 O(n)
1 def arrayNesting(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: int 5 """ 6 res = 0 7 for i in range(len(nums)): 8 count = 0 9 k = i 10 while(nums[k]>0 and nums[k]!=i): 11 temp = k 12 k = nums[k] 13 nums[temp] = -1 14 count += 1 15 res = max(res,count+1) 16 return res
其实不同之处就是多加了两句话,当遍历过一遍后就标记之后不再遍历,原因是如下,其实这是形成了多个环,当你第一步踏进一个环时,长度就是该环的长度,所以说看第一步踏进了与之前不同的环,得出的结果才可能不同
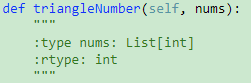
611. Valid Triangle Number【Medium】 返回目录
题目:
解题思路:
先确定两条边,然后确定另外一条边,确定两条边的时候$O(n^2)$,所以先排序确定第三条边的时候用遍历超时了
code: O(TLE) $O(n^3)$
1 def triangleNumber(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: int 5 """ 6 nums.sort() 7 res = 0 8 for i in range(len(nums)): 9 for j in range(i+1,len(nums)): 10 l = abs(nums[i]-nums[j]) 11 r = nums[i]+nums[j] 12 for k in range(j+1,len(nums)): 13 if nums[k]>=r: 14 break 15 elif nums[k]<=l: 16 continue 17 else: 18 res += 1 19 return res
参考别人答案,发现,审题很重要,发现题目的一些特殊性质很重要,比如说能构成三角形的条件,我之前设置的条件就太复杂了,其实只要满足两小边之和大于最大边就行了
因为,已知 a,b < c 如果a+b>c => a>c-b && b>c-a
而且如果按升序排好,倒着来取最大边c,那么只需要对当前index前面取两个数满足 a+b>c即可,同时a,b的取法也是由[0,index-1]两端取法,这样的话当0,index-1满足条件,那么0~index-1中间的数都可作为a满足,因为是逐渐变大的,所以这时的取值可能情况是index-1-0+1,同时b的下标减一,求另外的解法;若这时取值a+b<=c,只需要移动a的下标加一让数字变大即可
1 def triangleNumber(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: int 5 """ 6 nums.sort() 7 res = 0 8 for i in range(len(nums)-1,1,-1): 9 l,r = 0,i-1 10 while l<r: 11 if nums[l]+nums[r]>nums[i]: 12 res += r-l 13 r -= 1 14 else: 15 l += 1 16 return res
621. Task Scheduler【Medium】 返回目录
题目:

解题思路:
这题因为所有任务都是等间距的,所以想用贪心法做,先对所有任务的耗时进行反向排序,用一个长度为n的数组记录下可填充的每列的end位置,当要填充一个任务时,就看min(end)进行填充就好了
代码如下,错了,可以通过58个测试,剩下的测试过不了
1 def leastInterval(self, tasks, n): 2 """ 3 :type tasks: List[str] 4 :type n: int 5 :rtype: int 6 """ 7 if not n: 8 return len(tasks) 9 count = {} 10 for t in tasks: 11 count[t] = count.get(t,0)+1 12 nums = sorted(count.values(),reverse=True) 13 end = [-i for i in range(n+1,0,-1)] 14 for i in nums: 15 ind = end.index(min(end)) 16 end[ind] += i*(n+1) 17 return max(end)+1
参考别人的解法,发现这种贪心算法是有问题的,可以不连续,反而是间隔着插入

主要是找到这个排列的规律

正确的code如下:
1 def leastInterval(self, tasks, n): 2 """ 3 :type tasks: List[str] 4 :type n: int 5 :rtype: int 6 """ 7 task_counts = list(collections.Counter(tasks).values()) 8 M = max(task_counts) 9 Mct = task_counts.count(M) 10 return max(len(tasks), (M - 1) * (n + 1) + Mct)
667. Beautiful Arrangement II【Medium】 返回目录
题目:

Example1:
Input: n = 3, k = 1 Output: [1, 2, 3] Explanation: The [1, 2, 3] has three different positive integers ranging from 1 to 3, and the [1, 1] has exactly 1 distinct integer: 1.
Example2:
Input: n = 3, k = 2 Output: [1, 3, 2] Explanation: The [1, 3, 2] has three different positive integers ranging from 1 to 3, and the [2, 1] has exactly 2 distinct integers: 1 and 2.

解题思路:
如果有k种间距的话,那么就是k,k-1,k-2,....1 所以将 1,k+1, 2, k, 3, k-1,....... 就有间距 k,k-1,k-2,k-3,k-4,以此类推
code: 完全自己想的,一遍过,好开心
1 def constructArray(self, n, k): 2 """ 3 :type n: int 4 :type k: int 5 :rtype: List[int] 6 """ 7 res = [i+1 for i in range(n)] 8 j = 1 9 for i in range(0,k+1,2): 10 res[i] = j 11 j += 1 12 j = k+1 13 for i in range(1,k+1,2): 14 res[i] = j 15 j -= 1 16 return res
670. Maximum Swap【Medium】 返回目录
题目:
给一个非负整数,只能交换两个数位上的数组,给出交换后可能的结果中的最大值
解题思路:
想着说先倒序排序,然后对比原数和倒序排序后数,第一个遇到的不一样的数字进行交换,结果发现当有相同数字时,不知道该交换哪个,还是思考得不够周全
code: wrong
1 def maximumSwap(self, num): 2 """ 3 :type num: int 4 :rtype: int 5 """ 6 num_str = list(str(num)) 7 num_max = sorted(num_str,reverse=True) 8 i = 0 9 while(i<len(num_str) and num_str[i]==num_max[i]): 10 i += 1 11 if i != len(num_str): 12 ind = i+num_str[i:].index(num_max[i]) 13 num_str[i],num_str[ind] = num_str[ind],num_str[i] 14 return int("".join(num_str))
code: 考虑上述情况的修改后AC代码 O(NlogN)
1 def maximumSwap(self, num): 2 """ 3 :type num: int 4 :rtype: int 5 """ 6 num_str = list(str(num)) 7 num_max = sorted(num_str,reverse=True) 8 i = 0 9 while(i<len(num_str) and num_str[i]==num_max[i]): 10 i += 1 11 res = num 12 if i != len(num_str): 13 candidates = [k for (k,v) in enumerate(num_str[i:]) if v==num_max[i]] 14 for j in candidates: 15 num_str[i],num_str[i+j] = num_str[i+j],num_str[i] 16 res = max(res,int("".join(num_str))) 17 num_str[i],num_str[i+j] = num_str[i+j],num_str[i] 18 return res
上述算法因为要排序,所以是O(nlogn)算法
在本题中数据长度最多为8,所以无所谓,若是没有这个限制呢,所以还是需要更优的解法
看了下别人的解法,和我真的是相同的想法,但是实现得很精妙,而且比我想得更加透彻,首先因为n比较小所以不要用O(nlogn)进行排序,反而是用O(n)记录下每个数字出现的最后一次的index,交换从大到小的数字,只要遇到不相等的,就用最后的那个数交换,这里就是比我精妙的地方,我是顺序遍历,人家倒序遍历找交换的位置,机智,这样就不用再比较结果了
1 def maximumSwap(self, num): 2 """ 3 :type num: int 4 :rtype: int 5 """ 6 num_str = list(str(num)) 7 last_index = {} 8 for i in range(len(num_str)): 9 last_index[num_str[i]] = i 10 for i in range(len(num_str)): 11 for k in range(9,0,-1): 12 ind = last_index.get(str(k),None) 13 if ind and ind>i and num_str[ind]>num_str[i]: 14 num_str[ind],num_str[i] = num_str[i],num_str[ind] 15 return int("".join(num_str)) 16 return num
713. Subarray Product Less Than K【Medium】 返回目录
题目:

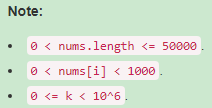
Example1:
Input: nums = [10, 5, 2, 6], k = 100 Output: 8 Explanation: The 8 subarrays that have product less than 100 are: [10], [5], [2], [6], [10, 5], [5, 2], [2, 6], [5, 2, 6]. Note that [10, 5, 2] is not included as the product of 100 is not strictly less than k.
解题思路:
因为全部都是正整数,所以可以用temp记录下当前index连乘后的结果,然后除去nums[index]作为index+1的起始结果,这样的话可以简化很多计算,注意想问题时,一定要想清楚变量具体代表的什么含义,才能对初始值或者计算式进行良好地定义。
code:错了,只通过了78/84个测试样例,说明考虑得还不够全面,漏掉了一些特殊情况
1 def numSubarrayProductLessThanK(self, nums, k): 2 """ 3 :type nums: List[int] 4 :type k: int 5 :rtype: int 6 """ 7 if not k: 8 return 0 9 nums.append(1) 10 res = 0 11 temp = 1 12 j = 0 13 for i in range(len(nums)-1): 14 temp = temp//nums[i-1] 15 res += max(j-i,0) 16 temp = temp * nums[j] 17 while temp<k: 18 res += 1 19 j = j+1 20 if j<len(nums)-1: 21 temp = temp*nums[j] 22 else: 23 return res+(j-1-i)*(j-i)//2 24 temp = temp // nums[j] 25 return res
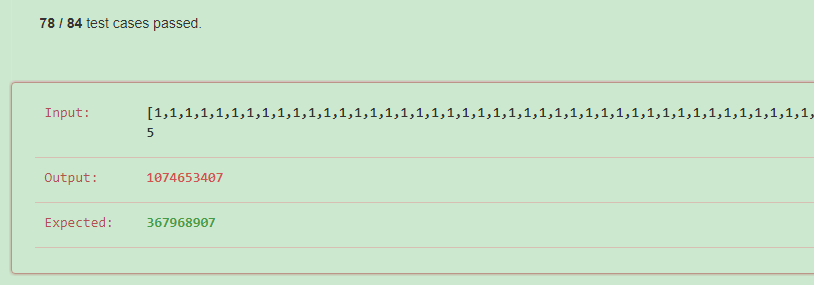
看了下参考答案,思路都是差不多,就是实现方法更全面,而且考虑的情况更加全面,我真的应该学习下写代码的自我修养
code: 参考别人
1 def numSubarrayProductLessThanK(self, nums, k): 2 """ 3 :type nums: List[int] 4 :type k: int 5 :rtype: int 6 """ 7 if k<= 1: 8 return 0 9 res = 0 10 temp = 1 11 j = 0 12 for i in range(len(nums)): 13 if i>0 and i<=j: 14 temp = temp//nums[i-1] 15 else: 16 j = i 17 while j<len(nums) and temp*nums[j]<k: 18 temp = temp*nums[j] 19 j += 1 20 res += j-i 21 return res
对比这两份代码
主要是没有开头的if-else的判断j代表的是正好<k的下标加一;temp是正好<k的连乘
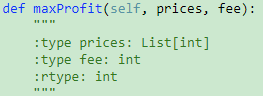
714. Best Time to Buy and Sell Stock with Transaction Fee【Medium】 返回目录
题目:

解题思路:
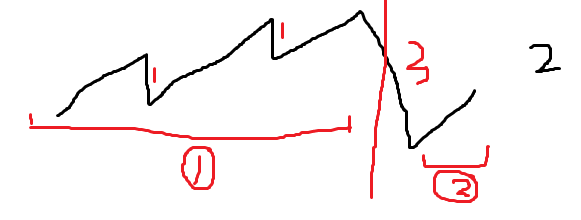
从开头开始找上坡,如果上坡减去fee>0(第一个坡) 如果可连续,对于续上的坡,只需要坡>之前下降的部分就可以直接续上,而且不用再交费用了,如果续不上直接断掉
提交了一个版本的代码发现只能通过26/44个测试样例
code: wrong 26/44
1 def maxProfit(self, prices, fee): 2 """ 3 :type prices: List[int] 4 :type fee: int 5 :rtype: int 6 """ 7 i = 1 8 res = 0 9 concat = False 10 remain = 0 11 while i<len(prices): 12 start = prices[i-1] 13 while(i<len(prices) and prices[i]>=prices[i-1]): 14 i += 1 15 if concat: 16 if prices[i-1]-start>=remain: 17 res += prices[i-1]-start-remain 18 else: 19 concat = False 20 remain = 0 21 else: 22 if prices[i-1]-start>=fee: 23 res += prices[i-1]-start-fee 24 concat = True 25 start = prices[i-1] 26 while(i<len(prices) and prices[i]<=prices[i-1]): 27 i += 1 28 if start-prices[i-1]>fee: 29 concat = False 30 else: 31 concat = concat and True 32 if concat: 33 remain = start-prices[i-1] 34 return res
但是发现这个代码有种情况没考虑到,就是前面短后面长的情况考虑不到,所以还是应该把它转换成连续子数组和的方式

修改了一个版本,还是有问题,想不明白自己家还少考虑了哪一部分
code: 22/44 pass
1 def maxProfit(self, prices, fee): 2 """ 3 :type prices: List[int] 4 :type fee: int 5 :rtype: int 6 """ 7 if len(prices)<= 1: 8 return 0 9 earn = [] 10 res = 0 11 i = 0 12 flag = False 13 while i < len(prices)-1: 14 start = prices[i] 15 while i<len(prices)-1 and prices[i+1]>=prices[i]: 16 i += 1 17 flag = True 18 if flag: 19 earn.append(prices[i]-start) 20 if i <len(prices)-1: 21 start = prices[i] 22 while i<len(prices)-1 and prices[i+1]<=prices[i]: 23 i += 1 24 earn.append(prices[i]-start) 25 26 concat = False 27 28 print(earn,len(earn)) 29 30 i = 0 31 remain = 0 32 while i < len(earn)-2: 33 # import pdb 34 # pdb.set_trace() 35 if not concat: 36 while i < len(earn)-2 and earn[i]<=0: 37 i += 1 38 if earn[i]>=fee: 39 res += earn[i]-fee 40 concat = True 41 elif earn[i]+earn[i+1]>0: 42 remain = earn[i]+earn[i+1] 43 concat = True 44 i += 2 45 else: 46 i += 2 47 else: 48 if remain>0: 49 if remain + earn[i] > fee: 50 res += remain + earn[i] - fee 51 remain = 0 52 elif earn[i]+earn[i+1]>0: 53 remain += earn[i]+earn[i+1] 54 i += 2 55 else: 56 concat = False 57 i += 2 58 remain = 0 59 else: 60 if abs(earn[i+1])<=min(earn[i+2],fee): 61 res += earn[i+1]+earn[i+2] 62 i += 2 63 else: 64 concat = False 65 i = i+2 66 if not concat and earn[i]>fee: 67 res += earn[i]-fee 68 return res
开始做题前没完全考虑清楚所有的可能性,经常就是写完code后只能通过部分测试样例,下笔前请好好思考清楚
参考答案,真的太厉害了
用s0表示当前手上没有股票利润
用s1表示当前手上有一只股票时的利润
code:
1 def maxProfit(self, prices, fee): 2 """ 3 :type prices: List[int] 4 :type fee: int 5 :rtype: int 6 """ 7 s0 = 0 8 s1 = -float('inf') 9 for p in prices: 10 tmp = s0 11 s0 = max(s0,s1+p) 12 s1 = max(s1,tmp-p-fee) 13 return s0
代码中先是-p1, 然后是+p2 其实就是求一个p2-p1过一天赚的利润,只是通过这种方式的话就只需要O(1) space 不需要额外的空间保存每天的利润,真是太巧妙了
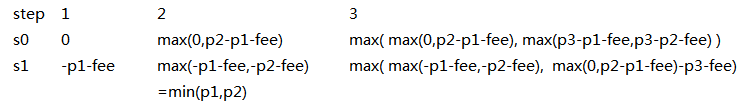
太精妙了,我要给这道题打三颗星
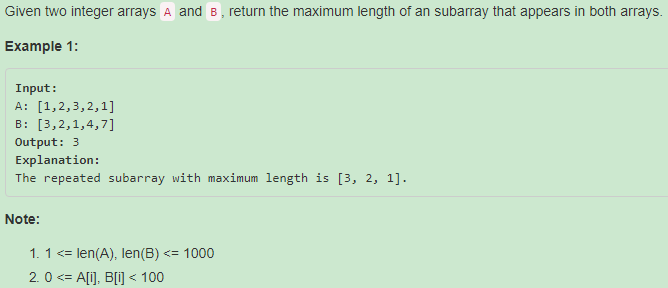
718. Maximum Length of Repeated Subarray【Medium】 返回目录
题目:
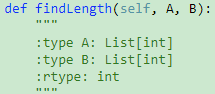
解题思路:
固定A,每次将B往后滑动一个index与A对齐,计算最大res,然后交换A,B的位置再求一次 ,取最大的结果,居然一遍AC了,感动,但是耗时有点多$O(n^2)$
code:
1 def findLength(self, A, B): 2 """ 3 :type A: List[int] 4 :type B: List[int] 5 :rtype: int 6 """ 7 res = 0 8 for i in range(len(A)): 9 res = max(res,self.compare(A,i,B)) 10 for i in range(len(B)): 11 res = max(res,self.compare(B,i,A)) 12 return res 13 def compare(self,A,k,B): 14 i,j = k,0 15 res = 0 16 while i<len(A): 17 while i<len(A) and A[i]!=B[j]: 18 i += 1 19 j += 1 20 temp = i 21 while i<len(A) and A[i]==B[j]: 22 i += 1 23 j += 1 24 res = max(res,i-temp) 25 return res
729. My Calendar I【Medium】 返回目录
题目:

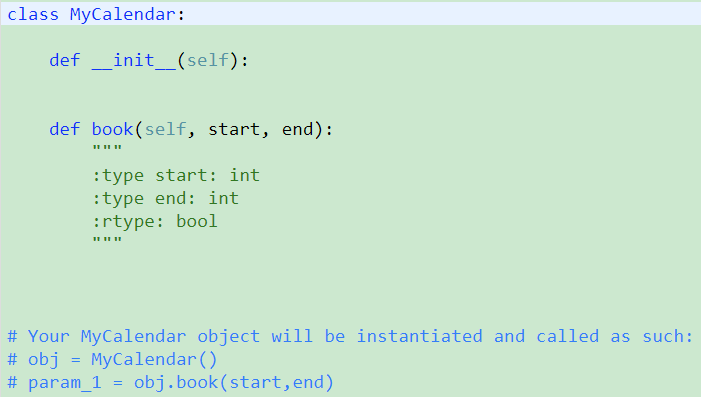
解题思路:
设置interval数组,然后每book一次就对interval数组进行遍历比较,如果没有重合就插入返回True,否则返回False
code: TLE 73 / 108 test cases passed.
1 class MyCalendar: 2 3 def __init__(self): 4 self.interval = [] 5 6 def book(self, start, end): 7 """ 8 :type start: int 9 :type end: int 10 :rtype: bool 11 """ 12 for i in range(len(self.interval)): 13 if self.interval[i][0]<=start<self.interval[i][1] or self.interval[i][0]<end<=self.interval[i][1] or (self.interval[i][0]>start and self.interval[i][1]<end): 14 return False 15 self.interval.append([start,end]) 16 return True 17 18 19 20 # Your MyCalendar object will be instantiated and called as such: 21 # obj = MyCalendar() 22 # param_1 = obj.book(start,end)
看了下答案,同样是暴力搜索,人家技巧就是更高,只改动一句
TLE 108/108 passed
1 class MyCalendar: 2 3 def __init__(self): 4 self.interval = [] 5 6 def book(self, start, end): 7 """ 8 :type start: int 9 :type end: int 10 :rtype: bool 11 """ 12 for i in range(len(self.interval)): 13 if not (self.interval[i][0]>=end or self.interval[i][1]<=start): 14 return False 15 self.interval.append([start,end]) 16 return True 17 18 19 20 # Your MyCalendar object will be instantiated and called as such: 21 # obj = MyCalendar() 22 # param_1 = obj.book(start,end)
再换成tuple 真是有毒,这样就能直接pass 732ms
1 class MyCalendar: 2 3 def __init__(self): 4 self.intervals = [] 5 6 def book(self, start, end): 7 """ 8 :type start: int 9 :type end: int 10 :rtype: bool 11 """ 12 for s,e in self.intervals: 13 if not (start>=e or end<=s): 14 return False 15 self.intervals.append((start,end)) 16 return True 17 18 19 # Your MyCalendar object will be instantiated and called as such: 20 # obj = MyCalendar() 21 # param_1 = obj.book(start,end)
tuple创建速度明显快于list, 遍历速度差不多,唯一缺点就是不可更改
还有,做比较时,能简洁点儿就简洁一点,这样速度会更快一点
还有些别的解法,使用二叉树和红黑树,红黑树在python中需要手动实现,这里就不放了,下面是二叉树的实现,参考的答案
code: 二叉树 378ms 果然快很多
1 class Node: 2 def __init__(self,s,e): 3 self.e = e 4 self.s = s 5 self.left = None 6 self.right = None 7 8 class MyCalendar: 9 10 def __init__(self): 11 self.root = None 12 13 def book_helper(self,s,e,node): 14 if s >= node.e: 15 if node.right: 16 return self.book_helper(s,e,node.right) 17 else: 18 node.right = Node(s,e) 19 return True 20 elif e <= node.s: 21 if node.left: 22 return self.book_helper(s,e,node.left) 23 else: 24 node.left = Node(s,e) 25 return True 26 else: 27 return False 28 29 def book(self, start, end): 30 """ 31 :type start: int 32 :type end: int 33 :rtype: bool 34 """ 35 if not self.root: 36 self.root = Node(start,end) 37 return True 38 return self.book_helper(start,end,self.root) 39 40 # Your MyCalendar object will be instantiated and called as such: 41 # obj = MyCalendar() 42 # param_1 = obj.book(start,end)
731. My Calendar II【Medium】 返回目录
题目:
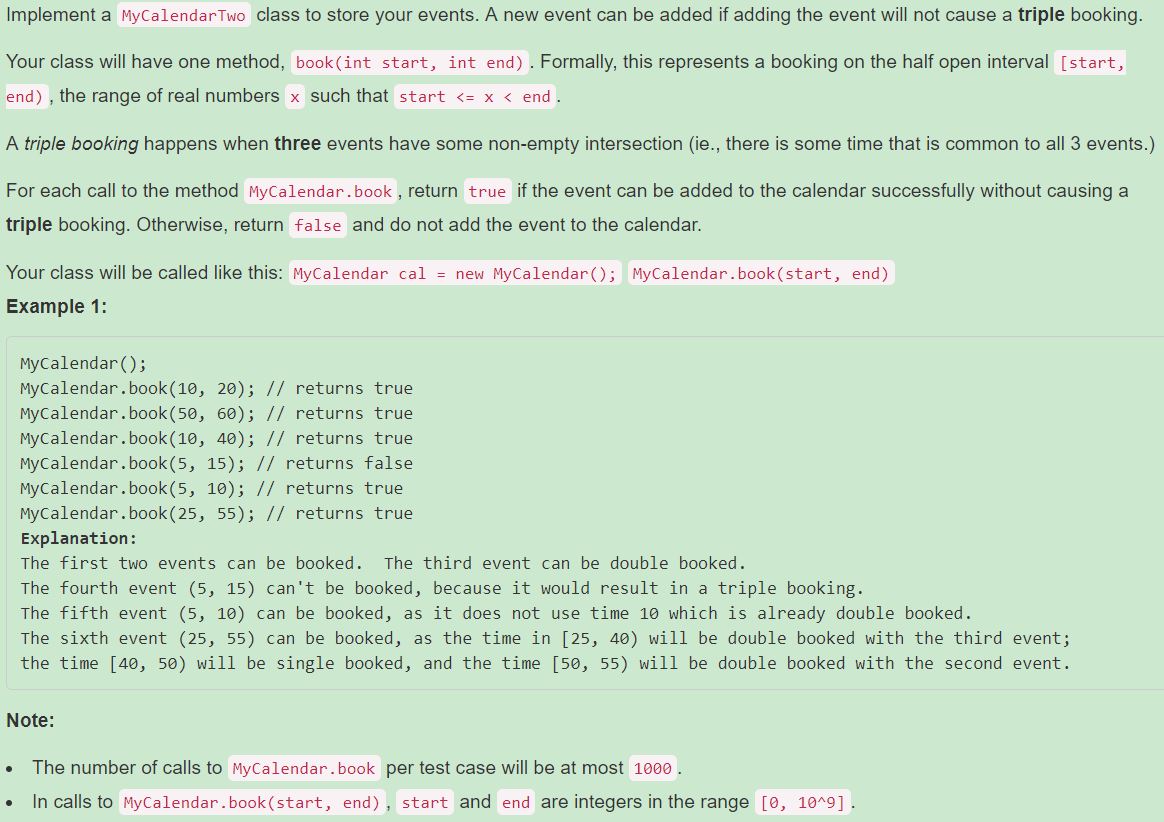
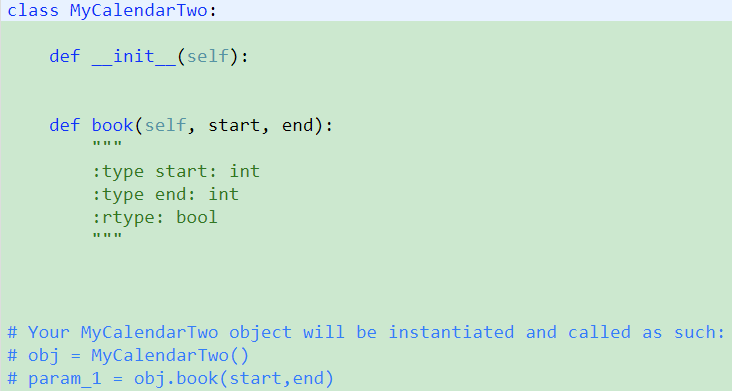
解题思路:
一直想着说用二叉树做,但是对于重合的部分不知道怎么处理,就用三叉树做,用mid节点表示第一次的冲突部分;然后看了下参考答案,直接暴力搜索, 人家写的很简洁巧妙
1 class MyCalendarTwo: 2 3 def __init__(self): 4 self.overlaps = [] 5 self.calendar = [] 6 7 def book(self,start,end): 8 for i,j in self.overlaps: 9 if not (start>=j or end<=i): 10 return False 11 for i,j in self.calendar: 12 if not (start>=j or end<=i): 13 self.overlaps.append((max(start,i),min(end,j))) 14 self.calendar.append((start,end)) 15 return True



